|
||||||||||
31-й Математический Праздник
9 февраля 2020 года
Условия задач
На выполнение заданий отводилось 2 часа (120 минут),
для записи решений школьникам предлагались специальные бланки
(бланк с заданиями 6 класса: blank6.pdf;
7 класса: blank7.pdf).
6 класс
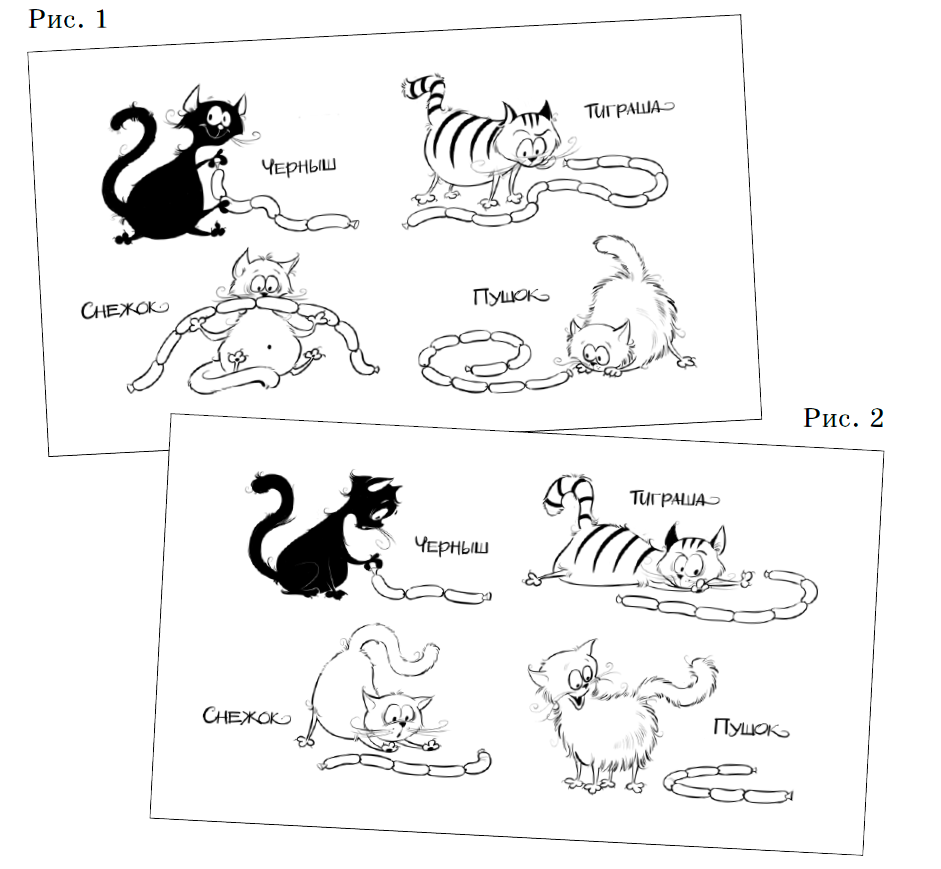
Задача 1. [5 баллов] (Т. И. Голенищева-Кутузова, Т. В. Казицына, А. А. Трунин; художник А.Вайнер)
Таня сфотографировала четырёх котиков, поедающих сосиски (рис. 1).
Вскоре она сделала ещё один
кадр (рис. 2). Каждый котик ест свои сосиски непрерывно
и с постоянной скоростью, а на чужие не покушается. Кто
доест первым и кто последним? Ответ объясните.
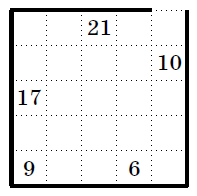
Задача 2. [5 баллов] (М. А. Евдокимов, А. В. Хачатурян)
На клетчатой бумаге был нарисован лабиринт: квадрат 5×5 (внешняя
стена) с выходом шириной в одну клетку, а
также внутренние стенки, идущие по линиям сетки.
На рисунке мы скрыли от вас все
внутренние стенки. Начертите,
как они могли располагаться, зная,
что числа, стоящие в клетках, показывают наименьшее количество шагов,
за которое можно было покинуть лабиринт, стартовав из этой клетки
(шаг делается в соседнюю по стороне клетку, если они не разделены стенкой).
Достаточно одного примера, пояснения не нужны.
Задача 3. [6 баллов] (И. В. Ященко)
На доске написаны числа 2, 3, 4, …, 29, 30.
За рубль можно отметить любое число. Если какое-то число
уже отмечено, можно бесплатно отмечать его делители
и числа, кратные ему. За какое наименьшее число рублей
можно отметить все числа на доске?
Задача 4. [8 баллов] (М. А. Евдокимов, О. А. Заславский, А. В. Шаповалов)
Миша сложил из кубиков куб 3×3×3.
Затем некоторые соседние по грани кубики он склеил друг
с другом. Получилась цельная конструкция из 16 кубиков,
остальные кубики Миша убрал. Обмакнув конструкцию
в чернила, он поочерёдно приложил её к бумаге тремя гранями.
Вышло слово КОТ (см. рис.). Что получится, если
отпечатать грань, противоположную букве «О»?

Задача 5. [8 баллов] (М. А. Хачатурян)
В лесу живёт 40 зверей — лисицы, волки,
зайцы и барсуки. Ежегодно они устраивают бал-маскарад:
каждый надевает маску животного другого вида, причём
два года подряд они одну и ту же маску не носят. Два года
назад на балу было 12 «лисиц» и 28 «волков», год назад — 15 «зайцев»,
10 «лисиц» и 15 «барсуков», а в этом году — 15 «зайцев» и 25 «лисиц».
Каких зверей в лесу больше всего?
Задача 6. [8 баллов] (И. В. Ященко)
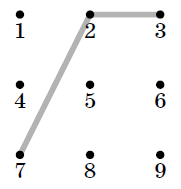
Ваня придумывает число из неповторяющихся цифр
без нулей — пароль для своего телефона. Пароль
работает так: если, не отрывая палец от экрана, последовательно
соединить отрезками точки, соответствующие цифрам пароля,
телефон разблокируется. При этом телефон не
позволяет соединять отрезком две точки, между которыми
есть третья: если Ваня соединит, например, 1 и 3, телефон
«подумает», что Ваня вводит 1-2-3.
Ваня хочет, чтобы при вводе пароля линия движения
пальца не пересекала сама себя. А ещё чтобы перестановкой
цифр пароля ни в каком порядке, кроме обратного,
нельзя было получить другую такую линию. Например,
пароль 1263 Ване не нравится, так как линия
6-3-2-1 другая, но тоже не имеет самопересечений.
Ваня придумал пароль 723 (см. рис.). Эти
три цифры — 2, 3 и 7 — действительно никакой
другой линией соединить нельзя. Жаль
только, что пароль такой короткий.
Помогите Ване придумать пароль подлиннее. В ответе
напишите сам пароль и нарисуйте ту единственную линию,
которую можно получить из этих цифр.
7 класс
Задача 1. [4 балла] (А. А. Заславский, О. А. Заславский)
В ребусе ЯЕМЗМЕЯ=2020 замените
каждую букву в левой части равенства цифрой или знаком
арифметического действия (одинаковые буквы одинаково,
разные — по-разному) так, чтобы получилось верное равенство.
Достаточно привести один пример, пояснений не требуется.
Задача 2. [4 балла]
См. задачу 2 для 6 класса.
Задача 3. [6 баллов] (А. В. Шаповалов)
На столе лежат 6 яблок (не обязательно одинакового веса).
Таня разложила их по 3 на две чашки весов,
и весы остались в равновесии. А Саша разложил те же
яблоки по-другому: 2 яблока на одну чашку и 4 на другую,
и весы опять остались в равновесии. Докажите, что можно
положить на одну чашку весов одно яблоко, а на другую
два так, что весы останутся в равновесии.
Задача 4. [8 баллов] (М. А. Волчкевич)
Три стороны четырёхугольника равны,
а углы четырёхугольника, образованные этими сторонами,
равны 90° и 150°.
Найдите два других угла этого четырёхугольника.
Задача 5. [8 баллов]
См. задачу 5 для 6 класса.
Задача 6. [а) 4 балла; б) 6 баллов] (Ю. С. Маркелов, ученик 10 класса)
Можно ли данную фигуру («верблюда») разбить
а) по линиям сетки;
б) не обязательно по линиям сетки
на 3 части, из которых можно сложить квадрат?

Опубликовано 9 февраля 2020 года







