33-й Математический Праздник в Математической вертикали
27 февраля 2022 года

Условия задач

На выполнение заданий отводилось 2 часа (120 минут).
(PDF-файлы заданий 6 класса: blank-vert6.pdf; 7 класса: blank-vert7.pdf.)

6 класс

Задача 1. [3 балла] (Д. А. Калинин)
Электронные часы показывают время: часы, минуты и секунды, например 18:00:00. Однажды на часах две цифры погасли, и остались только цифры 2, 0, 2, 2 (именно в таком порядке). Назовите самый поздний момент в сутках, когда это могло произойти.

Задача 2. [4 балла] (М. А. Евдокимов)
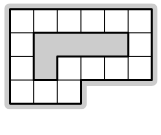
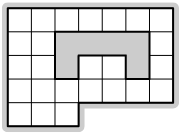
Дана бумажная клетчатая фигура с дыркой (см. рисунок). Покажите, как разрезать эту фигуру на две части таким образом, чтобы из этих частей можно было сложить квадрат. Части можно поворачивать и переворачивать, но нельзя накладывать друг на друга.
а) [2 балла]

б) [2 балла]

Задача 3. [4 балла] (А. В. Шаповалов)
Найдите шестизначное число, у которого первая цифра в 6 раз меньше суммы всех цифр справа от неё и вторая цифра в 6 раз меньше суммы всех цифр справа от неё.

Задача 4. [6 баллов] (А. В. Шаповалов)
Три лягушки сидели на одной прямой. Вначале прыгнула одна из них, потом другая, а затем и третья. Каждая лягушка приземлялась точно в середину отрезка между двумя другими. Оказалось, что длины двух из этих трёх прыжков равны 60 см.
а) [2 балла] Какой могла быть длина оставшегося прыжка?
б) [4 балла] Каким могло быть расстояние между двумя крайними лягушками изначально?

Задача 5. [8 баллов] (Т. В. Казицына)
Лабиринт для мышей (см.рисунок) представляет собой квадрат 5×5 метров, мыши могут бегать только по дорожкам. На двух перекрёстках положили по одинаковому куску сыра (обозначены крестиками). На другом перекрёстке сидит мышка (обозначена кружочком). Она чует, где сыр, но до обоих кусочков ей нужно пробежать одинаковое расстояние. Поэтому она не знает, какой кусочек выбрать, и задумчиво сидит на месте.

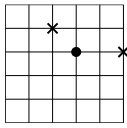
а) [1 балл] Отметьте ещё один перекрёсток, где могла бы задумчиво сидеть мышка (расстояние по дорожкам до обоих кусочков сыра одинаковое).
б) [2 балла] Найдите все 6 перекрёстков, где могла бы сидеть такая мышка (включая найденные ранее).
в) [до 5 баллов] Придумайте, на какие два перекрёстка можно переложить куски сыра так, чтобы подходящих мест для задумчивой мышки оказалось как можно больше.

Задача 6. [8 баллов] (А. А. Заславский)
Цифры от 0 до 9 зашифрованы буквами A, B, C, D, E, F, G, H, I, J в каком-то порядке. За один вопрос можно узнать зашифрованную запись суммы нескольких различных букв. Например, если спросить «А + B = ?», то в случае, когда A = 9, B = 1, C = 0, ответом будет «А + В = BC». Как можно за несколько таких вопросов определить, какие буквы каким цифрам соответствуют? Постарайтесь обойтись как можно меньшим числом вопросов (жюри умеет за 5 вопросов).

7 класс

Задача 1. [4 балла] (В. А. Клепцын)
На рисунке изображены два кодовых замка. Замок откроется, если вписать в кружочки различные цифры так, чтобы число внутри каждого из треугольников совпало или с суммой, или с произведением цифр в его вершинах. Какая комбинация из а) [1 балл] четырёх б) [3 балла] пяти различных цифр откроет замок?

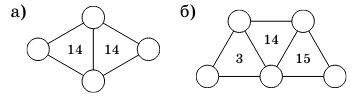
Задача 2.
См. задачу 2 для 6 класса в Математической вертикали.

Задача 3. [4 балла] (И. В. Ященко, И. В. Раскина)
Доктор Айболит хочет навестить и корову, и волчицу, и жучка, и червячка. Все четверо живут вдоль одной прямой дороги. Орлы готовы утром доставить Айболита к первому пациенту, а вечером забрать от последнего, но три промежуточных перехода ему придётся сделать пешком. Если Айболит начнёт с коровы, то длина его кратчайшего маршрута составит 6 км, если с волчицы — 7 км, а если с жучка — 8 км.
Нарисуйте, как могли располагаться домики коровы, волчицы, жучка и червячка (достаточно одного примера расположения).

Задача 4. [6 баллов] (На основе задачи 7.3 Матпраздника 2007 года.)
На быстрой зарядке телефон полностью заряжается за 1 час 20 минут, а на обычной — за 4 часа. Федя поставил полностью разряженный телефон сначала на обычную зарядку, а потом, когда нашёл нужный блок, переставил на быструю до окончания зарядки. Найдите общее время зарядки телефона, если известно, что на быстрой зарядке телефон находился одну треть от общего времени зарядки. Считайте, что и при быстрой, и при обычной зарядке телефон заряжается равномерно.

Задача 5.
См. задачу 5 для 6 класса в математической вертикали

Задача 6. [8 баллов] (Ф. А. Ивлев, А. А. Марданов)
На сторонах AB и BC квадрата ABCD со стороной, равной 10, отмечены точки K и L соответственно так, что AK=CL=3. На отрезке KL выбрали точку P, а на продолжении отрезка AB за точку B выбрали точку Q так, что AP=PQ=QL (см. рис.).

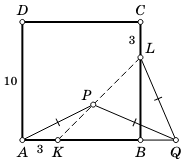
а) [4 балла] Докажите, что ∠PAB=∠BLQ.
б) [4 балла] Найдите длину отрезка BQ. При решении пункта б) можно пользоваться утверждением пункта а).

Опубликовано 27 февраля 2022 года