4-й Математический праздник в Математической вертикали
19 февраля 2023 года

Условия задач

На выполнение заданий отводилось 2 часа (120 минут).
(PDF-файлы заданий 6 класса: blank-vert6.pdf; 7 класса: blank-vert7.pdf.)

6 класс

Задача 1. [4 балла] (М. А. Евдокимов)
Аня называет дату красивой, если все 6 цифр её записи различны. Например, 19.04.23 красивая дата, а 19.02.23 и 01.06.23 нет.
а) [2 балла] Сколько красивых дат будет в апреле 2023 года?
б) [2 балла] Сколько всего красивых дат в 2023 году?

Задача 2. [4 балла] (Т. В. Казицына)
Кот за полминуты съел половинку самой маленькой рыбки, а всего он съел 5 рыбок и потратил на это целое число минут (кот ест рыбу с постоянной в «клеточках» скоростью). На рисунке изображены все рыбки, которые были у кота. Какую рыбку кот не стал есть?

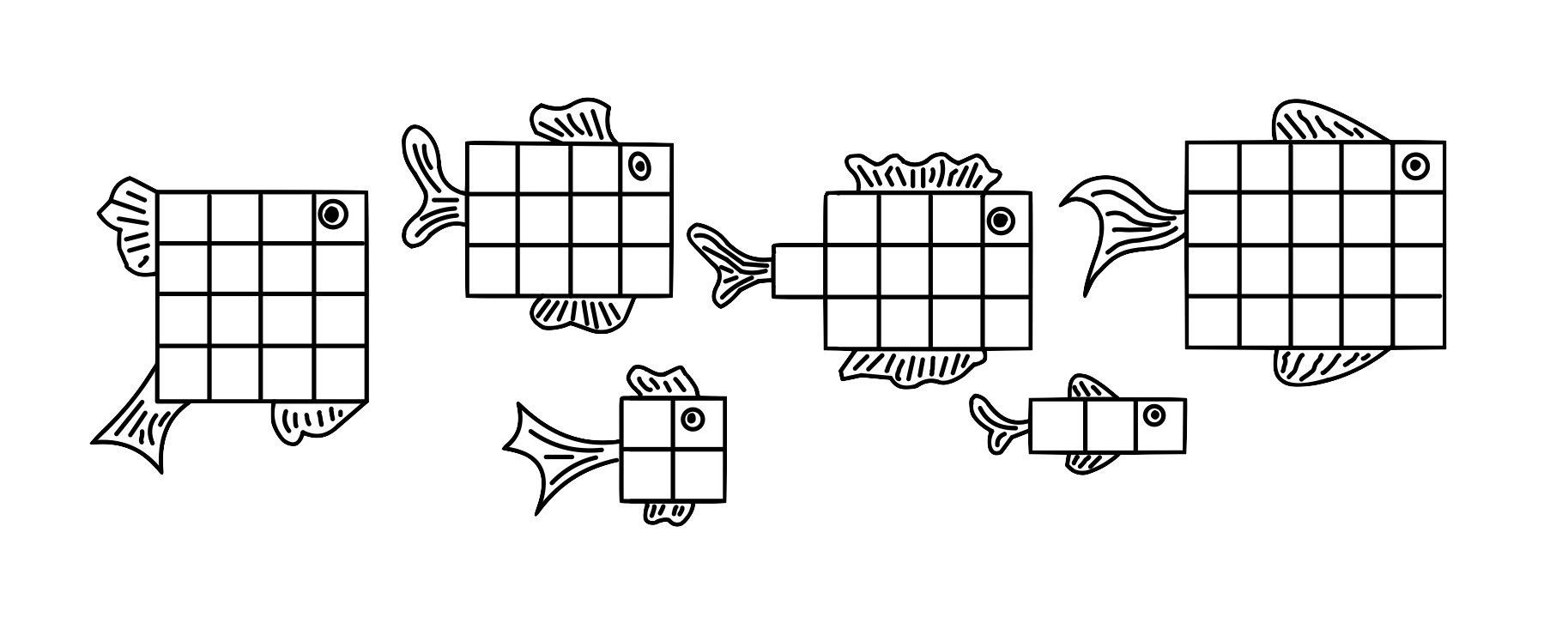
Задача 3. [6 баллов] (Б. Р. Френкин)
Вася в течение 15 дней решал задачи — каждый день хотя бы одну. Каждый день (кроме первого), если погода была пасмурная, то он решал на одну задачу больше, чем в предыдущий день, а если солнечная — на одну задачу меньше. За первые 9 дней Вася решил 13 задач.
а) [4 балла] Какая погода была на 10-й день? Сколько задач он решил в этот день?
б) [2 балла] Какое наибольшее число задач мог решить Вася в 15-й день?

Задача 4. [7 баллов] (А. В. Шаповалов)
Сто сидений карусели расположены по кругу через равные промежутки. Каждое покрашено в жёлтый, синий или красный цвет. Сиденья одного и того же цвета расположены подряд и пронумерованы 1, 2, 3, ... по часовой стрелке. Синее сиденье № 7 противоположно красному № 3, а жёлтое № 7 — красному № 23. Найдите, сколько на карусели жёлтых сидений, сколько синих и сколько красных.

Задача 5. [7 баллов] (Т. И. Голенищева–Кутузова, Т. А. Корчемкина)
а) [2 балла] От маленького «печенья» откусили кусочек. Разрежьте остаток, изображенный на рисунке, на 3 равные части (т. е. одинаковые по размеру и по форме). Разрезы не обязательно прямолинейные.


б) [5 баллов] Разрежьте большое «печенье» на 16 равных частей (т. е. одинаковых по размеру и по форме). Разрезы не обязательно прямолинейные.

Задача 6. [10 баллов] (М. А. Евдокимов)
У царя есть 5 мешков с золотыми монетами, в каждом по 100 монет. Царь помнит, что в одном мешке все монеты весят 10 г, во втором 11 г, в третьем 12 г, в четвёртом 13 г, в пятом 14 г, но не помнит, где какие. Царь сообщил это придворному мудрецу и указал на один из мешков. Мудрец может вынимать из этого и из других мешков любое количество монет, но на вид они все одинаковы. Однако у мудреца есть большие двухчашечные весы без гирь (они точно покажут, равны ли веса на чашках, а если нет, то какая чашка тяжелее).
а) [4 балла] Может ли мудрец за одно взвешивание проверить, верно ли, что в указанном мешке хранятся монеты по 10 г?
б) [6 баллов] Может ли мудрец определить, какие монеты в указанном мешке, сделав не более двух взвешиваний?

7 класс

Задача 1. [4 балла] (Т. В. Казицына)
Дети посетили дельфинарий. Катя запомнила, что там было ровно 7 то ли выдр, то ли тюленей; Юра — что там было ровно 6 то ли морских котиков, то ли тюленей; Игорь — что там было ровно 5 то ли выдр, то ли морских котиков; Серёжа — что меньше всего там было то ли тюленей, то ли выдр. Никто из них не ошибся. Сколько выдр, тюленей и морских котиков было в дельфинарии?

Задача 2. [5 баллов] (Э. А. Акопян)
Найдите какое-нибудь решение ребуса Ф / Е + ВР / АЛЬ = 1. Разным буквам соответствуют разные цифры. Черта обозначает деление.

Задача 3. [6 баллов] (М. А. Евдокимов, Т. В. Казицына)
Ваня сложил куб 3 × 3 × 3 из красных и синих брусков размером 1 × 1 × 3. Затем он начал рисовать то, что у него получилось. Когда пришла Таня, Ваня успел раскрасить лишь 8 из 27 клеток на видимой поверхности нарисованного куба (см. рисунок). Посмотрев на рисунок, Таня сказала, что не знает цвет лишь одной из ещё не раскрашенных клеток. Ваня ответил, что эта клетка — красная. Завершите Ванин рисунок (отметьте буквой «С» синие клетки, буквой «К» красные, знаком «?» клетку, цвет которой Таня не могла восстановить).

Задача 4. [7 баллов] (А. В. Шаповалов)
Сто сидений карусели расположены по кругу через равные промежутки. Каждое покрашено в жёлтый, синий или красный цвет. Сиденья одного и того же цвета расположены подряд и пронумерованы 1, 2, 3, ... по часовой стрелке. Синее сиденье № 7 противоположно красному № 3, а жёлтое № 7 — красному № 23. Найдите, сколько на карусели жёлтых сидений, сколько синих и сколько красных.

Задача 5. [8 баллов] (Л. А. Попов)
Равнобедренный треугольник ABC (AB=BC) и квадрат AKLM расположены, как показано на рисунке. Точка S на AB такова, что AS=SL. Найдите величину угла SLB.

Задача 6. [10 баллов] (М. А. Евдокимов)
У царя есть 7 мешков с золотыми монетами, в каждом по 100 монет. Царь помнит, что в одном мешке все монеты весят 7 г, во втором 8 г, в третьем 9 г, в четвёртом 10 г, в пятом 11 г, в шестом 12 г, в седьмом 13 г, но не помнит, где какие. Царь сообщил это придворному мудрецу и указал на один из мешков. Мудрец может вынимать из этого и из других мешков любое количество монет, но на вид они все одинаковы. Однако у мудреца есть большие двухчашечные весы без гирь (они точно покажут, равны ли веса на чашках, а если нет, то какая чашка тяжелее).
а) [4 балла] Может ли мудрец за одно взвешивание проверить, верно ли, что в указанном мешке хранятся монеты по 7 г?
б) [6 баллов] Может ли мудрец определить, какие монеты в указанном мешке, сделав не более двух взвешиваний?

Опубликовано 19 февраля 2023 года