|
||||||||||
|
|
11-й Математический Праздник.
13 февраля 2000 года
Условия и решения задач.
6 класс
Задача 1. [5 баллов]
В записи *1*2*4*8*16*32*64=27
вместо знаков "*" поставьте знаки "+" или "-" так, чтобы
равенство cтало верным.
Решение.
Знаки можно расставить следующим образом:
+ 1 - 2 + 4 + 8 - 16 - 32 + 64 = 27.
Найти такое расположение знаков легко, если расставлять знаки справа налево.
Ответ: +1-2+4+8-16-32+64=27.
Замечание.
Попробуйте сами доказать, что
а) любое число, получающееся таким способом, нечётно;
б) из этой записи можно получить любое нечётное число между
числами -128 и 128, причём единственным способом.
Задача 2. [4 балла]
В квадрате 7*7 клеток закрасьте некоторые клетки так, чтобы в каждой
строке и в каждом столбце оказалось ровно по 3 закрашенных клетки.
Решение.

На рисунках приведены примеры такой закраски.
На левом рисунке закрашивали клетки, как на шахматной доске,
кроме четырёх клеток на диагонали.
На правом - клетки закрашивали "лесенкой", начиная с
левого нижнего угла.
Замечание.
Способ, приводящий к правому рисунку, помогает при решении многих
подобных задач.
Задача 3. [6 баллов]
Шифр кодового замка является двузначным числом.
Буратино забыл код, но помнит, что сумма цифр этого числа,
сложенная с их произведением, равна самому числу.
Напишите все возможные варианты кода, чтобы
Буратино смог быстрее открыть замок.
Решение.
Пусть первая цифра кода x, а вторая y. Тогда само число
записывается как 10x+y, а условие задачи можно записать
уравнением (x+y)+x*y=10x+y. Следовательно, x*y=9x.
Так как код - двузначное число, то x не равно 0, а значит,
y=9. При этом x можно взять любым, кроме 0. Проверьте!
Ответ: 19, 29, 39, 49, 59, 69, 79, 89, 99.
Задача 4. [8 баллов]
Зачеркните все 13 точек (как на рисунке) пятью отрезками, не
отрывая карандаша от бумаги и не проводя никакую линию дважды.

Решение. Пример приведен на рисунке:

Задача 5. [10 баллов]
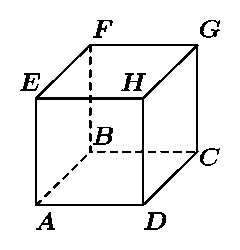
В одной из вершин куба ABCDEFGH сидит заяц, но охотникам он не виден.
Три охотника стреляют залпом, при этом они могут "поразить" любые три вершины
куба. Если они не попадают в зайца, то до следующего залпа заяц перебегает
в одну из трёх соседних (по ребру) вершин куба.
Укажите, как стрелять охотникам, чтобы обязательно попасть в зайца за четыре
залпа.
(В решении достаточно написать четыре тройки вершин, в которые стреляют
охотники.)
Решение. Покрасим вершины A, C, F и H в чёрный цвет, а остальные вершины - в белый. Заметим, что любые две соседние вершины будут покрашены в разные цвета. Значит, после каждого залпа заяц перебегает в вершину другого цвета.
Сделаем первый залп по вершинам C, F и H.
Если заяц находился в чёрной вершине, то либо охотники сразу попали в
него, либо заяц находился в вершине A. В последнем случае после залпа
заяц перебежит в одну из трех соседних вершин, и залп (BDE)
обязательно достигнет цели.
Если заяц находился в белой вершине, то после двух выстрелов он снова окажется в белой вершине. Рассуждая аналогично предыдущему случаю, убеждаемся, что залпы (DEG), а потом (ACF) обязательно поразят зайца.
Ответ: охотники обязательно попадут в зайца, сделав следующие
залпы: (CFH), (BDE), (DEG), (ACF). (Порядок залпов важен!)
Авторы задач:
А. Ю. Митягин (1, 2, 3), В. В. Клепцын (3), А. В. Спивак (5).
Дата последнего изменения: 15 февраля 2000 года







