12-й Математический Праздник.
18 февраля 2001 года

Условия и решения задач.

6 класс

Задача 1 [4 балла].
Решите ребус: АX*УХ=2001.
Автор: А. Блинков
Решение:
2001=3*23*29. Поэтому число 2001 можно представить в виде произведения двузначных чисел лишь следующими способами: 69*29 или 23*87.
Ответ: АХ=29, УХ=69 или наоборот, АХ=69, УХ=29.

Задача 2 [4 балла].
Офеня (Продавец в разнос, коробейник.) купил на оптовом рынке партию ручек и предлагает покупателям либо одну ручку за 5 рублей, либо три ручки за 10 рублей. От каждого покупателя Офеня получает одинаковую прибыль. Какова оптовая цена ручки?
Автор: А. Саблин
Решение:
Если оптовая цена ручки x рублей, то 5-x=10-3x, откуда x=2,5. Значит, оптовая цена - 2 рубля 50 копеек.
Ответ:Оптовая цена ручки - 2 рубля 50 копеек.

Задача 3 [6 баллов].
Наташа и Инна купили по одинаковой коробке чая в пакетиках. Известно, что одного пакетика хватает на две или три чашки чая. Наташе коробки хватило только на 41 чашку чая, а Инне - только на 58. Сколько пакетиков было в коробке?
Авторы: А. Спивак, И. Ященко
Решение 1:
Заметим, что в коробке не могло быть меньше 20 пакетиков: если их хотя бы 19, то Инна не cможет выпить больше 19*3=57 чашек, а она выпила 58. С другой стороны, в коробке не могло быть больше 20 пакетиков: если их хотя бы 21, то Наташа не могла выпить меньше 21*2=42 чашек, а она выпила 41. Тем самым, в коробке было 20 пакетиков: Инна заварила 18 пакетиков по три раза и 2 пакетика по два раза, а Наташа заварила 1 пакетик три раза и 19 пакетиков по два раза.
Замечание
Обязательно надо предъявить способ выпить 41 и 58 чашек чая, иначе решение не будет полным.
Решение 2:
Заметим, что Инна выпила на 17 чашек чая больше, чем Наташа. Это значит, что по крайней мере 17 пакетиков Инна использовала по три раза. Из этих пакетиков она заварила 17*3=51 чашку чая. Кроме этих чашек она выпила еще 58-51=7 чашек чая. Семь чашек чая в условиях задачи можно заварить единственным способом -- 2 пакетика использовать по два раза и 1 пакетик заварить три раза. Таким образом, в коробке было ровно 20 пакетиков чая: Инна заварила 18 пакетиков по три раза и 2 пакетика по два раза, а Наташа заварила 1 пакетик три раза и 19 пакетиков по два раза.
Ответ:В коробке было 20 пакетиков чая.

Задача 4 [6 баллов].
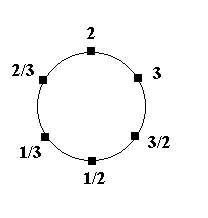
Расставьте по кругу 6 различных чисел так, чтобы каждое из них равнялось произведению двух соседних.
Автор: А. Митягин
Решение:
Если рядом стоят числа a и b, то следующим стоит число b/a, за ним 1/a, потом 1/b, наконец, a/b. Такие шесть чисел удовлетворяют условию задачи. Конечно, при неудачном выборе чисел a и b какие-то из указанных выше шести чисел совпадут, но нас это не остановит: для решения задачи достаточно предъявить один пример. Например, взять a=2, b=3.
Ответ:

Задача 5 [8 баллов].
Вифсла, Тофсла и Хемуль играли в снежки. Первый снежок бросил Тофсла. Затем в ответ на каждый попавший в него снежок Вифсла бросал 6 снежков, Хемуль - 5, а Тофсла - 4. Через некоторое время игра закончилась. Найдите, в кого сколько снежков попало, если мимо цели пролетели 13 снежков. (В себя самого снежками не кидаются.)
Авторы: Т. Голенищева-Кутузова, В. Клепцын
Решение:
Если в Вифслу, Тофслу и Хемуля попали x, y и z снежков соответственно, то всего было брошено 13+x+y+z снежков (поскольку 13 снежков не достигли цели). С другой стороны, Вифсла бросил 6x, Хемуль - 5y, а Тофсла - (4z+1) снежков (вместе с первым снежком). Получаем уравнение: 6x+5y+4z+1=13+x+y+z, откуда 5x+4y+3z=12. Так как x, y, z - целые неотрицательные числа, то x может быть равен 1 или 2, y - 1, 2 или 3, z - 1, 2, 3 или 4. Перебором находим единственное решение (1; 1; 1).
Ответ: В Хемуля, Вифслу и Тофслу попали по одному разу.

Задача 6.
Поля клетчатой доски размером 8*8 будем по очереди закрашивать в красный цвет так, чтобы после закрашивания каждой следующей клетки фигура, состоящая из закрашенных клеток, имела ось симметрии. Покажите, как можно закрасить
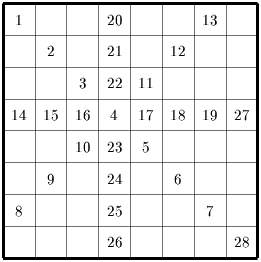
а) [6 баллов] 26;
б) [4 балла] 28 клеток, соблюдая это условие. (В качестве ответа расставьте на тех клетках, которые должны быть закрашены, числа от 1 до 26 или до 28 в том порядке, в котором проводилось закрашивание.)
Автор: И. Акулич
Ответ: