16-й Математический Праздник.
13 февраля 2005 года

Условия и решения задач.

6 класс

На выполнение задания школьникам давалось 2 часа (120 минут).

Задача 1. [3 балла] Таракан Валентин объявил, что умеет бегать со скоростью 50 м/мин. Ему не поверили, и правильно: на самом деле Валентин всё перепутал и думал, что в метре 60 сантиметров, а в минуте 100 секунд. С какой скоростью (в "нормальных" м/мин) бегает таракан Валентин?

Ответ. 18 м/мин.

Решение. Валентин пробегает 50*60=3000 см за 100 с, то есть его скорость 30 см/с, что составляет 18 м/мин.

Задача 2. [3 балла]

На автобусе ездил Андрей
На кружок и обратно домой,
Заплатив 115 рублей,
Покупал он себе проездной.

В январе он его не достал,
И поэтому несколько дней
У шофёра билет покупал
Он себе за 15 рублей.

А в иной день кондуктор с него
Брал 11 только рублей.
Возвращаясь с кружка своего
Всякий раз шёл пешком наш Андрей.

За январь сколько денег ушло,
Посчитал бережливый Андрей:
С удивлением он получил
Аккурат 115 рублей!

Сосчитайте теперь поскорей,
Сколько раз был кружок в январе?

Ответ. 9 раз.

Решение. Количество рублей, потраченных Андреем в те дни, когда он покупал билет у шофёра, делится на 5; на 5 делится и общее количество потраченных им в январе рублей. Значит, и в другие дни общее количество потраченных денег делилось на 5. Поэтому, количество дней, когда Андрей покупал билет у кондуктора, делится на 5. Числа 0 и 10 не годятся; числа, большие 10 - тем более, поэтому единственный воз- можный вариант - 5 дней. Тогда остальных дней (115-11*5)/15=4, а кружок был 9 раз.

Задача 3. Лиса и два медвежонка делят 100 конфет. Лиса раскладывает конфеты на три кучки; кому какая достанется - определяет жребий. Лиса знает, что если медвежатам достанется разное количество конфет, то они попросят её уравнять их кучки, и тогда она заберёт излишек себе. После этого все едят доставшиеся им конфеты.

а) [2 балла] Придумайте, как Лисе разложить конфеты по кучкам так, чтобы съесть ровно 80 конфет (ни больше, ни меньше).

б) [4 балла] Может ли Лиса сделать так, чтобы в итоге съесть ровно 65 конфет?

Ответ. а) 10, 10 и 80; б) нет.

Решение. а) Лиса раскладывает конфеты так: 10, 10 и 80. Если ей достанется кучка из 80 конфет, то медвежатам достанется поровну конфет, и они не будут жаловаться. Если ей достанется кучка из 10 конфет, то, для того чтобы уравнять доли медвежат, ей придётся съесть ещё 70 конфет.

Примечание. Можно показать, что это - единственный способ действия Лисы. В самом деле, поскольку в итоге лиса съест 80 конфет, то медвежата съедят по (100-80)/2=10 конфет. Так как у одного из медвежат количество конфет не менялось, то в кучке, доставшейся ему по жребию, было 10 конфет. Следовательно, какая бы кучка ни досталась Лисе по жребию, среди двух оставшихся обязательно есть кучка из 10 конфет. То есть кучек по 10 конфет по крайней мере две (если бы такая кучка из 10 конфет была лишь одна, то она по жребию могла достаться Лисе, и среди двух оставшихся не нашлось бы кучки из 10 конфет). Следовательно, Лиса может разложить конфеты по кучкам так, чтобы в итоге получить ровно 80 конфет, единственным способом.

б) Покажем, что число конфет, съеденных Лисой, всегда чётно (и поэтому не может быть равным 65). В итоге медвежата съели поровну конфет, поэтому суммарное число конфет, съеденных медвежатами, чётно. Так как 100 - чётное число, то Лиса также съела чётное число конфет.

Задача 4. Незнайка разместил без наложений в квадрате 10*10 только 13 фигур ("скобок"), изображённых на рисунке. Попробуйте разместить больше.

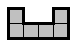
[За каждую скобку сверх тринадцати - 2 балла]

Ответ. Можно разместить 14, 15 или даже 16 "скобок". Больше разместить нельзя, так как 17 "скобок" занимают уже 102 клетки.

Задача 5. [6 баллов] В числах МИХАЙЛО и ЛОМОНОСОВ каждая буква обозначает цифру (разным буквам соответствуют разные цифры). Известно, что у этих чисел произведения цифр равны. Могут ли оба числа быть нечётными?

Ответ. Нет.

Решение. Заметим, что использованы 10 различных букв, поэтому каждая цифра обозначена какой-нибудь буквой, в частности, среди этих цифр есть нуль. Таким образом, произведение цифр одного (а значит, и второго) числа равно нулю. Следовательно, в записи обоих чисел есть нуль. В словах МИХАЙЛО и ЛОМОНОСОВ общие буквы М, Л и О, поэтому нуль обозначает одна из них. Это не могут быть Л и М, поскольку числа не могут начинаться с нуля. Значит, нуль обозначен буквой О. В числе МИХАЙЛО на конце нуль, то есть оно чётное.

Задача 6. В Пустоземье живут три племени: эльфы, гоблины и хоббиты. Эльф всегда говорит только правду, гоблин всегда лжёт, а хоббит через раз говорит то правду, то ложь. Однажды за круглым столом пировало несколько пустоземцев, и один из них сказал, указав на своего левого соседа: "Он - хоббит". Сосед сказал: "Мой правый сосед солгал". В точности ту же фразу затем повторил его левый сосед, потом её же произнёс следующий по кругу, и так они говорили "Мой правый сосед солгал" много-много кругов, да и сейчас ещё, возможно, говорят.
Определите, из каких племён были пирующие, если известно, что за столом сидело
а) [4 балла] девять;
б) [4 балла] десять
жителей Пустоземья. Объясните своё решение.

Ответ. а) Все были хоббитами; б) пять гоблинов и пять эльфов.

Решение. Рассмотрим того, про кого сказали, что он - хоббит, и для удобства назовём его Боб. Боб не согласился с тем, что он хоббит, следующий не согласился с ним, а значит, подтвердил, что Боб хоббит, и так далее - все говорящие через раз подтверждали или отрицали, что Боб хоббит. Если пирующих было 9 (нечётное число), то на следующем круге каждый говорил противоположное к тому, что сказал на предыдущем, так что все они хоббиты, а первый хоббит про Боба сказал сначала правду, что вполне возможно. Мы решили пункт а) задачи. Для решения пункта б) заметим, что, поскольку 10 - чётное число, то говорящие на каждом круге говорят одно и то же, поэтому хоббитов среди них нет. Тогда и Боб - не хоббит, а сказавший так про него его правый сосед солгал, то есть он гоблин. Сам же Боб уличил гоблина во лжи, так что он эльф. Его сосед слева снова гоблин, и так далее - за столом сидят, чередуясь, пять гоблинов и пять эльфов.

Дата последнего изменения — 13 февраля 2005 года