17-й Математический Праздник.
12 февраля 2006 года

Условия и решения задач.

6 класс

На выполнение задания школьникам давалось 2 часа (120 минут).

Задача 1. Доктор Айболит раздал четырём заболевшим зверям 2006 чудодейственных таблеток. Носорог получил на одну больше, чем крокодил, бегемот на одну больше, чем носорог, а слон - на одну больше, чем бегемот. Сколько таблеток придётся съесть слону? [3 балла]

Ответ. 503 таблетки.

Решение. Пока звери не съели лекарство, заберём одну таблетку у носорога, две у бегемота и три у слона. Теперь у всех четверых поровну. Забрали мы 6 таблеток, то есть осталось их 2000 - по 500 у каждого. У слона забрали 3 таблетки, то есть Айболит прописал слону 503 таблетки.

Задача 2. Разрежьте фигуру (см. первый рисунок) на две одинаковые (совпадающие при наложении) части. [4 балла]

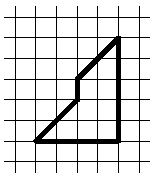
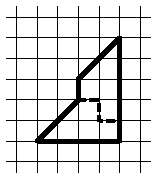
Ответ. Искомый разрез показан на втором рисунке.

Задача 3. Саша пригласил Петю в гости, сказав, что живёт в 10-м подъезде в квартире N 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На какой этаж ему следует подняться? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.) [5 баллов]

Ответ. На 3-й этаж.

Решение. Если на этаже не более трёх квартир, то в десяти подъездах их не более, чем 10*9*3=270, то есть в 10-м подъезде квартиры N 333 не будет. Если на этаже не менее пяти квартир, то уже в девяти подъездах будет не менее, чем 9*9*5=405 квартир, то есть искомая квартира будет не в десятом подъезде. Значит, квартир на этаже 4, в первых девяти подъездах 9*9*4=324 квартиры. Тогда в десятом подъезде квартиры начинаются с 325-й. На втором этаже они начнутся с 329-й, на третьем - с 333-й. Таким образом, Пете нужно подняться на третий этаж.

Задача 4. Таня стоит на берегу речки. У неё есть два глиняных кувшина: один - на 5 литров, а про второй Таня помнит лишь то, что он вмещает то ли 3, то ли 4 литра. Помогите Тане определить ёмкость второго кувшина. (Заглядывая в кувшин, нельзя понять, сколько в нём воды.) [5 баллов]

Решение. Первый способ. Пусть Таня нальёт из полного малого кувшина речную воду в большой, а затем наполнит малый и из него дольёт большой доверху. Далее Тане надо опорожнить большой сосуд и вылить в него остаток из малого. Если малый был на 3 литра, то сейчас в большом 1 литр, иначе - 3 литра. Теперь пусть Таня снова попытается перелить воду из полного малого кувшина в большой. Если это ей удастся, то малый был трёхлитровым, если вода польётся через край, - четырёхлитровым.

Второй способ. Если бы у Тани большой кувшин вмещал 10 литров, то достаточно было бы попытаться налить в него воду из малого трижды. Если вода польётся через край, то малый на 4 литра, если нет, то на 3. С пятилитровым кувшином такая проверка возможна, если Таня опорожнит пятилитровый кувшин, когда тот заполнится.

Задача 5. Дед звал внука к себе в деревню: "Вот посмотришь, какой я необыкновенный сад посадил! У меня там растёт четыре груши, а ещё есть яблони, причём они посажены так, что на расстоянии 10 метров от каждой яблони растёт ровно две груши". - "Ну и что тут интересного, - ответил внук. - У тебя всего две яблони". "Авот и не угадал, - улыбнулся дед. - Яблонь у меня в саду больше, чем груш". Нарисуйте, как могли расти яблони и груши в саду у деда. Постарайтесь разместить на рисунке как можно больше яблонь, не нарушая условий. Если Вы ду- маете, что разместили максимально возможное число яблонь, попробуйте объяснить, почему это так. [9 баллов]

Решение. Возможны различные расстановки яблонь и груш, например, такая, как показана на первом рисунке. Наибольшее число яблонь можно поместить, если груши растут достаточно густо. Например, если посадить груши в ряд через 5 метров, то найдётся место для 12 яблонь (см. второй рисунок).

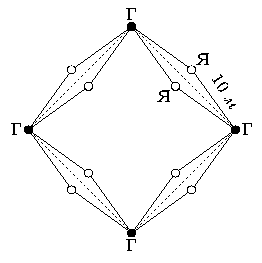
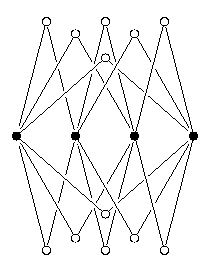
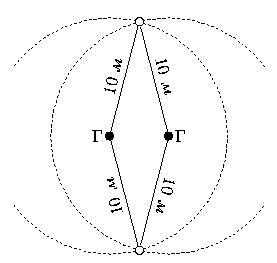
Докажем, что больше двенадцати яблонь быть не может. В самом деле, рассмотрим две какие-то груши. На расстоянии 10 метров от них может быть только две яблони - одна по одну сторону от линии груш, другая - по противоположную (см. третий рисунок). Поэтому каждая пара груш "обслуживает" не более чем две яблони. Так как пар груш ровно шесть (пересчитайте!), то максимальное число яблонь равно 12.

Задача 6. Пять футбольных команд провели турнир - каждая команда сыграла с каждой по разу. За победу начислялось 3 очка, за ничью - 1 очко, за проигрыш очков не давалось. Четыре команды набрали соответственно 1, 2, 5 и 7 очков. А сколько очков набрала пятая команда? [8 баллов]

Решение. Каждая команда провела 4 игры. Ясно, что первая команда один раз сыграла вничью, а остальные игры проиграла. Вторая имеет две ничьи и два поражения. Третья команда пять очков на одних ничьих набрать не могла, стало быть, она один раз выиграла, кроме того, у неё две ничьи и поражение. Четвёртая команда победила два раза (если бы один, то ей пришлось бы набрать в трёх играх на одних ничьих 4 очка, что невозможно). Также у этой команды есть ничья и поражение. В итоге первые четыре команды выиграли 3 раза, а проиграли 7 раз. Однако число побед должно равняться числу поражений. Значит, 4 раза они проиграли пятой команде, и у той 12 очков. Нетрудно привести пример турнира, где такое распределение очков возможно. Пусть пятая команда выиграла у всех, четвёртая - у первой и второй, третья - у первой, а все остальные игры закончились вничью. Тогда у каждой команды будет названное число очков.

Дата последнего изменения — 12 февраля 2006 года