18-й Математический Праздник.
11 февраля 2007 года

Условия и решения задач.

6 класс

На выполнение задания школьникам давалось 2 часа (120 минут).

Задача 1. По двум телевизионным каналам одновременно начали показывать один и тот же фильм. На первом канале фильм разбили на части по 20 минут каждая и вставили между ними двухминутные рекламные паузы. А на втором канале фильм разбили на части по 10 минут каждая и вставили между ними минутные рекламные паузы. На каком канале фильм закончится раньше? [4 балла]

Ответ. На первом канале.

Решение. На первом канале между началом каждой части и началом следующей проходит 22 минуты. За это время на втором канале пройдут две части по 10 минут и две минутные рекламные паузы. Следовательно, началу каждой части на первом канале соответствует тот же момент фильма на втором.

Когда на первом канале начнётся последняя часть, до конца фильма останется 20 минут, рекламы уже не будет. На втором же канале покажут две части по 10 минут с минутной рекламной паузой, поэтому на первом канале фильм закончится на одну минуту раньше.

Задача 2. В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторыми из них знак умножения. Произведение получившихся чисел оказалось равным 2007. Какая отметка выходит у Вовочки в четверти по пению? ("Колов" учительница пения не ставит.) [4 балла]

Ответ. Тройка.

Решение. Разложим число 2007 на простые множители:

2007=3*3*223.

Отсюда можно было бы сделать вывод, что отметки Вовочки - это две двойки и три тройки. Но на самом деле надо ещё доказать, что нет других вариантов отметок. Посмотрим, как ещё можно разложить 2007 на множители: 2007=9*223=3*669. Поскольку отметки 9 не бывает, эти разложения числа 2007 не могли возникнуть из Вовочкиных отметок. Так как троек у Вовочки больше, чем двоек, и последняя отметка, как ни переставляй множители, - тройка, можно надеяться, что тройку в четверти он получит.

Задача 3. Волк с тремя поросятами написал детектив "Три поросёнка--2", а потом вместе с Красной Шапочкой и её бабушкой кулинарную книгу "Красная Шапочка-2". В издательстве выдали гонорар за обе книжки поросёнку Наф-Нафу. Он забрал свою долю и передал оставшиеся 2100 золотых монет Волку. Гонорар за каждую книгу делится поровну между её авторами. Сколько денег Волк должен взять себе? [5 баллов]

Ответ. 700 золотых монет.

Решение. За книгу "Три поросёнка-2" каждый автор должен получить четверть гонорара. Но так как Наф-Наф свою долю уже забрал, Волку причитается 1/3 остатка. За книгу "Красная шапочка-2" ему также полагается 1/3 гонорара. Поэтому всего он должен получить треть переданной ему суммы.

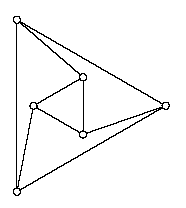
Задача 4. В Совершенном городе шесть площадей. Каждая площадь соединена прямыми улицами ровно с тремя другими площадями. Никакие две улицы в городе не пересекаются. Из трёх улиц, отходящих от каждой площади, одна проходит внутри угла, образованного двумя другими. Начертите возможный план такого города. [6 баллов]

Решение. План города может быть, например, таким, как на рисунке.

Задача 5. Нарисуйте, как из данных трёх фигурок, использовав каждую ровно один раз, сложить фигуру, имеющую ось симметрии. [7 баллов]

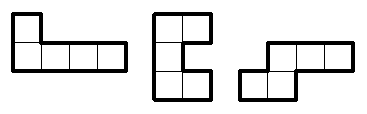
Решение. Из предложенных фигурок можно сложить четыре различные фигуры, имеющие ось симметрии. Две из них приведены на рисунке. У одной из них ось симметрии вертикальная, а у другой проходит по диагонали. Это не случайно - ось симметрии фигуры, нарисованной по клеточкам, может быть либо параллельна сторонам клеток, либо идти под углом 45 градусов к ним.

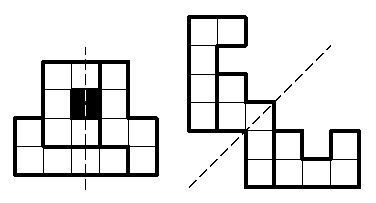
Попробуйте найти остальные два решения.

Задача 6. Кощей Бессмертный похитил у царя трёх дочерей. Отправился Иван-царевич их выручать. Приходит он к Кощею, а тот ему и говорит:

"Завтра поутру увидишь пять заколдованных девушек. Три из них - царевы дочери, а ещё две - мои. Для тебя они будут неотличимы, а сами друг дружку различать смогут. Я подойду к одной из них и стану у неё спрашивать про каждую из пятерых: "Это царевна?". Она может отвечать и правду, и неправду, но ей дозволено назвать царевнами ровно двоих (себя тоже можно называть). Потом я так же опрошу каждую из остальных девушек, и они тоже должны будут назвать царевнами ровно двоих. Если после этого угадаешь, кто из них и вправду царевны, отпущу тебя восвояси невредимым. А если ещё и догадаешься, которая царевна старшая, которая средняя, а которая младшая, то и их забирай с собой."

Иван может передать царевнам записку, чтобы научить их, кого назвать царевнами. Может ли он независимо от ответов Кощеевых дочерей:
а) вернуться живым [4 балла];
б) увезти царевен с собой? [5 баллов]?

Ответ. а) да; а) да.

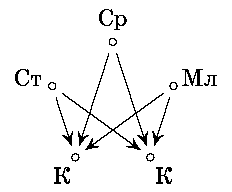
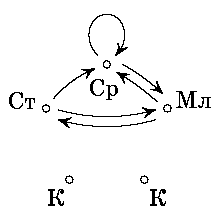
Решение. а) Пусть все царевны назовут царевнами Кощеевых дочек (см. рис). Тогда Кощеевых дочек назовут не менее трёх раз, а царевен - не более чем дважды. Так Иван их и отличит.

Любое из решений пункта б), конечно, годится и для пункта а).

б) Первое решение. Пусть старшая дочь назовёт царевнами среднюю и младшую, младшая - среднюю и старшую, а средняя - себя и младшую (см. рис. 3, снизу). Тогда Иван сразу узнает среднюю царевну - это единственная девушка, которая назвала царевной себя, и её назвали царевной по крайней мере ещё две девушки. После этого Иван узнает младшую царевну (её назвала средняя), а потом и старшую (её назвала младшая). Заметим, что Иван мог бы рассуждать и иначе. Три царевны называют друг друга по кругу: образуют "треугольник", в котором каждая девушка называет следующую. Поскольку ни одна из них не называет царевной дочерей Кощея, а тех всего две, то дочери Кощея не могут входить ни в какой подобный "треугольник". Так можно понять, какие из девушек царевны. Потом, используя остальные ответы, нетрудно установить и старшинство.

Второе решение. Пусть та царевна, которая будет отвечать Кощею первой, назовёт среднюю и младшую царевен, вторая по счёту - старшую и младшую, последняя - старшую и среднюю. Тогда дочери Кощея - те две девушки, которых не назвали трое остальных. Ошибки быть не может, ведь каждую царевну называют как минимум двое. Теперь Иван знает, кто царевны, а старшинство определяется без труда.

Опубликовано 11 февраля 2007 года