|
||||||||||
|
|
11-й Математический Праздник.
13 февраля 2000 года
Условия и решения задач.
7 класс
Задача 1. [3 балла]
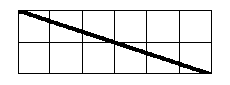
В квадрате 7*7 клеток закрасьте некоторые клетки так, чтобы в каждой
строке и в каждом столбце оказалось ровно по 3 закрашенных клетки. [3 балла]
Смотрите решение задачи N 2 в варианте 6 класса.
Задача 2.
Карлсон написал дробь 10/97. Малыш может:
1) прибавлять любое натуральное число к числителю и знаменателю одновременно,
2) умножать числитель и знаменатель на одно и то же натуральное число.
Сможет ли Малыш с помощью этих действий получить дробь,
а) равную 1/2? [2 балла]
б) равную 1? [4 балла]
Решение.
а) Да, достаточно прибавить к числителю и знаменателю по 77.
(К этому числу приводит уравнение 2(10+x)=97+x.)
б) Нет. Действительно, дробь равна единице, если
ее числитель и знаменатель равны. А Малыш никак не сможет из
неравных чисел сделать равные.
Задача 3.
Дан прямоугольный треугольник. Приложите к нему какой-нибудь треугольник
(эти треугольники должны иметь общую сторону, но не должны
перекрываться даже частично) так, чтобы получился треугольник с двумя
равными сторонами.
Укажите (нарисуйте!) несколько различных решений.
Каждое новое решение - [1 балл].
Решение.
На рисунке цифрами отмечены вершины семи приложенных треугольников.
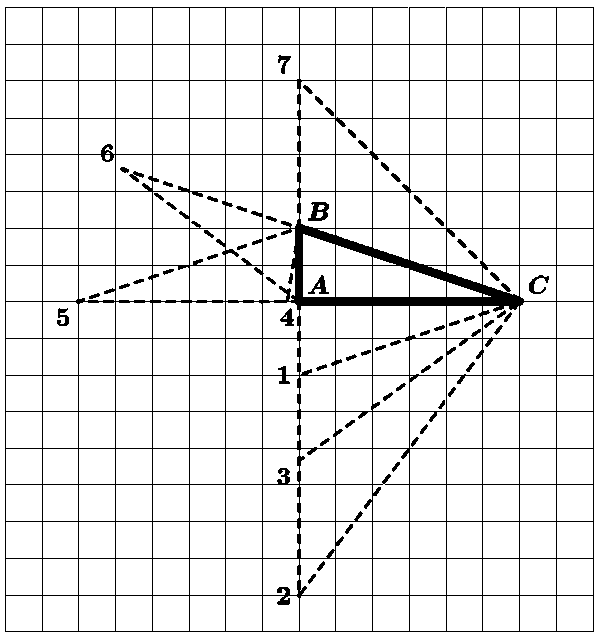
Найдите сами, какие стороны получаются равными.
Задача 4. [8 баллов]
Может ли произведение двух последовательных натуральных чисел равняться
произведению двух последовательных чётных чисел?
Ответ: Нет, не может.
Решение.
Докажем методом от противного.
Предположим, что найдутся два натуральных числа k и n такие, что
n(n+1)=2k(2k+2). Отметим числа 2k и 2k+2 на числовой оси и рассмотрим два
случая: n<2k и n>2k.
Если n<2k, то n+1<2k+2, поэтому
n(n+1)<2k(2k+2). Противоречие.
Если n>2k, то n+1>2k+2, поэтому
n(n+1)>2k(2k+2). Противоречие.
Задача 5. [10 баллов]
В вершинах куба ABCDEFGH расставлены натуральные числа так, что
числа в соседних (по ребру) вершинах отличаются не более чем
на единицу. Докажите, что обязательно найдутся две диаметрально
противоположные вершины, числа в которых отличаются не более чем
на единицу.
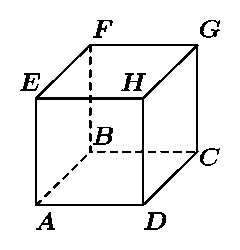
(Пары диаметрально противоположных вершин куба:
A и G, B и H, C и E, D и F.)
Решение.
Обозначим числа, стоящие в вершинах куба,
соответствующими маленькими латинскими буквами:
a, b, c, d, e, f, g и h.
Рассмотрим наименьшее из этих чисел. Без ограничения общности мы можем
считать, что это число a (оно находится в вершине A). Тогда числа в
соседних с A вершинах (это вершины B, D и E) могут принимать
только значения a или a+1 (так как a-1<a). Значит, какие-нибудь
два из чисел b, d и e равны.
Пусть равные числа стоят в вершинах B и E (остальные случаи
рассматриваются аналогично). В этом случае ответом будут диаметрально
противоположные вершины E и C: e=b, а числа c и b отличаются не более,
чем на 1, поэтому числа e и c отличаются не более, чем на 1.
Авторы задач:
А. Ю. Митягин (1), В. В. Клепцын (2), А. Шень (3),
В. В. Произволов (4), Г. А. Гальперин (5)
Дата последнего изменения: 15 февраля 2000 года







