|
||||||||||
|
|
12-й Математический Праздник.
18 февраля 2001 года
Условия и решения задач.
7 класс
Задача 1 [4 балла].
В книге рекордов Гиннесса написано, что наибольшее известное
простое число равно 23021377-1. Не опечатка ли это?
Автор: С. Маркелов
Ответ: Конечно, это опечатка.
Решение
Любая степень числа, оканчивающегося цифрой 1, тоже
оканчивается цифрой 1. Поэтому разность 23021377-1
оканчивается на 0 и, следовательно, не является простым числом.
На самом деле наибольшим известным сегодня простым числом
является число 23021377-1. Простые числа вида 2n-1
называют числами Мерсенна (по имени математика 17 века
М. Мерсенна, который их исследовал). Можно доказать, что при
составном n число 2n-1 составное. Поэтому числа Мерсенна
соответствуют простым n. Например, 22-1=3, 25-1=31,
27-1=127... - простые числа. Однако нельзя утверждать,
что каждому простому числу p соответствует простое
число 2р-1. Например, 211-1 - составное. Поиском чисел
Мерсенна занимались многие выдающиеся математики, например, Эйлер
доказал, что число 231-1 - простое. Конечно или бесконечно
их множество - вопрос, на который пока нет ответа.
Задача 2 [5 баллов].
Приходя в тир, игрок вносит в кассу 100 руб.
После каждого удачного выстрела количество его денег
увеличивается на 10%, а после каждого промаха - уменьшается
на 10%. Могло ли после нескольких выстрелов выстрелов у
него оказаться 80 рублей 19 копеек?
Автор: И. Ященко
Ответ: Да, могло, если он попал только один раз, а три раза промахнулся.
Решение
Решение проще всего найти, если разложить 8019 на множители: 8019=9*9*9*11.
Задача 3 [7 баллов].
Для постройки типового дома не хватало места. Архитектор
изменил проект: убрал 2 подъезда и добавил 3 этажа. При этом
количество квартир увеличилось. Он обрадовался и решил убрать еще
2 подъезда и добавить еще 3 этажа. Могло ли при этом квартир
стать даже меньше, чем в типовом проекте? (В каждом подъезде
одинаковое число этажей, и на всех этажах во всех подъездах одинаковое
число квартир.)
Авторы: В. Гуровиц, И. Ященко
Ответ: Да, могло. Например, если в исходном проекте было 4 подъезда, 1 этаж и на каждом этаже по одной квартире: 4*1=4, 2*3=6, 0*5=0.
Задача 4 [10 баллов].
В стене имеется маленькая дырка (точка). У хозяина есть флажок
следующей формы (см. рисунок):
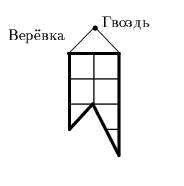
Покажите на рисунке все точки, в которые можно вбить гвоздь, так, чтобы флажок закрывал дырку.
Автор: А. Шень
Ответ:

Задача 5 [10 баллов].
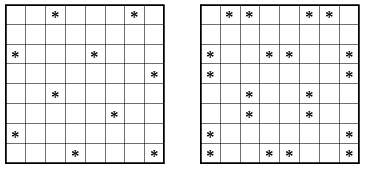
Отметьте на доске 8*8 несколько клеток так, чтобы любая
(в том числе и любая отмеченная) клетка граничила по стороне
ровно с одной отмеченной клеткой.
Автор: А. Спивак
Решение
Будем рассуждать, используя шахматную доску.
Заметим, что белые клетки граничат по стороне только с черными и
наоборот. Поэтому сначала отметим несколько белых клеток так, чтобы у
каждой черной клетки был ровно один отмеченный сосед (на рисунке
слева). Затем отметим несколько черных клеток, чтобы и у каждой белой
клетки появился отмеченный сосед (на рисунке справа), при этом у
черных клеток новых отмеченных соседей не появится.
Ответ:
Дата последнего изменения: 22 февраля 2001 года







