13-й Математический Праздник.
17 февраля 2002 года

Условия и решения задач.

7 класс

Задача 1 [5 балла].
2002 год --- год-палиндром, то есть одинаково читается справа налево и слева направо. Предыдущий год-палиндром был 11 лет назад (1991). Какое максимальное число годов-непалиндромов может идти подряд (между 1000 и 9999 годами)?
Авторы: Г. Гальперин, Д. Григоренко
Решение:
Пусть сейчас год-палиндром, имеющий вид abba. Когда наступит следующий такой год? Рассмотрим два случая:
а) b=9 (год вида a99a). Тогда через 11 лет наступит ещё один год-палиндром: (a+1)00(a+1). Например, годы 3993 и 4004.
б) b<9. В этом случае следующий год-палиндром наступит через 110 лет: a(b+1)(b+1)a.
Например, годы 9339 и 9449. Поэтому наибольшее число годов-непалиндромов подряд - 109.
Примечание: стоящие подряд жирные цифры и буквы, а также выражения в жирных скобках следует считать цифрами числа, а не сомножителями.
Ответ: 109 лет.

Задача 2 [5 баллов].
Незнайка разрезал фигуру на трёхклеточные и четырёхклеточные уголки, нарисованные справа от неё. Сколько трёхклеточных уголков могло получиться?
Автор: А. Митягин

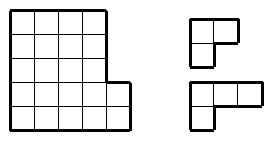
Решение:
Фигура состоит из 22 клеток. Если при разрезании получилось x трёхклеточных уголков и y четырёхклеточных, то 3x+4y=22.
  Очевидно, что число x чётно и x<8 (3*8=24), так что x может быть равно 0, 2, 4 или 6. Ни 0, ни 4 не подходят: y должно быть целым. При x=2 получаем y=4, а при x=6 получаем y=1.
  Оба случая возможны, как показано на рисунках:

x=2		x=6

Ответ: 2 или 6.

Задача 3 [5 баллов].
В написанном на доске примере на умножение хулиган Петя исправил две цифры. Получилось 4*5*4*5*4=2247. Восстановите исходный пример и объясните, как Вы это сделали. Автор: И. Ященко
Решение
В получившемся примере три сомножителя чётные, значит, в исходном примере хотя бы один тоже был чётным. Поэтому и произведение было чётным числом, то есть последняя цифра произведения была изменена. Таким образом, слева изменено не более одной цифры. Значит, в исходном примере слева были и пятёрки, и четвёрки, а оканчивалось произведение на 0.
  Запись числа 4*5*4*5*4=1600 отличается от записи 2240 более чем на одну цифру. Из этого можно заключить, что один из сомножителей исправлен. Если исправлена четвёрка, то произведение должно делиться на 4²*5²=400, а 2240 на 400 не делится, так что исправлена одна из пятёрок.
Ответ: 4*5*4*7*4=2240 (или 4*7*4*5*4=2240).

Задача 4 [5 баллов].
У Васи есть пластмассовый угольник (без делений) с углами 30^o, 60^o и 90^o. Ему нужно построить угол в 15^o. Как это сделать, не используя других инструментов?
Автор: М. Панов
Решение:
Приводим два возможных решения (без сомнения, есть много других):

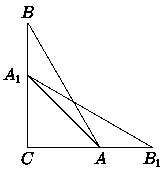/A1AB - искомый		/A1BD=/ABD - искомый

Задача 5.
Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 8*8, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна - ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 36 клеток. Побейте его рекорд!

(За 39 клеток - [2 балла], за каждую следующую клетку - ещё [по 2 балла]. Жюри умеет закрашивать 42 клетки!)
Автор: И. Акулич
Решение:
Пример изображён на рисунке. (Существуют и другие примеры закрашивания 42 клеток. Закрасить 43 клетки невозможно.

Задача 6.
В шахматном турнире на звание мастера спорта участвовало 12 человек, каждый сыграл с каждым по одной партии. За победу в партии даётся 1 очко, за ничью - 0,5 очка, за поражение - 0 очков. По итогам турнира звание мастера спорта присваивали, если участник набрал более 70% от числа очков, получаемых в случае выигрыша всех партий. Могли ли получить звание мастера спорта
а) 7 участников [4 балла];
б) 8 участников [6 баллов]?
Автор: Е. Иванова
Решение:
Докажем от противного, что получить звание мастера могли не более 7 участников турнира. Пусть их было 8. Тогда каждый набрал не менее 0,7*11=7,7 очка, то есть не менее 8 очков. Таким образом, все они в сумме набрали не менее 8*8=64 очков. При этом в партиях с участниками, не получившими звание мастера, каждый из них набрал не более 4 очков (даже если выиграл все партии). Это даёт не более 4*8 = 32 очков.
  Значит, участники, ставшие мастерами, должны были набрать в партиях между собой не менее 32 очков.
  Подсчитаем, сколько партий сыграли между собой эти 8 мастеров. Если мы будем результаты партий записывать в таблицу 8*8, то у нас останется свободной диагональ (так как партий с самим собой не играется) и на каждую партию будет выделено по две клетки: в строке одного из игроков и в строке другого. Таким образом, партий будет (8*8-8)/2=28. В каждой партии разыгрывается одно очко, поэтому в этих партиях мастера в сумме наберут ровно 28 очков, что меньше 32. Противоречие.
  Если же звание мастера получили 9 или более участников, то они должны были набрать не менее 72 очков, в то время как всего в турнире разыгрывалось (12*11)/2=66 очков. Теперь приведём пример турнира, в котором звание мастера получили 7 участников. Пусть первые 7 (по списку) участников всегда выигрывали у последних 5, а все остальные партии завершились вничью. Тогда первые 7 участников набрали по 1*5+0,5*6=8 очков, а последние 5 - по 0*7+0,5*4=2 очка.

Дата последнего изменения: 21 февраля 2002 года