14-й Математический Праздник.
16 февраля 2003 года

Условия и решения задач.

7 класс

Задача 1. [4 балла]
Расставьте скобки и знаки арифметических действий так, чтобы получилось верное равенство:

Задача 2. [6 баллов]
Квадратную салфетку сложили пополам, полученный прямоугольник сложили пополам еще раз. Получившийся квадратик разрезали ножницами (по прямой). Могла ли салфетка распасться
а) на 2 части?
б) на 3 части?
в) на 4 части?
г) на 5 частей?
Если да — нарисуйте такой разрез, если нет — напишите слово "нельзя".

а)
б)
в)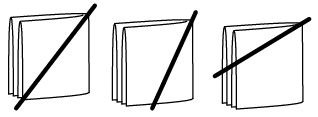
г)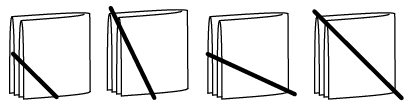

Задача 3. [5 баллов]
Чтобы открыть сейф, нужно ввести код — число, состоящее из семи цифр: двоек и троек. Сейф откроется, если двоек больше, чем троек, а код делится и на 3, и на 4. Придумайте код, открывающий сейф.
Ответ. 2222232.
Решение. Так как двоек больше, чем троек, двоек может быть 4, 5, 6 или 7. В первом случае сумма цифр — 17, во втором — 16, в третьем — 15, а в последнем — 14. По признаку делимости на 3 число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Значит, годится только третий вариант.
Итак, в коде 6 двоек и 1 тройка. По признаку делимости на 4 число, образованное последними двумя цифрами, должно делиться на 4. Значит, это 32.

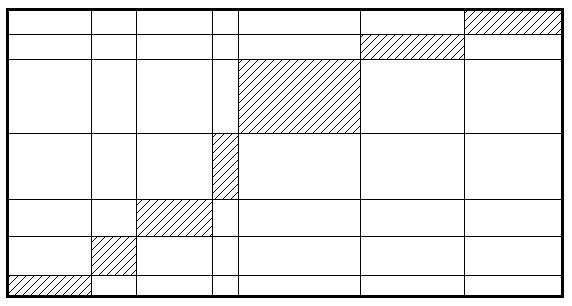
Задача 4. [8 баллов] Прямоугольник разрезали шестью вертикальными и шестью горизонтальными разрезами на 49 прямоугольников (см. рисунок). Оказалось, что периметр каждого из получившихся прямоугольников — целое число метров. Обязательно ли периметр исходного прямоугольника — целое число метров?
Ответ. Да, обязательно.
Решение. Рассмотрим прямоугольники, заштрихованные на рисунке ("диагональные"). Горизонтальная сторона исходного прямоугольника складывается из их горизонтальных сторон. То же — для вертикальной стороны.
Поэтому периметр исходного прямоугольника равен сумме периметров заштрихованных прямоугольников. Периметр каждого из этих прямоугольников — целое число метров. Их сумма – тоже целое число метров.

Задача 5. [8 баллов]
В честь праздника 1% солдат в полку получили новое обмундирование. Солдаты расставлены в виде прямоугольника так, что солдаты в новом обмундировании оказались не менее чем в 30% колонн и не менее чем в 40% шеренг. Какое наименьшее число солдат могло быть в полку?
Ответ. 1200.
Решение. Предположим, что солдаты поставлены в m колонн и n шеренг. Тогда в полку mn солдат, и mn/100 солдат получили новое обмундирование. Согласно условию, не менее чем в 40n/100 шеренг есть хотя бы по одному солдату в новом обмундировании, значит,

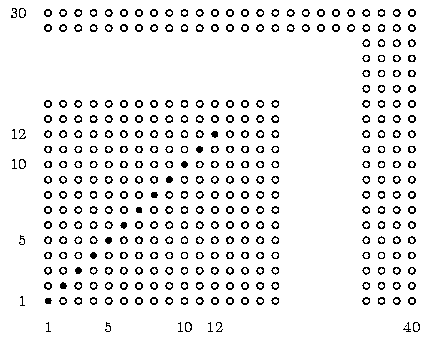
Задача 6. [9 баллов]
Куб размером 3*3*3 состоит из 27 единичных кубиков. Можно ли побывать в каждом кубике по одному разу, двигаясь следующим образом: из кубика можно пройти в любой кубик, имеющий с ним общую грань, причем запрещено ходить два раза подряд в одном направлении?
Ответ. Нельзя.
Решение. Предположим, что можно. В кубе 8 угловых кубиков (на рисунке они покрашены в черный цвет) и 6 "центральных" кубиков (они расположены в центрах граней и заштрихованы на рисунке). Нетрудно видеть, что любой ход из углового кубика ведет в кубик в середине ребра, а следующий ход — в центральный кубик. Таким образом, чтобы попасть из одного углового кубика в другой, придется пройти хотя бы через один центральный. Иными словами, между каждыми двумя соседними (в порядке обхода) угловыми кубиками должен встретиться хотя бы один центральный. Значит, центральных кубиков не меньше семи, а их всего лишь шесть!