16-й Математический Праздник.
13 февраля 2005 года

Условия и решения задач.

7 класс

На выполнение задания школьникам давалось 2 часа (120 минут).

Задача 1. [3 балла] На рисунке изображено, как изменялся курс тугрика в течение недели. У Пети было 30 рублей. В один из дней недели он обменял все свои рубли на тугрики. Потом он обменял все тугрики на рубли. Затем он ещё раз обменял все вырученные рубли на тугрики, и в конце концов, обменял все тугрики обратно на рубли. Напишите, в какие дни он совершал эти операции, если в воскресенье у него оказалось 54 рубля. (Достаточно привести пример.)

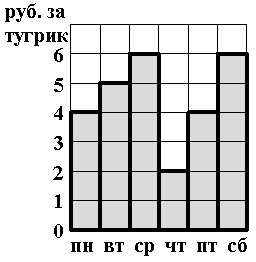
Ответ. Во вторник он обменял свои рубли на 6 тугриков, продал их в среду и получил 36 рублей. В пятницу он обменял полученные рубли на 9 тугриков. Продав их в субботу, он получил 54 рубля.

Задача 2. Можно ли расставить числа
а) [3 балла] от 1 до 7;
б) [3 балла] от 1 до 9
по кругу так, чтобы любое из них делилось на разность своих соседей?

Ответ. а) Да, см. рис.;

Решение. б) Заметим, что нечётное число не делится на чётное, а значит, не может стоять в окружении чисел одинаковой чётности. Отсюда следует, что нечётные числа стоят парами. Однако среди чисел 1, 2, ..., 9 нечётных чисел пять, и поэтому из них нельзя образовать пары.

Задача 3. [4 балла] Зачеркните все шестнадцать точек, изображённых на рисунке, шестью отрезками, не отрывая карандаша от бумаги и не проводя отрезков по линиям сетки.

Ответ. Пример изображён на рисунке.

Примечание. Можно доказать, что этот пример единственен с точностью до поворота на 90^o.

Задача 4. Бумага расчерчена на клеточки со стороной 1. Ваня вырезал из неё по клеточкам прямоугольник и нашёл его площадь и периметр. Таня отобрала у него ножницы и со словами "Смотри, фокус!" вырезала с краю прямоугольника по клеточкам квадратик, квадратик выкинула и объявила: "Теперь у оставшейся фигуры периметр такой же, какая была площадь прямоугольника, а площадь - как был периметр!" Ваня убедился, что Таня права.
а) Квадратик какого размера вырезала и выкинула Таня? [2 балла]
б) Приведите пример такого прямоугольника и такого квадрата. [3 балла]
в) Прямоугольник каких размеров вырезал Ваня? [4 балла]

(А. Хачатурян.)

Ответ. а) 2*2; б) см. рис. к п. в) решения; в) 3*10 или 4*6.

Решение. а) Квадратик не мог иметь общий угол с прямоугольником (см. рис.), так как тогда периметр остался бы прежним или уменьшился (убедитесь сами!), а площадь бы уменьшилась. Значит квадрат примыкает только к одной из сторон прямоугольника (см. рис.).

Пусть сторона квадрата x. Тогда Таня, вырезав квадрат, уменьшила площадь фигуры на x², при этом периметр увеличился на две стороны квадрата, то есть на 2x. Таким образом,

исходная площадь - x² = площадь полученной фигуры,
исходный периметр + 2x = периметр полученной фигуры.

исходная площадь = периметр полученной фигуры,
исходный периметр = площадь полученной фигуры.

исходная площадь - x² = исходный периметр,
исходный периметр + 2x = исходная площадь.

в) Пусть стороны прямоугольника m и n. Тогда из решения пункта а) следует, что mn=2m+2n+4. Наша задача - найти все возможные пары чисел m и n, удовлетворяющие этому равенству. Можно рассуждать так. Ясно, что m и n превосходят 2, иначе квадрат 2*2 вырезать нельзя. Пусть m>n. Тогда, при m>n>5, 2m+2n+4<4m+4<5m<mn. Значит, 2<n<5. Подставляя n=3, находим m=10, а при n=4 получаем m=6. Таким образом, прямоугольники могли быть только такие, как показано на рисунках - 3*10 и 4*6.

Можно рассуждать иначе. Равенство mn=2m+2n+4 можно записать в виде (n-2)(m-2)=8. Поскольку m и n превосходят 2, задача сводится к поиску разложений числа 8 на два натуральных множителя.

Задача 5. Решите ребус 250*ЛЕТ+МГУ=2005*ГОД. (Разными буквами обозначены разные цифры, а одинаковыми - одинаковые; при этом некоторыми буквами могут быть обозначены уже имеющиеся цифры 2, 5 и 0.)
а) [4 балла] Найдите хотя бы одно решение ребуса;
б) [4 балла] Докажите, что других решений нет.

Ответ. 250*984+615=2005*123.

Решение.
 

1) Заметим, что при Л<7 левая часть не превосходит 250*800+1000=201000, а правая не меньше 2005*102=204510. Значит, Л=8 или Л=9.	Л = 8; 9
2) Если ГОД>124, то число в правой части не меньше 2005*124=248620, а в левой части - не больше 250*987+1000=247750. Значит, ГОД<123 и Г=1, а потому О=0 или О=2.	Г=1 О=0; 2
3) Выражение в правой части и число 250 делятся на 5, поэтому либо У=5, либо У=0. Покажем, что второй случай невозможен. В самом деле, если У=0, то правая часть оканчивается нулём и потому чётна, а значит, Д чётно. При этом О=2 (так как О не равно 0), и минимальное значение Д равно 4, то есть ГОД>124. Это противоречит пункту 2). Значит, У=5, откуда следует, что Д нечётно.	У=5 Д=2k+1
4) Для цифры Д есть всего 3 значения: Д=3, Д=7, и Д=9. Рассмотрим остатки от деления на 50 выражений в левой и правой частях. Слева будет остаток 15 (так как Г=1 и У=5), значит, он должен быть таким же справа, что возможно лишь при Д=3.	Д=3
5) Определим значение О. Допустим, что О = 0. Тогда справа получаем 2005*103=206515, а значит, цифра Т чётна (иначе в разряде десятков слева не получится единицы). Тогда ЛЕТ>824, а М>6 (остальные цифры заняты), и правая часть окажется меньше левой. Значит, О=2.	О=2
6) Имеем ГОД=123. Случай Л=8 не годится (слишком мало), остаётся Л=9. По тем же соображениям Е>8, а так как цифра 9 занята, то Е=8. Далее легко видеть, что Т=4 и М=6.	Л=9 Е=8

Примечание. Вполне возможны и иные рассуждения (даже решение прямым подбором), но приведённое решение одновременно решает пункты a) и б).

Задача 6. [8 баллов] На острове Невезения с населением 96 человек правительство решило провести пять реформ. Каждой реформой недовольна ровно половина всех граждан. Гражданин выходит на митинг, если он недоволен более чем половиной всех реформ. Какое максимальное число людей правительство может ожидать на митинге? (Приведите пример и докажите, что больше нельзя.)

Ответ. 80.

Решение. Пусть x - число людей, вышедших на митинг. Рассмотрим общее число "недовольств". С одной стороны, каждой реформой недовольно ровно 48 жителей, а значит, общее число недовольств равно 48*5=240. С другой стороны, каждый вышедший на митинг недоволен хотя бы тремя реформами. Следовательно, общее число недовольств не меньше, чем 3x. Таким образом, 240>3x, откуда x<80. Итак, искомое число не больше 80.
Приведём пример, когда на площадь выйдет ровно 80 человек. Выберем среди жителей острова 80 человек и разобьём их на пять групп по 16 человек. Пусть против первой реформы возражают люди из первых трёх групп, против второй - люди из второй, третьей и четвёртой групп, против третьей - люди из третьей, четвёртой и пятой групп, против четвёртой - люди из четвёртой, пятой и первой групп, а против пятой - люди из пятой, первой и второй групп. Тогда против каждой реформы возражают ровно 3*16=48 человек, и на митинг выйдут выбранные 80 человек.

Дата последнего изменения — 13 февраля 2005 года