17-й Математический Праздник.
12 февраля 2006 года

Условия и решения задач.

7 класс

На выполнение задания школьникам давалось 2 часа (120 минут).

Задача 1. Винни-Пух и Пятачок поделили между собой торт. Пятачок захныкал, что ему досталось мало. Тогда Пух отдал ему треть своей доли. От этого у Пятачка количество торта увеличилось втрое. Какая часть торта была вначале у Пуха и какая у Пятачка? [4 балла]

Ответ. 6/7 и 1/7.

Решение. Треть доли Пуха увеличила втрое порцию Пятачка, то есть сама была вдвое больше неё. Значит, вся доля Пуха была в 6 раз больше доли Пятачка, то есть у Пуха было вначале 6/7 торта, а у Пятачка - 1/7.

Задача 2. Разрежьте изображённый на первом рисунке пятиугольник на две одинаковые (совпадающие при наложении) части. [5 баллов]

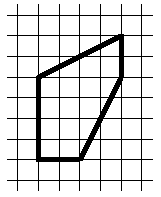
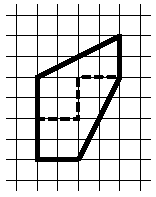
Ответ. Искомый разрез показан на втором рисунке.

Задача 3. Наташа сделала из листа клетчатой бумаги календарь на январь 2006 года (см. рисунок) и заметила, что центры клеток 10, 20 и 30 января образуют равнобедренный прямоугольный треугольник. Наташа предположила, что это будет верно и в любом другом году, за исключением тех лет, когда центры клеток 10, 20 и 30 лежат на одной прямой. Права ли Наташа? [5 баллов]

Ответ. Наташа права.

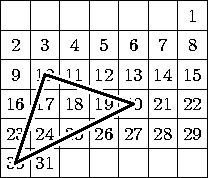
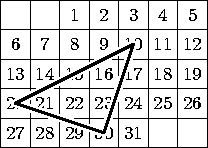
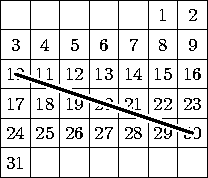
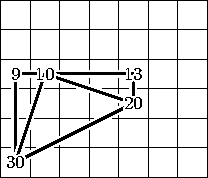
Решение. Всего существует 7 различных вариантов расположения дат в январском календаре. При этом существует всего 2 существенно различных варианта расположения треугольника 10-20-30 (см. первые два рисунка), все остальные получаются из первых двух горизонтальными сдвигами треугольника. Проверим Наташино предположение для первого случая, а для второго случая рассуждения будут аналогичными. Очевидно, что у треугольника 30-9-10 угол 9 прямой (см. четвёртый рисунок), и, аналогично, является прямым угол 13 у треугольника 10-13-20. Ясно, что стороны 9-30 и 10-13 равны; аналогично, равны стороны 9-10 и 13-20. Поэтому треугольники 9-30-10 и 13-10-20 равны по двум сторонам и углу между ними. Значит, отрезки 10-30 и 10-20 равны. Так как сумма углов в треугольнике равна 180^o, получаем, что сумма острых углов в треугольнике 9-10-30 равна 180^o-90^o=90^o. Осталось заметить, что сумма углов, дополняющих угол 10 до развёрнутого угла, равна сумме острых углов треугольника 9-10-30. Значит, угол 10 тоже равен 90^o. Итак, треугольник 10-20-30 является равнобедренным прямоугольным.

Задача 4. Год проведения нынешнего математического праздника де- лится на его номер: 2006 : 17 = 118.
а) Назовите первый номер матпраздника, для которого это тоже было выполнено. [2 балла]
б) Назовите последний номер матпраздника, для которого это тоже будет выполнено. [5 баллов]

Ответ. а) 1;   б) 1989.

Решение. а) Первый матпраздник был в 1990 году. Ясно, что год его проведения делится на его номер, потому что номер равен единице.

б) Пусть N - номер матпраздника. Тогда год его проведения равен (2006-17)+N=1989+N. Пусть год проведения делится на номер, то есть 1989+N делится на N. Значит, 1989 делится на N. Поскольку мы ищем наибольшее возможное N, то нужно взять N=1989.

Задача 5. Дед звал внука к себе в деревню: "Вот посмотришь, какой я необыкновенный сад посадил! У меня там растут груши и яблони, причём яблони посажены так, что на расстоянии 10 метров от каждой яблони растёт ровно две груши". - "Ну и что тут интересного, - ответил внук. - У тебя, значит, яблонь вдвое меньше, чем груш". "Авот и не угадал, - улыбнулся дед. - Яблонь у меня в саду вдвое больше, чем груш". Нарисуйте, как могли расти яблони и груши в саду у деда. [7 баллов]

Ответ. Например, сад может выглядеть так, как показано на первом рисунке.

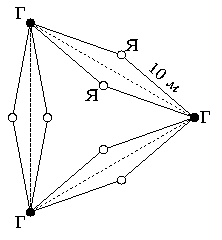
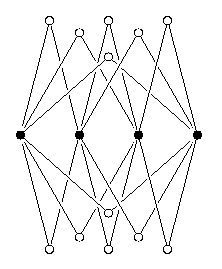
Комментарий. На самом деле, можно так расположить груши и яблони, что яблонь будет во много раз больше, чем груш. Расставим груши на одной прямой через равные расстояния так, чтобы расстояние между первой и последней не превосходило 20 метров. После этого берём любые две груши (назовём их A и B) и ставим яблонюв вершине равнобедренного треугольника с основанием AB и боковыми сторонами длиной 10 метров. Ещё одну яблоню ставим симметрично этой яблоне относительно линии груш (см. второй рисунок). Значит, яблонь можно поставить вдвое больше числа пар груш, а оно равно n(n-1)/2. Мы сможем поставить (n(n-1)2)*2=n(n-1) яблонь. Заметим, что в этом случае отношение числа яблонь и числа груш равно n(n-1)/n=n-1, значит, выбирая достаточно большие n, это отношение можно сделать сколь угодно большим.

Задача 6. Петя закрасил одну клетку прямоугольника. Саша может закрашивать другие клетки этого прямоугольника по следующему правилу: можно красить любую клетку, у которой нечётное число закрашенных соседей (по стороне). Сможет ли Саша закрасить все клетки прямоугольника (независимо от того, какую клетку выбрал Петя), если размеры прямоугольника
а) 8*9 клеток? [4 балла]
б) 8*10 клеток? [7 баллов]

Ответ. а) Да;   б) Нет.

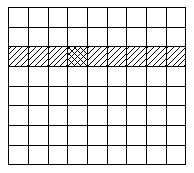
Решение. а) Сначала закрасим ряд длиной 9 клеток, содержащий изначально закрашенную клетку (см. первый рисунок). Далее будем красить столбцы через один, начиная закраску от покрашенного ряда (см. второй рисунок). После этого закрасить оставшиеся клетки доски совсем просто.

Комментарий. Данный способ покраски обобщается на тот случай, когда хотя бы одна из сторон прямоугольника имеет нечётную длину. Повернём прямоугольник так, чтобы его ширина была нечётной, а после этого повторим только что описанную процедуру: красим ряд нечётной длины, и так далее.

б) Первый способ. Посмотрим на полупериметр фигуры, состоящей из закрашенных клеток. Вначале, когда закрасили одну клетку, полупериметр равен 2. На каждом шаге полупериметр или увеличивается на 1 (если у клетки была только одна соседняя закрашенная клетка) или уменьшается на 1 (если таких соседей было 3), то есть полупериметр увеличивается или уменьшается на 1. Следовательно, когда закрашено чётное число клеток, полупериметр закрашенной фигуры нечётен. Заметим, что полупериметр всего прямоугольника 8*10 равен 18, то есть чётный, поэтому весь прямоугольник закрасить нельзя.

Второй способ. Докажем, что для чётных m и n прямоугольник m*n нельзя закрасить ни при какой начальной закрашенной клетке. Посмотрим, сколько всего сторон имеют клеточки (включая внешние). Сторон клеточек m(n+1)+n(m+1)=2mn+m+n, то есть чётное число. Предположим, что мы смогли закрасить весь прямоугольник. Будем называть сторону закрашенной, если закрашена хотя бы одна из прилегающих к ней клеток. Вначале закрашено 4 стороны. На каждом шаге закрашивается 1 или 3 стороны. Всего таких шагов нужно сделать nm-1. Поскольку m и n чётны, то число nm-1 нечётно. Итак, если бы мы смогли закрасить весь прямоугольник, то было бы закрашено 4+(нечётное число раз по нечётному числу) сторон, то есть нечётное число, но, как мы уже посчитали, таких сторон чётное число, значит, весь прямоугольник закрасить нельзя.

Дата последнего изменения — 12 февраля 2006 года