18-й Математический Праздник.
11 февраля 2007 года

Условия и решения задач.

7 класс

На выполнение задания школьникам давалось 2 часа (120 минут).

Задача 1. Даша и Таня живут в одном подъезде. Даша живёт на 6 этаже. Выходя от Даши, Таня пошла не вниз, как ей было нужно, а вверх. Дойдя до последнего этажа, Таня поняла свою ошибку и по- шла вниз на свой этаж. Оказалось, что Таня прошла в полтора раза больше, чем если бы она сразу пошла вниз. Сколько этажей в доме? [4 балла]

Ответ. 7 этажей.

Решение. Пусть с шестого этажа Тане надо было спуститься на n этажей. Тогда Таня прошла "лишний путь" вверх до последнего этажа и обратно до шестого. Длина лишнего пути 1,5n-n=0,5n этажей. Половину этого лишнего пути Таня шла вверх, а половину - вниз. Значит, вверх она поднялась на n/4 этажей. Если она поднялась на один этаж (n/4=1), то Таня живет на 4 этажа ниже Даши и в доме 7 этажей. Если же n/4 равно 2 или больше, то Тане пришлось бы спуститься с шестого этажа минимум на 8 этажей вниз, что невозможно.

Задача 2. В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторыми из них знак умножения. Произведение получившихся чисел оказалось равным 2007. Какая отметка выходит у Вовочки в четверти по пению? ("Колов" учительница пения не ставит.) [4 балла]

Ответ. Тройка.

Решение. Разложим число 2007 на простые множители:

2007=3*3*223.

Отсюда можно было бы сделать вывод, что отметки Вовочки - это две двойки и три тройки. Но на самом деле надо ещё доказать, что нет других вариантов отметок. Посмотрим, как ещё можно разложить 2007 на множители: 2007=9*223=3*669. Поскольку отметки 9 не бывает, эти разложения числа 2007 не могли возникнуть из Вовочкиных отметок. Так как троек у Вовочки больше, чем двоек, и последняя отметка, как ни переставляй множители, - тройка, можно надеяться, что тройку в четверти он получит.

Задача 3. У Алёны есть мобильный телефон, заряда аккумулятора которого хватает на 6 часов разговора или 210 часов ожидания. Когда Алёна садилась в поезд, телефон был полностью заряжен, а когда она выходила из поезда, телефон разрядился. Сколько времени она ехала на поезде, если известно, что Алёна говорила по телефону ровно половину времени поездки? [6 баллов]

Ответ. 11 часов 40 минут.

Первое решение. Во время разговора энергия аккумулятора расходуется в 210/6=35 раз быстрее, чем в то время, когда разговор не ведётся. Пусть Алёна проговорила x часов. Тогда энергии аккумулято- ра осталось на (6-x) часов разговора или на 35*(6-x) часов ожидания. По условию это время также равно x часов ожидания, поэтому 35*(6-x)=x, откуда x=35*6/36=35/6 часов, то есть 5 ч 50 мин. И, значит, вся поездка продолжалась 11 ч 40 мин.

Второе решение. Если бы Алёна говорила 210*6 часов и молчала 210*6 часов, то телефон бы полностью разрядился 210+6=216 раз. Так как на на самом деле телефон разрядился один раз, Алёна говорила 210*6/216 часов и молчала 210*6/216 часов, то есть ехала она 2*(210*6/216) часов. После сокращения получаем 11 часов 40 минут.

Примечание. Ответ в этой задаче является средним гармоническим чисел 6 и 210 (средним гармоническим чисел a и b называется число 2/((1/a)+(1/b))=2ab/(a+b)).

Задача 4. На клетчатой бумаге отмечены четыре узла сетки, образующие квадрат 4*4. Отметьте ещё два узла и соедините их замкнутой ломаной так, чтобы получился шестиугольник (не обязательно выпуклый) площади 6 клеток. [6 баллов]

Ответ.

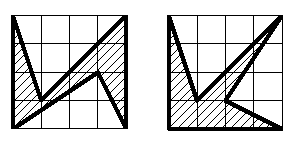
Решение. Можно попытаться найти решение, просто пробуя различные пары вершин внутри квадрата 4*4 и стараясь сделать получаемый шестиугольник поуже. При этом удобнее считать не площадь шестиугольника, а площадь оставшейся части квадрата - она должна быть равна 10 клеткам.

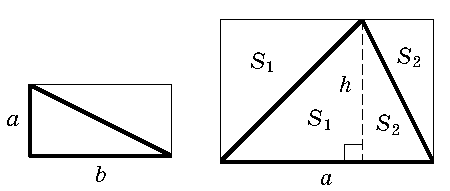
Для подсчёта площади можно разбить оставшуюся часть на прямоугольные треугольники и вспомнить, что площадь прямоугольного треугольника, катеты которого идут по линиям сетки, равна половине площади прямоугольника со сторонами a и b (см. рис. слева) и равна ab/2 (эта формула верна и для произвольного прямоугольного треугольника). Те из вас, кто знает более общую формулу: площадь треугольника со стороной a и опущенной на неё высотой h равна ah/2 (см. рис. справа), могут сразу найти площадь произвольного треугольника, не разбивая его на прямоугольные.

Задача 5. Нарисуйте, как из данных трёх фигурок, использовав каждую ровно один раз, сложить фигуру, имеющую ось симметрии. [7 баллов]

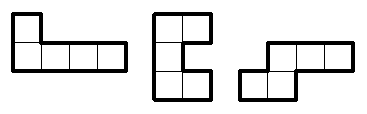
Решение. Из предложенных фигурок можно сложить четыре различные фигуры, имеющие ось симметрии. Две из них приведены на рисунке. У одной из них ось симметрии вертикальная, а у другой проходит по диагонали. Это не случайно - ось симметрии фигуры, нарисованной по клеточкам, может быть либо параллельна сторонам клеток, либо идти под углом 45 градусов к ним.

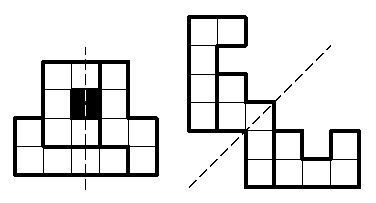
Попробуйте найти остальные два решения.

Задача 6. Буратино ходит по улицам города, на одном из перекрёстков которого зарыт клад. На каждом перекрёстке ему по радио сообщают, приблизился он к кладу или удалился (по сравнению с предыдущим перекрёстком). Радио либо всегда говорит правду, либо всегда лжёт (но Буратино не знает, лжёт оно или нет).

Сможет ли Буратино точно узнать, где закопан клад, если план города имеет вид:
а) [4 балла],

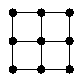
б) [5 баллов]?

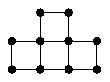
(Перекрёстки отмечены точками.)

Ответ. а) Нет, не всегда; б) да, всегда сможет найти.

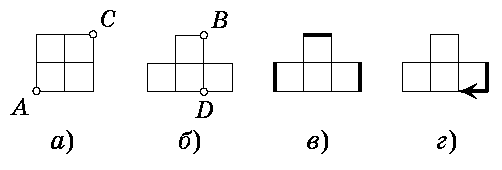
Решение. а) Всегда, когда Буратино приближается к перекрёстку A, он удаляется от перекрестка C (см. рис. а). Поэтому, Буратино не сможет различить следующие две ситуации:
1) Клад закопан на перекрестке A и радио говорит правду;
2) Клад закопан на перекрестке C и радио лжет.

б) Заметим, что если Буратино знает, что радио говорит правду, то он сможет найти клад. Действительно, двигаясь по улице BD сверху вниз (см. рис. б), он найдёт горизонтальную улицу, на которой лежит клад. Затем, двигаясь по этой горизонтальной улице слева направо, он найдёт точное местоположение клада. Если же Буратино знает, что радио лжёт, то он всё равно сможет найти клад (действуя тем же способом, но заменяя указания радио на противоположные).

Теперь Буратино остается выяснить, лжёт ли радио.

Пусть вначале Буратино предположит, что радио говорит правду, и попытается найти клад. Действуя, как описано выше, он найдёт точку T, в которой может быть зарыт клад, либо (если сообщения радио будут противоречивы) поймёт, что радио лжет.

Аналогично, предположив, что радио лжёт, Буратино найдёт точку L, в которой предположительно лежит клад, либо сможет установить, что радио говорит правду.

Итак, проделав это, Буратино либо уже установил, говорит ли радио правду, либо нашёл две точки T и L, в одной из которых точно находится клад.

Рассмотрим на плане города три отрезка (см. рис. в). Хотя бы на одном из них не лежит ни T, ни L. Поэтому Буратино может встать в один из концов этого отрезка и совершить переход в соседнюю точку, не лежащую на этом отрезке (рис. г). При этом он приблизится как к T, так и к L.

Таким образом Буратино определит, лжет ли радио, и узнает, где находится клад.

Опубликовано 11 февраля 2007 года