1. Шеренга новобранцев стояла лицом к сержанту. По команде
"налево" некоторые повернулись налево, некоторые - направо, а остальные -
кругом. Всегда ли сержант сможет встать в строй так, чтобы с обеих сторон
от него оказалось поровну новобранцев, стоящих к нему лицом?
(фольклор, формулировка - А. Шаповалов)
Ответ: всегда.
Решение. Договоримся в случае, когда сержант стоит в строю, обозначать буквой m количество человек, стоящих в строю слева от сержанта к нему лицом, а буквой n - количество человек, стоящих справа от сержанта к нему лицом.
Пусть сначала сержант встанет в левый край шеренги. Тогда слева от него никого не будет (m=0). Если и справа от сержанта никто не будет стоять к нему лицом (n=0), то задача решена. В противном случае (n>0) пусть сержант идёт слева направо от человека к человеку. Если он проходит новобранца, стоявшего к нему спиной, то число m увеличивается на 1, а число n не изменяется. Если сержант проходит новобранца, стоявшего к нему лицом, то число n уменьшается на 1, а число m не изменяется. Иначе оба числа m и n остаются без изменений. Тем самым, число m-n сначала отрицательно, а в процессе движения сержанта вдоль строя может увеличиваться не более чем на 1 при прохождении каждого новобранца. Но когда сержант дойдёт до правого края, уже число n будет нулевым, а значит, число m-n будет неотрицательным. Итак, начав с отрицательного числа m-n и прибавляя к нему несколько раз по единице, мы получили неотрицательное число. Значит, в какой-то момент мы должны были получить ноль, то есть в тот момент m=n и с обеих сторон от сержанта лицом к нему находилось поровну новобранцев.
2. Пусть a, b, c - стороны треугольника,
Докажите неравенство
a3+b3+3abc>c3
(В. Сендеров)
Решение. Используя неравенство треугольника a+b>c и то, что a2-ab+b2>0, получаем цепочку неравенств:
a3+b3+3abc=(a+b)(a2-ab+b2)+3abc>
>c(a2-ab+b2)+3abc=c(a2+2ab+b2)=c(a+b)2>c*c2=c3.
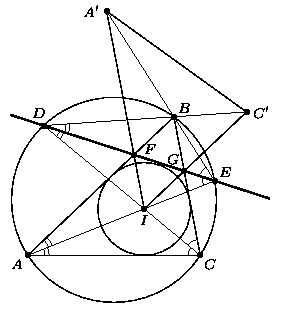
3. Биссектрисы углов A и С треугольника ABC
пересекают описанную около него окружность в точках E и D
соответственно. Отрезок DE пересекает стороны AB и BC
соответственно в точках F и G. Пусть I - точка
пересечения биссектрис треугольника ABC. Докажите, что
четырёхугольник BFIG - ромб.
(В. Жгун)
Решение. Отразим треугольник ABC относительно прямой DE (см. рис.). По свойству вписанных углов /AED=/ACD=/BCD=/BED, поэтому прямая AE при этом отражении перейдёт в прямую BE, аналогично, прямая CD при отражении перейдёт в прямую BD. Тогда точка пересечения прямых AE и CD, то есть точка I, перейдёт при отражении в точку пересечения прямых BE и BD, то есть в точку B. Таким образом, треугольник IFG перейдёт при нашем отражении в треугольник BFG, откуда IF=BF, IG=BG и прямая BI перпендикулярна DE. Но луч BI - биссектриса угла FBG, и поэтому треугольник FBG - равнобедренный, то есть FB=BG.
Итак, все стороны четырёхугольника BFIG равны, значит, это ромб.

4. Найдите все целые числа x и y, удовлетворяющие
уравнению
x4-2y2=1.
(В. Сендеров)
Ответ: x=1, y=0 или x=-1, y=0.
Решение. Знаки x и y можно выбирать произвольно, поэтому будем искать только неотрицательные решения. Ясно, что x - нечётное число, x=2t+1.П ерепишем уравнение в виде
x4-1=(x-1)(x+1)(x2+1)=2t*(2t+2)*(4t2+4t+2)=2y2.
Теперь видно, что y - чётное число, y=2u. Получаем уравнение нан еотрицательные t, u:
t(t+1)(2t(t+1)+1)=u2.
Числа t, t+1 и 2t(t+1)+1 попарно взаимно просты, а ихп роизведение - полный квадрат. Значит, каждое из них также является полным квадратом. Это возможно только при t=0 (единственная пара последовательных полных квадратов - это 0 и 1). Тогда и u=0.З начит, x=+1, y=0.
5. В ряд расположили n лампочек и зажгли некоторые из них.
Каждую минуту после этого все лампочки одновременно меняют состояние
по следующему правилу. Те лампочки, которые горели на прошлой минуте,
гаснут. Те, которые на прошлой минуте не горели и соседствовали ровно
с одной горящей лампочкой, загораются. При каких n можно так
зажечь некоторые лампочки в начале, чтобы потом в любой момент нашлась
хотя бы одна горящая лампочка?
(А. Горбачёв)
Ответ: при всех n, кроме 1 и 3.
Решение. См. решение задачи 8.6, где данной задаче соответствует случай прямоугольников 1*n (горящие лампочки - это живые клетки).
6. Остроугольный треугольник разрезали прямолинейным разрезом
на две (не обязательно треугольные) части, затем одну из этих частей -
опять на две части, и так далее: на каждом шаге выбирали любую из уже
имеющихся частей и разрезали её (по прямой) на две. Через несколько шагов
оказалось, что исходный треугольник распался на несколько треугольников.
Могут ли все они быть тупоугольными?
(Г. Гальперин)
Ответ: не могут.
Решение. Докажем индукцией по количеству имеющихся частей следующее утверждение: после каждого разрезания найдётся часть (многоугольник) хотя бы с тремя не тупыми углами.
База индукции. Сначала есть одна часть, и это треугольник с тремя острыми углами.
Шаг индукции. Пусть на очередном шаге имеется многоугольник M хотя бы с тремя не тупыми углами и мы делаем очередное разрезание.
Если мы режем не многоугольник M, то шаг индукции доказан. Пусть мы разрезали M по прямой на две части. Обозначим точки пересечения этой прямой с многоугольником M буквами A и B.
Если точка A лежит внутри одной из сторон многоугольника M, то линия разреза образует с этой стороной два смежных угла, по крайней мере один из которых - не тупой. Если же точка A - вершина многоугольника, то соответствующий ей угол многоугольника разбивается разрезом на два угла, сумма которых меньше 180o. Значит, тем более один из них не тупой. Если при этом угол A сам не был тупым, то, очевидно, оба получившихся угла также не тупые. Таким образом, после разреза к точке A примыкает больше не тупых углов (по крайней мере на единицу). Аналогичные рассуждения про второй конец разреза показывают, что дополнительный не тупой угол появляется и там.
По предположению индукции многоугольник M имел не менее трёх не тупых углов. Поэтому после разрезания у двух получившихся многоугольников таких углов в сумме не менее пяти. Но согласно принципу Дирихле по крайней мере в одном из них не тупых углов не менее трёх. Шаг индукции доказан.
Тем самым, утверждение доказано. Значит, после того как исходный треугольник распадётся на треугольники, хотя бы у одного из них будет не меньше трёх не тупых углов, то есть все углы этого треугольника будут не тупыми.