 .
.Задания | Результаты | Решения (doc-файл)
Первый тур (10 минут; каждая задача - 6 баллов
1.1. Решите неравенство: 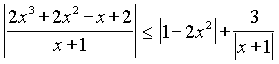 .
.
1.2. В треугольнике АВС биссектрисы AD и СE пересекаются в точке О; Ð АВС = 60° . Докажите, что OD = OE.
1.3. Пусть f(x) - некоторая функция, определенная на всей числовой прямой. Известно, что функция f(f(x)) - возрастающая. Верно ли, что функция f(x) - монотонная?
Второй тур (15 минут; каждая задача - 7 баллов
).2.1.
Найдите все целые решения уравнения2.2.
В треугольной пирамиде АВСD ребра АВ и CD имеют длины а и b соответственно. Найдите сумму квадратов длин двух отрезков, один из которых соединяет середины АС и BD, а другой - середины ВС и AD.2.3. Саша вычислил значение 2002!. В числе, полученном Сашей, Андрей слева направо поставил знаки действий: между первой и второй цифрами знак ╓-╞, между второй и третьей цифрами знак ╓+╞, между третьей и четвертой - ╓-╞, и так далее, до конца. Затем, Саша вычислил результат этих действий. В полученном Сашей числе Андрей опять поставил между цифрами знаки ╓-╞ и ╓+╞ по такому же правилу. Саша опять вычислил результат, и так далее. После некоторого количества таких операций было получено однозначное число. Какое?
Третий тур (15 минут; каждая задача - 7 баллов
).3.1.
Для действительных чисел x, y и z выполняются два условия: x + y + z = 5 и xy + yz + zx = 8. Докажите, что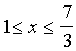 .
.
3.2.
Десять точек A1, A2, ..., A10 делят окружность единичного радиуса на 10 равных дуг. Найдите разность: A1A4 - A1A2.3.3. На окружности единичного радиуса произвольным образом отмечено 100 точек. Верно ли, что на этой окружности обязательно найдется еще одна точка, сумма расстояний от которой до всех отмеченных, не меньше ста?
Четвертый тур (20 минут; каждая задача - 8 баллов
).4.1.
Решите уравнение: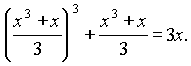
4.2.
Диагональ ВD вписанного четырехугольника АВСD является биссектрисой угла AВC. Найдите площадь этого четырехугольника, если BD = 6 см, Ð АВС = 60° .4.3.
Из бесконечной последовательности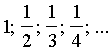 выберите 6 чисел, которые составляют арифметическую прогрессию.
выберите 6 чисел, которые составляют арифметическую прогрессию.
Пятый тур (25 минут; каждая задача - 9 баллов
).5.1.
Решите уравнение: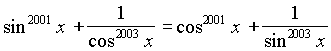 .
.
5.2.
В основании пирамиды, имеющей объем V, лежит параллелограмм. Длины боковых ребер этой пирамиды различны и отличны от длин ребер основания. Найдите объем треугольной пирамиды, составленной из боковых граней данной пирамиды.5.3.
Найдите наибольшее и наименьшее значения выражения| 1 тур | 2 тур | 3 тур | 4 тур | 5 тур | Сумма | |||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||
| 7 А | 0 | 0 | 0 | 7 | 7 | 0 | 0 | 3 | 0 | 8 | 5 | 0 | 1 | 0 | 1 | 32 |
| 7 Б | 5 | 0 | 0 | 5 | 7 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 1 | 0 | 0 | 22 |
| 91А | 6 | 0 | 6 | 7 | 5 | 0 | 7 | 0 | 0 | 8 | 0 | 8 | 1 | 9 | 1 | 58 |
| 91Б | 0 | 6 | 0 | 7 | 7 | 6 | 1 | 3 | 0 | 8 | 8 | 0 | 1 | 0 | 9 | 56 |
| 109А | 6 | 2 | 0 | 7 | 7 | 7 | 0 | 3 | 0 | 8 | 3 | 0 | 3 | 1 | 9 | 56 |
| 109Б | 6 | 2 | 0 | 1 | 7 | 1 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 22 |
| 152 | 0 | 0 | 0 | 2 | 7 | 1 | 7 | -1 | 0 | 1 | 0 | 8 | 1 | 0 | 1 | 27 |
| 174 | 0 | 0 | 0 | 2 | 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 12 |
| 199 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 1 | 10 |
| 654 | 1 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 14 | |
| 1018 | 5 | 0 | 0 | 7 | 7 | 0 | 0 | 3 | 0 | 1 | 0 | 7 | 1 | 0 | 1 | 32 |
| 1101А | 6 | 0 | 0 | 1 | 3 | 2 | 1 | 0 | 0 | 8 | 7 | 8 | 6 | 0 | 9 | 51 |
| 1101Б | 6 | 0 | 0 | 7 | 7 | 0 | 0 | 0 | 8 | 0 | 0 | 1 | 0 | 9 | 38 | |
| 1101В | 5 | 0 | 0 | 7 | 3 | 7 | 7 | 7 | 0 | 8 | 0 | 8 | 1 | 0 | 0 | 53 |
| 1101Г | 1 | 2 | 0 | 7 | 3 | 1 | 0 | 2 | 0 | 1 | 0 | 8 | 1 | 1 | 0 | 27 |
| 1511А | 0 | 0 | 0 | 7 | 0 | 7 | 5 | 0 | 8 | 0 | 0 | 1 | 0 | 1 | 29 | |
| 1511Б | 6 | 0 | 0 | 6 | 3 | 0 | 0 | 0 | 0 | 8 | 8 | 4 | 0 | 1 | 36 | |
| 1511В | 6 | 2 | 0 | 7 | 7 | 1 | 1 | 5 | 0 | 8 | 0 | 0 | 1 | 0 | 0 | 38 |
| 1514А | 6 | 5 | 6 | 7 | 7 | 7 | 0 | 3 | 0 | 8 | 0 | 8 | 6 | 1 | 9 | 73 |
| МЦФЭО | 1 | 0 | 0 | 7 | 1 | 1 | 0 | 3 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 16 |
| 1543А | 6 | 0 | 7 | 7 | 0 | 3 | 6 | 0 | 0 | 8 | 1 | 0 | 1 | 39 | ||
| 1543Б | 0 | 6 | 0 | 7 | 7 | 0 | 2 | 0 | 0 | 0 | 8 | 6 | 0 | 1 | 37 | |
| 1543В | 0 | 5 | 0 | 7 | 4 | 7 | 0 | 0 | 0 | 8 | 0 | 0 | 6 | 9 | 0 | 46 |
| 1543Г | 6 | 0 | 0 | 7 | 0 | 7 | 0 | 3 | 0 | 8 | 0 | 0 | 1 | 0 | 0 | 32 |
| Дмитров А | 6 | 6 | 0 | 1 | 7 | 7 | 0 | 3 | 0 | 1 | 1 | 5 | 37 | |||
| Дмитров Б | 0 | 0 | 0 | 7 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 11 |
| ЗФТШ 1 | 0 | 1 | 0 | 1 | 3 | 0 | 0 | 1 | 0 | 8 | 1 | 0 | 1 | 16 | ||
| ЗФТШ 2 | 5 | 0 | 0 | 7 | 3 | 0 | 2 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 19 | |
| ЗФТШ 3 | 0 | 6 | 0 | 7 | 7 | 7 | 1 | 7 | 0 | 3 | 0 | 0 | 1 | 0 | 5 | 44 |
| 109В | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 11 |
| 2А | 6 | 3 | 0 | 7 | 5 | 7 | 7 | 0 | 0 | 8 | 8 | 8 | 1 | 9 | 9 | 78 |
| 2В | 5 | 0 | 0 | 7 | 5 | 0 | 7 | 2 | 7 | 3 | 0 | 0 | 7 | 0 | 1 | 44 |