10 класс.
1.1.
Известно, что числа а + b + c иОтвет
: да, верно.Так как
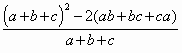 =
= 1.2.
Есть четыре одинаковых кирпича размером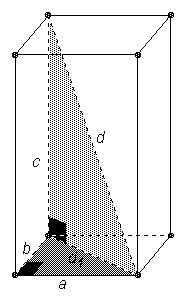
Ответ: см. рис. 1а.

В прямоугольном параллелепипеде, имеющем измерения а
, b и с, d2 = a2 + b2 + c2, где d – длина его диагонали (см. рис. 1б).Существуют два принципиально различных способа сборки параллелепипеда из кирпичей
размером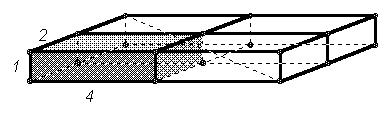
Первый способ
: кирпичи укладываются последовательно в один ряд, например, см. рис. 1б. При такой укладке измерения параллелепипеда будут равны 4а, b и с. Тогда d2 = 16a2 + b2 + c2 = (a2 + b2 + c2) + 15a2, поэтому выгоднее всего увеличивать наибольшее измерение параллелепипеда, то есть прикладывать данные кирпичи друг к другу гранямиДругой способ
: укладка кирпичей в два ряда (см. рис. 1в). При этом d2 = 4a2 + 4b2 + c2 = (a2 + b2 + c2) + 3a2 + 3b2 < (a2 + b2 + c2) + 15a2, если а > b, поэтому такая укладка менее выгодна.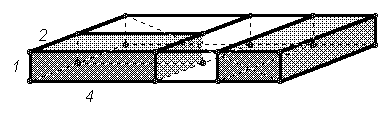
Для данных размеров кирпича возможно изменение предыдущей конструкции, сохраняющее результат сборки (см. рис. 1г), поэтому и в этом случае диагональ параллелепипеда не будет наибольшей из возможных
.1.3.
Найдите все натуральные значения n, при которых n5 + 2 делится на n + 2.Ответ
: 1; 3; 4; 8; 13; 28.Так как
n5 + 2 = (n5 + 25) – 30 и n5 + 25 делится на n + 2, то данное число делится на n + 2 тогда и только тогда, когда n + 2 является делителем числа 30. Учитывая, что n – натуральное, получим: n = 1 или n = 3 или n = 4 или n = 8 или n = 13 или n = 28.Для доказательства того, что
n + 2 является делителем числа 30, можно также применить теорему Безу или деление многочленов (по схеме Горнера или «в столбик») или алгоритм Евклида.
2.1.
Решите уравнение:Ответ
: 0.Так как
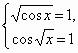 . Из первого уравнения системы получим, что x = 2p
k, где kÎ
Z, а из второго уравнения получим, что
. Из первого уравнения системы получим, что x = 2p
k, где kÎ
Z, а из второго уравнения получим, что 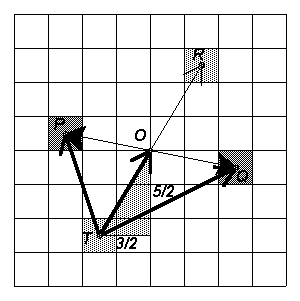
2.2. На шахматной доске построены векторы с началом в центре клетки С2 (см. рисунок) и концами в центрах всех остальных клеток. Найдите модуль суммы этих векторов, если сторона клетки доски равна 1.
Ответ: ![]() .
.
Первый способ
. Пусть Т – общее начало векторов, О – центр квадрата, образующего шахматную доску, а R – точка, симметричная Т относительно О (см. рис. 2а).Для любой пары центров клеток, симметричных относительно точки О выполняется равенство:
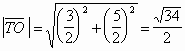 .
.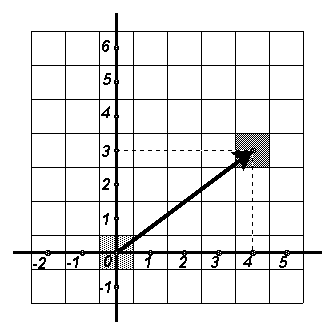
Второй способ
. Введем прямоугольную систему координат с началом в центре клетки С2 (см. рис. 2б).В такой системе координат центр каждой клетки имеет целочисленные координаты вида (i; j) | –2 £
i £
5; –1 £
j £
6. Пусть сумма ![]() указанных векторов имеет координаты (а; b). Так как абсциссу и ординату суммы можно вычислять независимо друг от друга, то
указанных векторов имеет координаты (а; b). Так как абсциссу и ординату суммы можно вычислять независимо друг от друга, то ![]() = 8×
12 = 96;
= 8×
12 = 96; ![]() = 8×
20 = 160.
= 8×
20 = 160.
Тогда
2.3.
Незнайка отметил на плоскости 15 точек и утверждает, что какое бы натуральное число N, где 1 £ N £ 7, ему ни назвали, он сможет указать прямую, содержащую ровно N отмеченных точек. Прав ли он?Ответ
: нет, не прав.Предположим, что Незнайка смог отметить на плоскости 15 точек с таким условием. Рассмотрим три прямые, на одной из которых лежат 7 точек, на другой – 6 точек, а на третьей – 5 точек. Эти прямые различны и имеют не более трех общих точек, поэтому они содержат не менее чем (7 + 6 + 5) – 3 = 15 отмеченных точек, то есть, все точки, отмеченные Незнайкой. Любая прямая, отличная от уже рассмотренных, не может иметь более одной общей точки с каждой из них, то есть, содержит не более трех отмеченных точек. Следовательно, прямой, содержащей ровно 4 отмеченные точки, не существует.
3.1.
Последовательность чисел: 3; 7; 14; 24; ... такова, что разности соседних членов образуют арифметическую прогрессию. Найдите сотый член данной последовательности.Ответ
: 14952.Заметим, что последовательность
(xn), в которой разности соседних членов образуют арифметическую прогрессию, можно записать в виде: x; x + a; x + 2a + d; x + 3a + 3d; ...; x + (n – 1)a + (1 + 2 + ... + (n – 2))d, где а и d – первый член и разность этой прогрессии соответственно. Тогда xn = x + (n – 1)a + (1 + 2 + ... + (n – 2))d = x + (n – 1)a +В нашем случае:
3.2.
Диагонали трапеции АВСD (AD || BC) пересекаются в точке О. Докажите, что окружности, описанные около треугольников АОD и ВОС, касаются друг друга.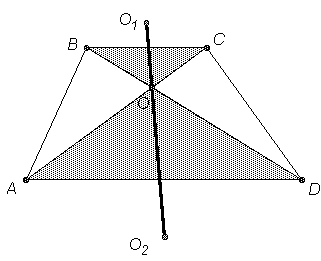
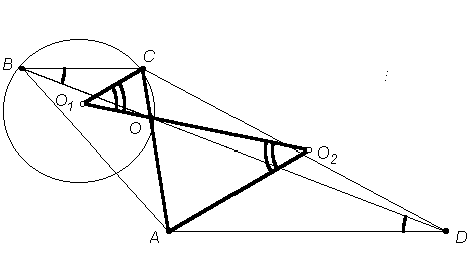
Первый способ. Рассмотрим гомотетию с центром в точке О и коэффициентом
k =Следовательно, точки О
1, О и О2 лежат на одной прямой, то есть, окружности, описанные около треугольников АОD и ВОС, касаются друг друга.Второй способ. Рассмотрим окружность, описанную около треугольника ВОС, и заметим, что хотя бы один из углов ВСА или
CBD является острым, так как они лежат в одном треугольнике ВОС. Пусть, например, острым является Ð CBD = j = Ð ADB (см. рис. 3б). Тогда Ð CO1O = 2j , как центральный угол, опирающийся на ту же дугу. Так как треугольник CO1O – равнобедренный, то Ð CОO1 =Так как точки С, О и А лежат на одной прямой, то полученное равенство углов означает, что и точки О
1, О и О2 также лежат на одной прямой, то есть, окружности, описанные около треугольников АОD и ВОС, касаются друг друга.3.3.
У Васи есть набор из 24 карандашей различных цветов. Он хочет раскрасить некоторое количество кругов по следующему правилу: каждый круг красится в три различных цвета, любое сочетание из двух цветов используется ровно один раз (то есть, если в каком-то круге встретились, например, красный и синий цвета, то ни в каком другом круге такое сочетание цветов невозможно) и каждое сочетание двух цветов должно быть использовано. Сможет ли он это сделать?Ответ: нет, не сможет.
Предположим, что Вася смог раскрасить круги требуемым образом. Выберем один из использованных цветов и рассмотрим все круги в которых он присутствует. В каждом из этих кругов использовано еще по два цвета, причем все эти цвета – различны. Следовательно, их количество – четно. Это противоречит тому, что Васе требуется использовать еще 23 цвета.
4.1.
Решите уравнение:Ответ
:Заметим, что если
x – корень данного уравнения, то |x| £ 1. ПустьУсловию
Отметим, что возведение в квадрат данного уравнения приводит к уравнению 16
y3 – 24y2 + 10y – 1 = 0, где y = x2, не имеющему рациональных корней.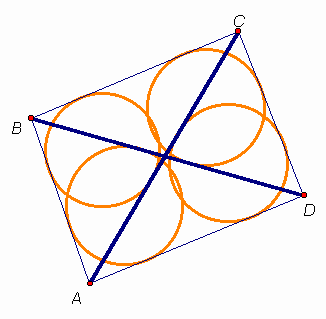
4.2.
Дан выпуклый четырехугольник ABCD. Известно, что равны радиусы окружностей, вписанных в треугольники ABC, ABD, ACD и BCD. Докажите, что АС = BD.Пусть
r – радиус окружностей, перечисленных в условии (см. рис. 4). Так как S =Приравнивая полученные выражения и упрощая равенство, получим, что
|АС| = |BD|, что и требовалось доказать.4.3.
Каждое из первых 2004 простых чисел возвели в степень, равную этому числу. Затем перемножили полученные числа и прибавили единицу. Является ли полученное число точным квадратом?Ответ
: нет, не является.Заметим, что любое простое число, кроме числа 2, является нечетным. Нечетное число в любой натуральной степени – также нечетно, поэтому и их произведение является нечетным числом. Следовательно, полученное число можно записать в виде: 2
2× (2k + 1) + 1 = 8k + 5, где k – некоторое натуральное число. Дальнейшие рассуждения можно провести различными способами.Первый способ. Последовательно возводя в квадрат числа вида: 8
n, 8n ± 1, 8n ± 2, 8n ± 3 и 8n + 4, получим, что полный квадрат при делении на 8 может давать только остатки 0, 1 или 4. Таким образом, полученное число не является точным квадратом.Второй способ. Пусть 2
2× (2k + 1) + 1 = n2, где n – натуральное число. Тогда 4(2k + 1) = (n – 1)(n + 1). Число, стоящее в левой части этого равенства, делится на 4, но не делится на 8. Множители, стоящие в правой части равенства, имеют одинаковую четность и отличаются на 2. Так как число в левой части – четное, то оба этих множителя – четные, причем один из них (и только один) делится на 4. Следовательно, число в правой части равенства должно делиться на 8. Полученное противоречие показывает, что число, указанное в условии, не является точным квадратом.
5.1.
Известно, что x, y и z – положительные числа, произведение которых равно 0,5. Докажите, чтоТак как
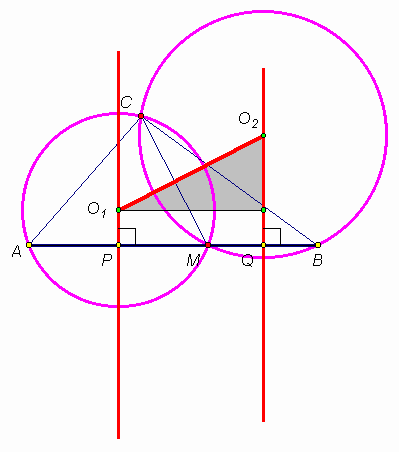
5.2.
М – внутренняя точка отрезка АВ, длина которого 11 см. Рассматриваются всевозможные треугольники АВС. Найдите наименьшее возможное расстояние между центрами окружностей, описанных около треугольников САМ и СВМ.Ответ
: 5,5 см.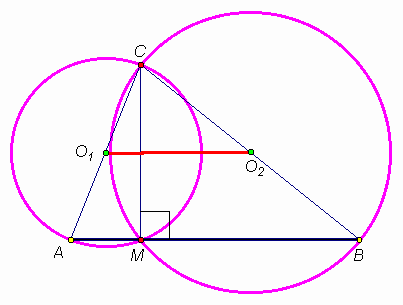
Рассмотрим треугольник АВС, выбрав вершину С произвольно. Точку М на отрезке АВ также выберем произвольным образом (см. рис. 5а). Затем опустим из центров О
1 и О2 данных окружностей перпендикуляры к прямой АВ, обозначив их основания P и Q соответственно. Так центры описанных окружностей лежат на серединных перпендикулярах к сторонам треугольников, то |AP| = |PM|; |MQ| = |QB|, то есть, вне зависимости от положения точки М |PQ| = 0,5|AB| = 5,5 (см). Кроме того, |O1O2| ³ |PQ| (иначе катет соответствующего прямоугольного треугольника оказался бы меньше гипотенузы).Равенство достигается, если СМ
^ АВ (см. рис. 5б). В этом случае, точки O1 и O2 являются серединами гипотенуз прямоугольных треугольников СМА и СМВ, а отрезок O1O2 будет средней линией треугольника АВС, то есть, |O1O2| = 0,5|AB| = 5,5 (см).
5.3.
На шахматной доске стоят десять белых фигур. Докажите, что можно поставить на эту доску черного коня так, чтобы он не нападал ни на одну из этих фигур.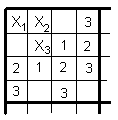
Мысленно разобьем шахматную доску на четыре квадрата размером 4´ 4. Так как белых фигур – 10, то найдется квадрат, в котором стоит не более двух фигур. Без ограничения общности можно считать, что это левый верхний квадрат (см. рис. 6).
Рассмотрим угловую клетку
X1, прилегающую к ней клетку X2 и клетку X3 по диагонали от угловой. Цифрами 1, 2 и 3 отметим клетки, которые бьет конь, если он стоит в клетках X1, X2 и X3 соответственно. Заметим, что эти три множества клеток (типа 1, типа 2 и типа 3) не пересекаются. Кроме того, если конь стоит в одной из клеток X1, X2 или X3, то ни на одну из фигур, стоящих вне рассматриваемого квадрата, он нападать не может.Таким образом
: 1) если обе белые фигуры стоят в клетках одного типа, например, типа 2, ставим черного коня либо в клетку X1, либо в клетку X3; 2) если белые фигуры стоят в клетках разного типа, например, 1 и 2, то ставим коня в клетку X3; 3) если обе белые фигуры стоят в двух клетках, отмеченных знаком Xk, то ставим коня в третью клетку, отмеченную таким знаком. Случаи, когда одна фигура стоит в клетке, отмеченной знаком Xk, а другая – в какой-то другой клетке, сводятся к уже разобранным.