11 класс.
1.1.
Числа x и y таковы, чтоОтвет
: ± 1.Первый способ
. Из условия задачи следует, чтоЕсли
x = 2y, то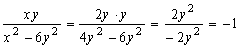 ; если x = 3y, то
; если x = 3y, то 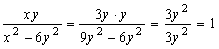 .
.
Второй способ
. Из условия следует, что у ¹ 0. Разделим числитель и знаменатель данной дроби на у2: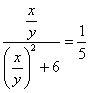 .
.
Пусть
1.2.
Боковые рёбра четырехугольной пирамиды имеют длины 1, 6 и 11. Может ли основание этой пирамиды быть квадратом?Ответ: нет, не может.
Предположим, что основанием данной пирамиды является квадрат
. Рассмотрим треугольник, стороны которого – боковые рёбра с длинами 1 и 6. Длина его третьей стороны, являющейся либо стороной, либо диагональю квадрата, меньше 7. В обоих случаях получим, что длина стороны квадрата меньше 7.Рассмотрим треугольник, стороны которого – боковые рёбра длины 1 и 11. Его третья сторона также является либо стороной, либо диагональю квадрата, поэтому ее длина должна быть меньше, чем
1.3.
На шахматной доске отмечены центры всех клеток. Рассмотрим все векторы, начало которых в центре черной клетки, а конец – в центре белой клетки. Докажите, что сумма этих векторов равна нулевому вектору.Для каждой черной клетки существует черная клетка, симметричная ей относительно центра доски. Аналогичное утверждение верно и для каждой белой клетки. Следовательно, каждому построенному вектору будет соответствовать вектор, ему центрально симметричный. Разобьем сумму всех рассматриваемых векторов на пары центрально симметричных векторов. Центрально симметричные вектора являются противоположными, поэтому сумма векторов в каждой паре равна нулевому вектору, следовательно и сумма всех векторов также равна нулевому вектору.
2.1.
Пусть f(x) – некоторая функция, определенная на всей числовой прямой. Известно, что функция f(f(x)) – непрерывная. Верно ли, что функция f(x) – непрерывная?Ответ
: нет, не верно.Приведем несколько примеров: 1) Функция
2) Функция
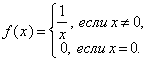 имеет разрыв в точке x = 0, при этом f(f(x)) = x для любых x, поэтому, функция f(f(x)) непрерывна на R.
имеет разрыв в точке x = 0, при этом f(f(x)) = x для любых x, поэтому, функция f(f(x)) непрерывна на R.
3) Функция Дирихле: ![]() не является непрерывной ни в одной точке! При этом f(f(x)) = 1 для любых x, поэтому, функция f(f(x)) – непрерывна на R.
не является непрерывной ни в одной точке! При этом f(f(x)) = 1 для любых x, поэтому, функция f(f(x)) – непрерывна на R.
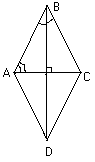
2.2. ABCD – ромб. Радиус окружности, описанной около треугольника АВC, равен 3 см, а радиус окружности, описанной около треугольника BDC, равен 4 см. Найдите периметр ромба.
Ответ: 19, 2 см.
Первый способ. Пусть Ð
ВАС = a
, тогда Ð
СBD = Ð
ABD = 90°
– a
(см. рис. 1). Пусть R1 и R2 – радиусы окружностей, описанных около треугольников АВC и ВDC соответственно. Тогда, по следствию из теоремы синусов для D
АВС: ВC = 2R1×
sina
. Аналогично, для D
ВСD: CD = 2R2×
sin(90°
– a
) = 2R2×
cosa
. Так как ВC = CD = a, то tga
= ![]() . При заданных числовых значениях: tga
=
. При заданных числовых значениях: tga
= ![]() ; cosa
=
; cosa
= ![]() ; a = 4,8 (см); РABCD = 19, 2 (см).
; a = 4,8 (см); РABCD = 19, 2 (см).
Можно также получить соотношение между стороной ромба и данными радиусами в явном виде: 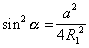 ;
; 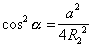 ; тогда
; тогда 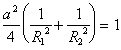 , то есть,
, то есть,
a = ![]() .
.
Второй способ
. Очевидно, что2.3.
Найдите все натуральные значения n, для которых выполняется равенство: n3 – n = n!Ответ
: n = 5.Запишем данное уравнение в виде
n(n – 1)(n + 1) = n(n – 1)(n – 2)(n – 3) × × × 2× 1. Так как n = 1 не является его решением, то разделим обе части уравнения на n(n – 1). Получим, что n + 1 = (n – 2)(n – 3)× ...× 2× 1. Проверяя последовательные натуральные значения n, начиная с n = 2, получим, что решением уравнения является n = 5.Так как для всех
n > 5 n + 1 < 2n – 4 = 2(n – 2), то n + 1 < (n – 2)× 2 < (n – 2)(n – 3)× ...× 2× 1, поэтому других натуральных решений данное уравнение не имеет.
3.1.
Решите уравнение:Ответ
: 0; 1.Пусть
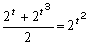 .
.
Воспользуемся дважды неравенством между средним арифметическим и средним геометрическим:
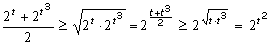 , причем равенство возможно тогда и только тогда, когда
, причем равенство возможно тогда и только тогда, когда Отметим, что возможно аналогичное решение без замены переменных.
3.2.
В равнобедренном треугольнике АВС на боковых сторонах АВ и BС взяты точки К и L так, что АК = BL. Докажите, что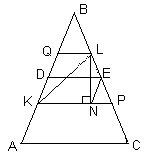
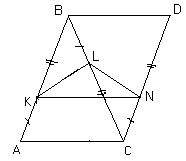
Первый способ
. Достроим данный треугольник АВС до параллелограмма ABDC и на стороне CD отложим отрезок CN = BL (см. рис. 2а). Тогда из равенства треугольников KBL и NCL следует, что LN = KL, а из того, что AKNC – параллелограмм, следует, что АС = KN. Применив неравенство треугольника для D KLN получим, что KL + LN ³ KN, то есть,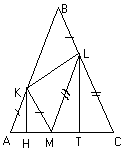
Второй способ Проведем
DE – среднюю линию треугольника АВС. Если KL совпадает с DE, тоТретий способ. Проведем
KM || BC (см. рис. 2в), тогда D AKM – равнобедренный, то есть, KM = AK = BL. Следовательно, KMLB – параллелограмм, то есть, ML || AB и ML = KB = LC.Проведём высоты
KH и LT в равнобедренных треугольниках AKM и MLC соответственно. Так как эти высоты являются медианами, то HT =Четвертый способ. Проведем
KH и LT – перпендикуляры к прямой АС (см. рис. 2в), тогда HT £ KL. Пусть Ð BAC = Ð BCA = a , тогда AH = AK× cosa , CT = CL× cosa . Следовательно, AH + CT = (AK + CL)× cosa = AB× cosa =3.3.
Решая числовой ребус ДВА + ТРИ = ПЯТЬ, Вася получил 150 возможных ответов. Верно ли, что Вася нашел все решения ребуса?Ответ
: нет, не верно.Пусть найдено какое-то решение данного ребуса. Тогда существуют еще три решения этого ребуса, которые получаются из него следующим образом: 1) перестановкой числовых значений букв А и И; 2) перестановкой числовых значений букв В и Р; 3) осуществлением обеих перестановок. Отметим, что перестановка числовых значений букв Д и Т в решении ребуса не приводит к новому решению, так как буква Т присутствует еще и в правой части равенства.
Рассмотрим множество решений данного ребуса и разобьем его на четыре непересекающихся подмножества: 1) В > Р и А > И; 2) В > Р и А < И; 3) В < Р и А > И; 4) В < Р и А < И (неравенства – строгие, так как различным буквам должны соответствовать различные цифры). Каждому решению из одного подмножества соответствует ровно одно решение из любого другого подмножества и эти соответствия взаимно однозначны, поэтому эти подмножества содержат равные количества элементов.
Следовательно, общее количество решений ребуса должно быть кратно 4, а число 150 на 4 не делится.
С помощью компьютера можно найти все решения данного ребуса. Оказывается, что их – 180.
4.1. Найдите значение выражения: (1 + tg1° )× (1 + tg2° )× ...× (1 + tg44° ).
Ответ
: 222.Так как
Таким образом,
4.2.
По горизонтальной прямой s произвольным образом «катаются» две окружности, радиусы которых r и R. К ним проведены две общие внутренние касательные, пересекающиеся в точке M. По какой траектории движется точка M?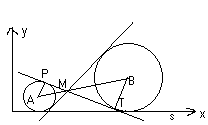
Ответ
: по прямой, параллельной s и находящейся от нее на расстоянииПусть А и В – центры данных окружностей;
P и T – точки касания окружностей с одной из данных касательных (см. рис. 3а). Так как при гомотетии с центром М одна из окружностей переходит в другую, то М лежит на прямой АВ. Кроме того, AM : MB = r : R (это соотношение можно также получить из подобия треугольников APM и BTM).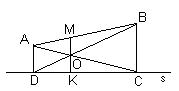
Введем на плоскости декартову систему координат так,
чтобы прямая s являлась осью абсцисс. Тогда точка A движется по прямой y = r; а точка B – по прямой y = R. В этом случае:Этот же результат можно получить геометрически. Опустим перпендикуляры
AD и ВС на прямую s (см. рис. 3б). Пусть диагонали АС и BD трапеции АВСD пересекаются в точке О. Длина отрезка MK, содержащего точку О и параллельного основаниям трапеции, является средним гармоническим длин оснований, то есть,4.3.
На столе лежат три кучки камней, в одной из которых 5 камней, в другой – 49, а в третьей – 51. Разрешается делать две операции: 1) складывать любые две кучки камней в одну; 2) любую кучку с четным количеством камней делить на две равные кучки. Можно ли, выполняя только эти операции, разложить камни на кучки по одному?Ответ
: нет, нельзя.Так как количество камней в каждой кучке нечетно, то сначала придется сложить какие-либо две кучки в одну. Рассмотрим возможные варианты:
1) Сложим в одну кучки из 5 камней и 49 камней. Получим две кучки: 54 камня и 51 камень. Оба количества камней кратны трем. Так как числа 3 и 2 взаимно просты, то при дальнейшем применении разрешенных операций могут получаться только кучки, количество камней в которых также кратно трем. Следовательно, количество камней в любой кучке не может стать меньше трех и разложить камни на кучки по одному невозможно.
2) Сложим в одну кучки из 5 камней и 51 камня. Получим две кучки: 56 камней и 49 камней. Оба количества камней кратны семи. Аналогичными рассуждениями получим, что количество камней в любой кучке не может стать меньше семи, что также не позволит разложить камни их в кучки по одному.
3) Сложим кучки из 49 камней и 51 камня. Получим две кучки: 100 камней и 5 камней. Оба количества камней кратны пяти, что также не позволит разложить их в кучки по одному камню.
5.1.
Известно, что для чисел а, b и с выполняются равенства: а3 – b3 – c3 = 3abc и а2 = 2(b + c). Найдите число а.Ответ
: 0; 2; –4.Рассмотрим выражение
x3 + y3 + z3 – 3xyz и разложим его на множители: x3 + y3 + z3 – 3xyz = (x + y)(x2 – xy + y2) + z3 – 3xyz = (x + y)((x + y)2 – 3xy) + z3 – 3xyz = (x + y)3 + z3 – 3xy(x + y) – 3xyz = (x + y + z)((x + y)2 – (x + y)z + z2) – 3xy(x + y + z) = (x + y + z)(x2 + y2 + z2 – xy – yz – zx).Заметим также, что выражение во второй скобке может принимать только неотрицательные значения, то есть,
x2 + y2 + z2 ³ xy + yz + zx, причем равенство достигается тогда и только тогда, когда x = y = z.Это можно доказать различными способами, например: 1)
x2 + y2 + z2 – xy – yz – zx = 0,5(2x2 + 2y2 + 2z2 – 2xy – 2yz – 2zx) = 0,5((x – y)2 + (y – z)2 + (z – x)2) ³ 0; 2) записав три верных неравенства:Пусть
x = a, y = –b, z = –c, тогда a3 – b3 – c3 – 3abc = (a – b – c)(a2 + b2 + c2 + ab – bc + ca). По доказанному выше, равенство а3 – b3 – c3 = 3abc выполняется если a = b + c или а = –b = –c.Из равенства а
2 = 2(b + c) в первом случае получим, что a2 = 2a Û a = 0 или a = 2, а во втором случае: a2 = –4a Û a = 0 или a = –4.Отметим, что если само тождество
x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx) известно, то доказать его можно и проще: раскрыть скобки в правой части и привести подобные слагаемые.Также можно было преобразовывать первое из данных равенств, используя, например, замену переменных: u = b + c, v = bc. Так как
b3 + c3 = (b + c)(b2 – bc + c2) = (b + c)((b + c)2 – 3bc), то это равенство примет вид: a3 – (u3 – 3uv) = 3av Û (a – u)(a2 + au + u2) + 3v(u – a) = 0 Û (a – u)(a2 + au + u2 – 3v) = 0. Выполнив обратную замену, получим, что (a – b – c)(a2 + b2 + c2 + ab – bc + ca) = 0. Дальнейшее решение совпадает с уже изложенным.5.2.
Площадь ортогональной проекции некоторого параллелепипеда на плоскость одной из его граней в два раза больше площади этой грани, площадь его ортогональной проекции на плоскость другой грани в полтора раза больше площади этой грани, и наконец, площадь его проекции на плоскость третьей грани равна площади этой грани. Найдите плоские углы в гранях данного параллелепипеда.Ответ: в четырех гранях все углы по 90° ; в двух гранях –- 45° и 135°
.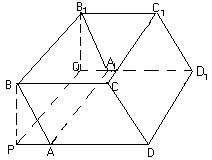
Рассмотрим ортогональную проекцию параллелепипеда АВС
DA1B1C1D1 на плоскость грани АВСD. Пусть площадь этой проекции равна площади АВСD, тогда эта грань является проекцией грани A1B1C1D1, то есть, ребра AA1, BB1, CC1 и DD1 перпендикулярны рассматриваемым граням. Следовательно, грани АВВ1А1, ВВ1С1С, СС1D1D и DD1A1A являются прямоугольниками (см. рис. 4).Пусть
PQD1D – ортогональная проекция параллелепипеда на плоскость грани AA1D1D.Ð
PAB = a
– острый угол в грани ABCD, который является углом между плоскостями граней ABB1A1 и АВСD. Угол между плоскостями параллельных им граней СС1В1В и СС1D1D также равен a
, поэтому рассматривая проекцию параллелепипеда на плоскость СС1D1D аналогично получим, что площадь этой проекции равна ![]() .
.
По условию, найденные площади соответственно равны
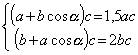 . Упростим ее:
. Упростим ее: Отметим, что после того, как было доказано, что четыре грани параллелепипеда являются прямоугольниками, мы практически рассматривали не ортогональные проекции этого параллелепипеда на плоскости граней, а ортогональные проекции параллелограмма АВС
D на прямые AD и CD.5.3. На доске было записано 17 двузначных чисел. Математик выбрал одно из них и возвел его в сотую степень. Оказалось, что полученное число делится на каждое из оставшихся шестнадцати. Верно ли, что оно делится и на их произведение?
Ответ
: верно.Если двузначное число n разложить в произведение простых множителей, то есть, представить в виде: n = ![]() , то
, то ![]() 6. Действительно, наименьшим простым множителем является число 2, а максимальным показателем степени в разложении может быть 6, так как 26 = 64 < 100, а 27 = 128 > 100.
6. Действительно, наименьшим простым множителем является число 2, а максимальным показателем степени в разложении может быть 6, так как 26 = 64 < 100, а 27 = 128 > 100.
Рассмотрим выбранное число т в сотой степени. По условию т
100 кратно каждому из оставшихся чисел n1, n2, … n16, следовательно, т100 кратно каждому простому делителю любого из этих чисел, причем в разложение числа т100 каждый из этих простых делителей входит с показателем степени, не меньшим ста.Разложение произведения
n1× n2 × × × n16 на простые множители содержит те же множители, причем показатель степени каждого из них не превосходит 16× 6 = 96 < 100. Значит, т100 делится на n1× n2 × × × n16, что и требовалось доказать.