1.1.
Докажите, чтоТак как
1.2.
Из вершины А параллелограмма АВСD проведены высоты AK и AM. Может ли оказаться так, что точка K лежит на стороне параллелограмма, а точка М – на продолжении стороны?Ответ
: да, может (см. рис. 1).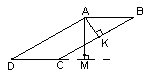
Отметим, что в любом параллелограмме, не являющемся прямоугольником, основания высот, проведенных из вершины острого угла, лежат на продолжениях сторон, а основание одной из высот, проведенных из вершины тупого угла, может попасть на продолжение стороны параллелограмма, если угол между меньшей диагональю и одной из сторон – тупой.
1.3. Существуют ли три последовательных натуральных числа, каждое из которых делится на квадрат какого-нибудь натурального числа, отличного от единицы?
Ответ
: да, существуют.Приведем несколько примеров: 1)
48 = 3× 42; 49 = 72; 50 = 2× 52; 2) 98 = 2× 72, 99 = 11× 32, 100 = 22× 52; 3) 124 = 31× 22, 125 = 53, 126 = 14× 32.Указанные «тройки» чисел – наименьшие из возможных
.
2.1.
Числа a, b, c и d таковы, что a + b = c + d и a2 + b2 = c2 + d2. Верно ли, что a3 + b3 = c3 + d3?Ответ
: верно.Если a + b = c + d, то (a + b)2 = (c + d)2 Û a2 + 2ab + b2 = c2 + 2cd + d2, откуда, учитывая что a2 + b2 = c2 + d2, получим, что ab = cd.
Далее возможны различные способы, например:
1) a3 + b3 = (a + b)(a2 – ab + b2) = (c + d)(c2 – cd + d2) = c3 + d3.
2) Так как
a + b = c + d Û (a + b)3 = (c + d)3 Û a3 + b3 + 3ab(a + b) = c3 + d3 + 3cd(c + d), то a3 + b3 = c3 + d3.
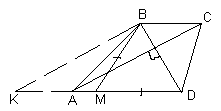
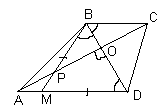
2.2. В трапеции АВСD диагонали АС и BD перпендикулярны. На большем основании AD выбрана точка М так, что BM = MD = 3 см. Найдите длину средней линии трапеции.
Ответ: 3 см.
Первый способ. Проведем прямую через вершину В, параллельную АС, которая пересечет прямую АD в точке K (см. рис. 2а). Тогда D KВD – прямоугольный, М лежит на его гипотенузе KD и равноудалена от вершин В и D, следовательно М – середина KD. Так как ВСАК – параллелограмм, то ВС = АК. Следовательно, длина средней линии составляет половину длины KD, то есть, равна 3 см.
Второй способ. Пусть О – точка пересечения диагоналей трапеции; Р – точка пересечения ВМ и АС (см. рис. 2б). По условию, D BMD – равнобедренный, значит, Ð MBD = Ð MDB = a . Так как Ð CBD = Ð MDB = a и ВО ^ РС, то ВО – высота и биссектриса треугольника РВС, поэтому, этот треугольник – также равнобедренный, то есть, ВР = BC.
Так как Ð
APM = Ð BPO = 90° – a = Ð OAD, то равнобедренным является и треугольник АМР: АМ = PM. Таким образом, средняя линия трапеции равна:![]() =
= ![]() =
= ![]() =
=
2.3.
В круговом турнире каждый участник встретился с каждым один раз (победа – 1 очко, ничья – 0,5 очка, поражение – 0). Единоличным победителем турнира стал Иванов. Затем за употребление допинга был дисквалифицирован Петров, результаты всех игр с его участием были аннулированы, и единоличным победителем оказался Сидоров. Петров утверждает, что если бы дисквалифицировали не его, а Сидорова, то он (Петров) стал бы единоличным победителем. Может ли это быть правдой?Ответ: нет, не может.
До дисквалификации Петрова Иванов опережал Сидорова не
менее чем на пол-очка, а после – уступил ему не менее, чем пол-очка. Следовательно, Иванов выиграл у Петрова. Так как после дисквалификации Сидоров опередил Иванова, то при пересчете Сидоров очков не терял, значит, Сидоров проиграл Петрову. Следовательно, при дисквалификации Сидорова Петров потеряет одно очко и опередить Иванова не сможет (даже если Иванов выиграл у Сидорова и также потеряет это очко).
3.1.
Решите уравнение: 2x2 + 5y2 – 4xy – 2y – 4x + 5 = 0.Ответ
: x = 2; y = 1.Преобразуем данное уравнение: (
x2 – 4xy + 4y2) + (x2 – 4x + 4) + (y2 – 2y + 1) = 0 Û (x – 2y)2 + (x – 2)2 + (y – 1)2 = 0. Так как каждое слагаемое в левой части принимает только неотрицательные значения, то полученное равенство выполняется тогда, и только тогда, когда каждое слагаемое равно нулю: (y – 1)2 = 0 Û y = 1; (x – 2)2 = 0 Û x = 2; (x – 2y)2 = 0 Û x = 2y. При x = 2, y = 1, последнее равенство верно.
3.2.
В прямоугольнике АВСD точка М – середина стороны ВС, точка N – середина стороны СD, Р – точка пересечения отрезков DМ и ВN. Докажите, что Ð МАN = Ð ВРМ.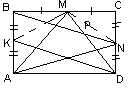
Первый способ
. Пусть К – середина стороны АВ (см. рис. 3). Тогда, так как BK || ND и BK = ND, то KBND – параллелограмм. Следовательно, KD || BN, то есть, Ð ВРМ = Ð KDM.Соединим точку М
c точками N и K. Так как D KDM = D NAM (по трем сторонам), то Ð KDM = Ð MAN. Следовательно, Ð ВРМ = Ð MAN, что и требовалось доказать.Второй способ. Так как
AM = MD и BC || AD, то Ð MAD = Ð MDA = Ð DMC (см. рис. 3). Кроме того, из равенства прямоугольных треугольников ВСN и ADN следует, что Ð NBM = Ð NAD.По теореме о внешнем угле для D ВМР
: Ð BPM = Ð DMC – Ð NBM = Ð MAD – Ð NAD = Ð MAN, что и требовалось доказать.
3.3.
У Золотой рыбки записаны и перенумерованы подряд все знакомые. Половина из них – щуки, треть – окуни, а все знакомые с номерами, делящимися на 4, – караси. Сколько всего знакомых у Золотой рыбки?Ответ: 6 знакомых.
Первый способ
. Выпишем в ряд всех знакомых Золотой рыбки и разделим их на части, учитывая, что все знакомые с номерами, делящимися на 4, – караси (К – карась, Р – другая рыба):Р Р Р К Р Р
| Р К Р Р Р | К Р Р Р | К Р Р Р | К Р Р Р | ... (все части, начиная с третьей, – одинаковые, но в последней части может быть и менее четырех знакомых).Тогда в первой части караси составляют
Второй способ
. Из условия следует, что количество знакомых Золотой рыбки является числом вида 6n, где n – натуральное; из них: 3n щук и 2n окуней, поэтому карасей – не больше, чем n.Пусть
Третий способ
. Заметим, что количество знакомых Золотой рыбки не может быть кратно четырем, так какОбщее количество щук, карасей и окуней не превосходит общего количества знакомых, следовательно,
4.1.
Верно ли, что все корни уравненияОтвет
: да, верно.![]() Û
Û
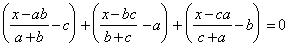 Û
Û
![]() Û
Û
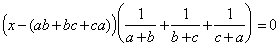 .
.
Из условия следует, что второй множитель – положительное число, значит,
x – (ab + bc + ca) = 0 Û x = ab + bc + ca, то есть, x – целое число.Эту же идею можно реализовать иначе
:Отметим, что попытки непосредственного умножения обеих частей уравнения на общий знаменатель левой части приводят к очень громоздким преобразованиям.
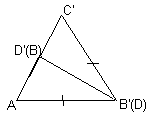
4.2.
В выпуклом четырехугольнике АВСD: АD = ВС; Ð ABD + Ð CDB = 180° . Докажите, что Ð BАD = Ð ВCD.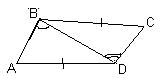
Разрежем данный четырехугольник по диагонали ВD (см. рис. 4а) и, «перевернув» треугольник ВСD, вновь приложим его к диагонали ВD (см. рис.
4б). Получился равнобедренный треугольник АB’C’ (АB’ = B’C’). Следовательно Ð B’АD’ = Ð В’C’D’, то есть, Ð BАD = Ð ВCD, что и требовалось доказать.Отметим, что выходя за рамки материала, уже изученного восьмиклассниками, можно предложить другой способ решения (см. рис. 4а).
Пусть Ð
AВD = a
, тогда Ð
СDB = 180°
– a
. По теореме синусов из D
AВD: ![]() . Аналогично, из D
ВСD:
. Аналогично, из D
ВСD: ![]() . Учитывая, что АD = ВС и sin(180°
– a
) = sina
, получим, что sinÐ
A = sinÐ
C.
. Учитывая, что АD = ВС и sin(180°
– a
) = sina
, получим, что sinÐ
A = sinÐ
C.
Так как Ð
ABD + Ð CDB = 180° , то либо каждый из этих углов – прямой, либо один из них – острый, а другой – тупой. В первом случае ясно, что углы А и С – острые, поэтому, из равенства их синусов следует равенство углов.Во втором случае, без ограничения общности
можно считать, что Ð ABD = a – острый, а Ð CDB – тупой. Тогда Ð С – острый, следовательно, из D ВСD получим, что BD < BC. Предположим, что Ð А – не острый, тогда в D AВD: Ð А > a , то есть, BD > AD. Значит, BC > AD, что противоречит условию.Таким образом, Ð А – острый, поэтому Ð А
= Ð C, что и требовалось доказать.
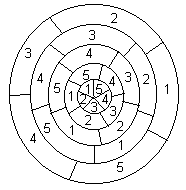
4.3.
Дан круг радиуса 10см. На одном из его радиусов отмечены пять точек: на расстояниях 1, 3, 5, 7 и 9 см от центра соответственно. Разрежьте этот круг на 5 равных частей так, чтобы в каждой части оказалась ровно одна точка.Проведем четыре концентрические окружности с тем же центром и радиусами 2, 4, 6 и 8 см. Затем разрежем самый маленький круг и каждое из четырех полученных колец на 5 равных частей (см. рис. 5, «кусочки» одной части пронумерованы одинаково). Очевидно, что при таком разрезании существует радиус данного круга, пересекающий все полученные части, на котором и расположены данные точки.