9 класс.
1.1.
Даны два квадратных трехчлена, сумма коэффициентов каждого из которых равна 1. Эти трехчлены перемножили и получили многочлен. Найдите сумму его коэффициентов.Ответ
: 1.Воспользуемся тем, что сумма коэффициентов
произвольного многочлена1.2.
Каждая из высот параллелограмма не меньше той стороны, которой она перпендикулярна. Найдите угол между диагоналями параллелограмма.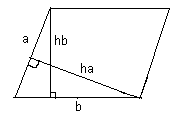
Ответ
: 90° .Пусть
a и b – длины сторон параллелограмма, а ha и hb – длины проведенных к ним высот. По условию, ha ³ a и hb ³ b. Кроме того, a ³ hb и b ³ ha (см. рис. 1). Таким образом, ha ³ a ³ hb ³ b ³ ha, следовательно, ha = a = hb = b. Это означает, что данный параллелограмм является квадратом, то есть, угол между диагоналями – прямой.1.3.
Турнир по боксу проходил по «олимпийской системе» (в каждом круге проигравшие выбывают). Сколько боксеров участвовало в турнире, если по окончании турнира выяснилось, что 32 человека выиграло боев больше, чем проиграло?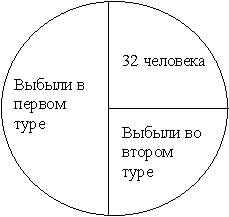
Ответ
: 128.Участники, выбывшие после первого круга, проиграли по одному бою и не выиграли ни одного. Участники, выбывшие после второго круга, по одному бою выиграли и по одному бою проиграли. Поэтому боксеры, которые выиграли больше боев, чем проиграли – это те, которые выиграли хотя бы по два боя, то есть прошли в третий круг. Во второй круг прошла половина участников, а в третий – четверть (см. рис. 2). Следовательно, 32 человека составляют четверть от всех участников турнира, а общее количество боксеров равно 128.
2.1.
Известно, что положительные числа a и b удовлетворяют неравенству:Так как а +
b > 0, то данное неравенство равносильно неравенству2.2.
Можно ли разрезать прямоугольный треугольник с углом 30° на подобные непрямоугольные треугольники?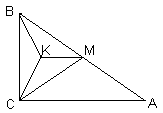
Ответ
: да, можно.Пусть АВС – данный треугольник, в котором Ð BAC = 30° . Проведем медиану CM, после чего точку K – центр равностороннего треугольника ВСМ соединим с его вершинами (см. рис. 3). Треугольники АМС, MKC, BKM и CKB – равнобедренные с углом 120° при вершине, поэтому являются подобными.
2.3.
Сколько существует не равных между собой треугольников, длины сторон которых – натуральные числа, а периметр равен 20?Ответ
: 8.Пусть а
, b и с – длины сторон треугольника (a ³ b ³ c). Докажем, что 6 < a < 10. Предположим, что a £ 6, тогда b £ 6 и с £ 6, то есть, Р = a + b + c < 20 – противоречие. Предположим, что a ³ 10, тогда b + c > a ³ 10, то есть, Р > 20 – противоречие.|
a |
9 |
9 |
9 |
9 |
8 |
8 |
8 |
7 |
|
b |
9 |
8 |
7 |
6 |
8 |
7 |
6 |
7 |
|
c |
2 |
3 |
4 |
5 |
4 |
5 |
6 |
6 |
Все возможные треугольники, у которых большая сторона имеет длину 9, 8 или 7, находим перебором (см. таблицу).
3.1.
Дан квадратный трёхчлен ax2 + bx + c, все коэффициенты которого отличны от нуля. Ваня и Петя должны найти количество его корней. Ваня случайно поменял местами коэффициенты a и b и получил, что трехчлен имеет один корень. Петя вместо этого поменял местами b и c и также получил, что корень – один. Сколько корней у трёхчлена на самом деле?Ответ
: 0.Так как трехчлен
bx2 + ax + c имеет один корень, то a2 – 4bc = 0 Û a2 = 4bc. Аналогично, так как трехчлен ax2 + сx + b также имеет один корень, то c2 – 4ab = 0 Û c2 = 4ab. Перемножив полученные равенства и разделив обе части на ас, получим, что ас = 16b2.Дискриминант данного трехчлена:
D = b2 – 4ac = b2 – 64b2 = –63b2 < 0 при b ¹ 0. Следовательно, данный трехчлен корней не имеет.Можно доказать, что любой трехчлен, удовлетворяющий условию задачи, имеют вид
: 4kx2 + kx + 4k, где k ¹ 0.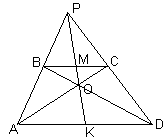
3.2.
Дана трапеция, основания которой имеют длины 4 и 5. Пользуясь только односторонней линейкой (без делений), постройте отрезок длины 1.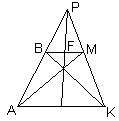
Пусть АВС
D – данная трапеция, причем ВС = 4. Воспользуемся тем, что в любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой (это можно доказать, используя, например, векторы или гомотетию).Проведем диагонали трапеции АС и
BD (O – точка их пересечения) и продолжим боковые стороны до пересечения в точке Р (см. рис. 4а). Тогда прямая ОР пересечет основания трапеции в их серединах, точках M и K, поэтому ВМ = 2. Выполнив аналогичное построение, например, для трапеции АВМK, получим, что BF = FM = 1 (см. рис. 4б).3.3.
Из простого двузначного числа вычли число, записанное теми же цифрами, но в обратном порядке, которое также оказалось простым, и получили квадрат натурального числа. Каким могло быть исходное число?Ответ
: 73.Пусть исходное число
4.1.
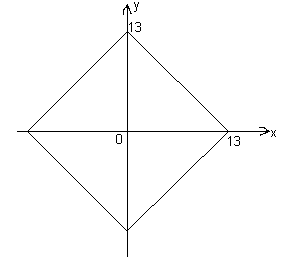
Найдите наибольшее и наименьшее значение выражения y – x2, если ú xú + ú yú £ 13.Ответ
: наибольшее значение равно 13, а наименьшее значение равно –169.Построим график уравнения ú xú + ú yú = 13, тогда данному неравенству удовлетворяют координаты всех точек, принадлежащих этому графику и точек, лежащих внутри ограниваемой им области (см. рис. 5).
Пусть y – x2 = t, тогда решение задачи сводится к тому, чтобы найти наибольшее и наименьшее значения переменной t, для которых график функции y = x2 + t имеет общие точки с найденным множеством.
Так как график указанной функции получается из параболы y = x2 параллельным переносом вдоль оси y, то: 1) наибольшее значение t достигается, если вершиной параболы y = x2 + t является точка (0; 13), то есть, при t = 13; 2) наименьшее значение t достигается, если парабола y = x2 + t проходит через точки (13; 0) и (–13; 0), то есть, при t = –169.
4.2. Даны треугольник АВС и точки D и Е такие, что Ð АDВ = Ð ВЕС = 90° . Докажите, что длина отрезка DE не превосходит половины периметра треугольника АВС.
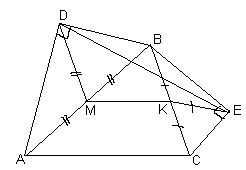
Пусть М и
K – середины сторон АВ и ВС данного треугольника АВС соответственно (см. рис. 6а). Тогда DM – медиана прямоугольного треугольника АDВ, проведенная к гипотенузе, то есть, DM = 0,5AB. Аналогично, так как EK – медиана треугольника ВЕС, то EK = 0,5BC. MK – средняя линия треугольника АВС, значит, MK = 0,5AC. Так как длина ломаной не меньше длины отрезка, соединяющего ее концы, то DE £ DM + MK + KE = 0,5(AB + AC + BC) = 0,5PABC, что и требовалось доказать.Те же идеи можно реализовать и по другому
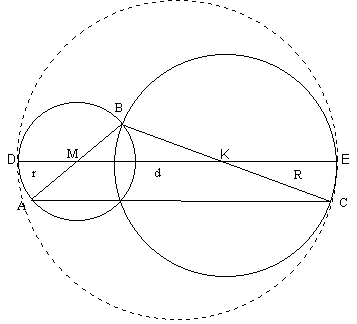
.Пусть
R и r – радиусы окружностей, построенных на сторонах АВ и ВС данного треугольника, как на диаметрах, а d – длина средней линии MK (см. рис. 6б). Тогда полупериметр треугольника АВС равен:Из условия следует, что точки
D и E лежат на окружностях с центрами М и K соответственно, поэтому, расстояние DE будет наибольшим, если эти точки являются точками попарного касания окружностей. В этом случае, DE – диаметр большой окружности, причем,4.3.
Может ли число, десятичная запись которого содержит более одной цифры, равняться произведению своих цифр?Ответ
: нет, не может.Рассмотрим произвольное n – значное число, где n ³
2: ![]() ³
³
![]() ³
³
![]() >
> ![]() , так как каждый сомножитель в скобках меньше 10.
, так как каждый сомножитель в скобках меньше 10.
5.1.
Найдите, какие значения может принимать суммаОтвет
: 2.![]() Û
Û
![]() Û
Û
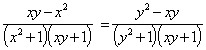
Тогда
5.2.
В выпуклом четырехугольнике АВСD: Ð ABD = Ð CDB = 60° , Ð ВСA = Ð CАD = 30° . Найдите ВD, если АВ = 2 см.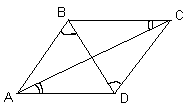
Ответ: 2 см
или 4 см.Из условия следует, что АВС
D – параллелограмм. Рассмотрим осевую симметрию относительно прямой BD, при которой образом точки А является точка А’. Тогда ВА’ = BA; DА’ = DA; Ð А’BD = Ð ABD = 60° ; Ð BА’A = Ð BAA’ = 30° . Возможны два случая:1) Точка А
’ совпала с точкой С (см. рис. 7а).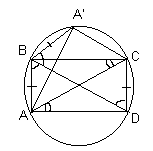
Тогда,
ABCD – ромб с острым углом 60° , значит, ВD = AB = 2 (см).2) Точка А
’ не совпала с точкой С. Так как Ð ABD – острый, то отрезок АA’ пересекает луч BD (см. рис. 7б).В этом случае рассмотрим окружность, описанную около треугольника АВС. Точка А
’ лежит на этой окружности, так как Ð ВА’А = Ð ВСА, а точка D – поскольку ВD и А’C – основания равнобокой трапеции. Следовательно, Ð BDA = Ð ВСА = 30° , поэтому, АВСD – прямоугольник.Из прямоугольного треугольника АВ
D, в котором Ð BDA = 30° , находим, что BD = 2AB = 4 (см).Для тех
учащихся 9 классов, кто знаком с простейшими тригонометрическими формулами, можно предложить другой способ решения, использующий теорему синусов.Пусть О – точка пересечения диагоналей параллелограмма АВС
D и Ð ADB = a . Тогда Ð AOB = 30° + a ; Ð BAC = 90° – a .Из D
AOD:Аналогичные соотношения можно получить, если использовать равновеликость треугольников
AOD и AOB, дважды вычислив их площади по формуле5.3.
Даны 70 различных натуральных чисел, каждое из которых не превосходит 200. Докажите, что хотя бы два из них отличаются на 4, 5 или 9.Предположим, что это не так. Пусть
В этом наборе 210 натуральных чисел, все они различны (по нашему предположению) и самое большое из них не превосходит 200 + 9 = 209.
Получено противоречие (принцип Дирихле
!), поэтому хотя бы два из данных чисел отличаются на 4, 5 или 9, что и требовалось доказать.