1.1. Решите уравнение: 2^|x| – cosy + lg(1 + x² + |y|) = 0.

Ответ: (0; 0).

Удобнее записать уравнение так: 2^|x| + lg(1 + x² + |y|) = cosy. Тогда 2^|x| ³ 2⁰ = 1 и lg(1 + x² + |y|) ³ lg1 = 0, то есть 2^|x| + lg(1 + x² + |y|) ³ 1. Так как cosy £ 1, то исходное уравнение равносильно системе: , причем равенства достигаются тогда и только тогда, когда они достигаются во всех записанных неравенствах. Следовательно, x = 0; y = 0.

1.2. В выпуклом четырехугольнике ABCD точки K, M, N и P – середины сторон AB, BC, CD и DA соответственно. Отрезки AM и CK пересекаются в точке E, а отрезки AN и CP – в точке F. Найдите площадь четырехугольника AECF, если площадь ABCD равна 12.

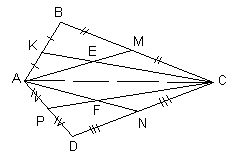
Ответ: 4.

Проведем диагональ AC данного четырехугольника (см. рис. 1). Тогда Е – точка пересечения медиан треугольника АВС. Так как медианы треугольника разбивают его на шесть равновеликих треугольников, то .

Аналогично, так как F – точка пересечения медиан треугольника АDС, то . Таким образом, = 4.

1.3. Пусть M – наименьшее из четырех чисел: a, b, c и 1 – а – b – c. Найдите наибольшее значение M.

Ответ: .

Пусть d = 1 – а – b – c, тогда из условия задачи следует, что a + b + c + d = 1. Предположим, что M > , тогда каждое из данных чисел больше, чем , следовательно, a + b + c + d > 1 – противоречие. Значение М = достигается, если а = b = c = d = .

 

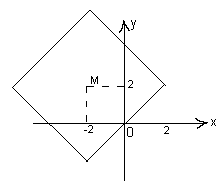
2.1. Найдите все значения k и b такие, что система уравнений 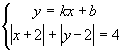имеет бесконечное множество решений.

Ответ: (1; 0); (1; 8); (–1; –4); (–1; 4).

Уравнение |x + 2| + |y – 2| = 4 задает на координатной плоскости контур квадрата с центром М(–2; 2) (см. рис. 2). Стороны этого квадрата принадлежат прямым, имеющим уравнения: y = x; y = x + 8; y = –x – 4; y = –x + 4.

Такие прямые имеют с границей построенного квадрата бесконечно много общих точек, а никакие другие прямые этим свойством не обладают. Таким образом, исходная система уравнений будет иметь бесконечно много решений тогда и только тогда, когда прямая y = kx + b совпадет с одной из этих четырех прямых. Следовательно, k = 1; b = 0 или k = 1; b = 8 или k = –1; b = –4 или k = –1; b = 4.

2.2. Существует ли невыпуклый многогранник, имеющий ровно пять вершин?

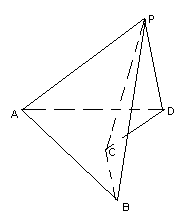
Ответ: да, существует.

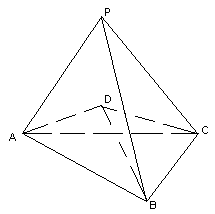
Например, пирамида РАВСD, основанием которой является невыпуклый четырехугольник АВСD (см. рис. 3а), или многогранник РАВСD, который получится, если из тетраэдра РАВС «вырезать» тетраэдр DABC (см. рис. 3б).

2.3. Докажите, что если числа m и m² + 2 – простые, то и число m³ + 2 – также простое.

Первый способ. Если число m – простое, то оно либо равно 3, либо не делится на 3.

Если m = 3, то m² + 2 = 11, m³ + 2 = 29, то есть эти числа – простые. Если число m не делится на 3, то остаток от его деления на 3 равен либо 1, либо 2. В обоих случаях остаток от деления числа m² на 3 равен 1, поэтому m² + 2 делится на 3. Так как это число – простое, то оно равно 3, тогда m = 1 – не простое, что противоречит условию задачи.

Второй способ. Если число m – простое и m > 3, то m = 6k ± 1, где kÎ N. Тогда m² + 2 = 36k² ± 12k +3, то есть m² + 2 делится на 3. Так как это число больше трех, то оно не является простым. Оставшиеся случаи: 1) если m = 2, то m² + 2 = 6 – не простое; 2) если m = 3, то m² + 2 = 11 – простое, тогда m³ + 2 = 29 – также простое число.

3.1. Докажите, что существуют различные действительные числа x, y и z такие, что x³ – 3x² = y³ – 3y² = z³ – 3z². Найдите все значения, которые может принимать сумма x + y + z таких чисел.

Ответ: 3.

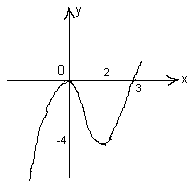
Пусть f(t) = t³ – 3t², тогда числа x, y и z – различные корни уравнения f(t) = a, где a – некоторое действительное число. Докажем, что это уравнение может иметь три различных действительных корня. Для этого исследуем функцию f(t) на монотонность и экстремумы и построим эскиз ее графика.

Так как f’(t) = 3t² – 6t = 3t(t – 2), то t = 0 и t = 2 – критические точки функции; f(0) = 0; f(2) = –4. Учитывая изменения знака производной, получим эскиз графика (см. рис. 4). Поэтому при аÎ (–4; 0) уравнение имеет три действительных корня, что и требовалось доказать.

Тогда по теореме Виета сумма x + y + z корней уравнения t³ – 3t² – а = 0 равна 3.

3.2. АМ – биссектриса равнобедренного треугольника АВС с основанием АС. Докажите, что если Ð В = 100° , то АМ + ВМ = АС.

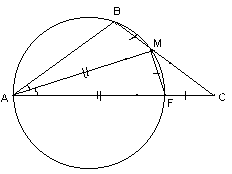
Первый способ. Из условия задачи следует, что Ð BMA = Ð MСA + Ð MAС = 60° . Отложим на продолжении биссектрисы AM отрезок ME, равный BM, и рассмотрим точку D, симметричную точке В относительно прямой АМ, лежащую на основании AC (см. рис. 5а). Тогда DM = BM = EM и Ð DMA = Ð BMA = 60° = Ð DMC = Ð EMC. Таким образом, МС – биссектриса Ð DME, поэтому углы МСD и МСЕ симметричны относительно прямой МС. Тогда в треугольнике АСЕ: Ð AСE = 80° = Ð AEC, то есть AC = AE = АМ + МE = АМ + ВМ, что и требовалось доказать.

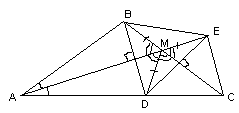
Второй способ. На основании АС данного треугольника отметим точку F такую, что AF = AM (см. рис. 5б). Тогда Ð AFM = Ð AMF = 80° . Так как Ð ABM + Ð AFM = 180° , то около четырехугольника АВМF можно описать окружность. Хорды ВМ и МF этой окружности равны, так как стягивают равные дуги. Кроме того, в треугольнике MFC: Ð MFC = 100° ; Ð MCF = 40° , поэтому Ð СMF = 40° . Следовательно, МF = FC. Таким образом, АМ + ВМ = АМ + МF = АF + FC = AC, что и требовалось доказать.

3.3. Можно ли из каких-нибудь девяти выпуклых шестиугольников составить какой-нибудь выпуклый тридцатидевятиугольник?

Ответ: нет, нельзя.

Пусть это возможно, тогда, так как 39-угольник составлен из шестиугольников, то его углы составлены из углов этих шестиугольников. Следовательно, сумма углов 39-угольника не превосходит суммы углов девяти шестиугольников. Но если эти многоугольники – выпуклые, то первая сумма равна 180° × 37, а вторая сумма равна (180° × 4)× 9 = 180° × 36.

4.1. Решите уравнение: .

Ответ: 2.

Заметим, что при x < 0 значение левой части больше, чем значение правой, поэтому данное уравнение не имеет отрицательных корней. Пусть x ³ 0, тогда запишем уравнение так: .

Для неотрицательных чисел справедливо неравенство: , причем равенство достигается при . Воспользуемся этим дважды, тогда: .

Таким образом, корнями уравнения являются те значения x, для которых в обоих случаях выполняются равенства. Следовательно, Û .

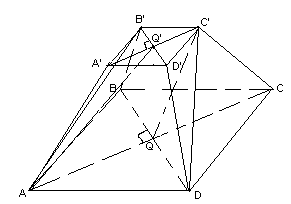
4.2. В правильной усеченной четырехугольной пирамиде проведено сечение через диагонали оснований, а также сечение, проходящее через ребро нижнего основания и противолежащее ребро верхнего основания. Найдите угол между секущими плоскостями, если площади данных сечений равны.

Ответ: 60° .

Пусть АВСDA’B’C’D’ – данная усеченная пирамида; AA’C’C и AB’C’D – равновеликие сечения; j – величина угла между их плоскостями (см. рис. 6). Проведем диагонали оснований, пересекающиеся в точках Q и Q’. Тогда ортогональной проекцией четырехугольника AB’C’D на плоскость AA’C’ является четырехугольник AQ’C’Q. По теореме о площади ортогональной проекции многоугольника: . Кроме того, , так как высоты этих трапеций равны, а основания первой трапеции – в два раза меньше соответствующих оснований второй. Следовательно, , то есть j = 60° .

Отметим, что «лобовые» способы вычисления искомого угла – весьма трудоемки.

4.3. На каждой половинке кости домино указано число очков – от 0 до некоторого N, большего 1. Все возможные пары чисел встречаются по одному разу (включая «дубли» – пары одинаковых чисел). Все кости домино выложены в цепочку, причем на прилегающих половинках соседних костей стоят одинаковые числа. Могут ли на концах цепочки стоять различные числа?

Ответ: нет, не могут.

Из условия задачи следует, что внутри цепочки числа должны стоять парами. Так как N > 1, то найдется число, не стоящее ни на одном из концов цепочки, то есть оно входит в цепочку четное количество раз. Кроме того, заметим, что все числа имеют одинаковое количество вхождений в цепочку, поэтому каждое из чисел входит в цепочку четное количество раз. Следовательно, если какое-то число стоит на одном конце цепочки, то оно же должно стоять и на другом конце.

Отметим, что каждое число входит в цепочку N + 2 раза. Так как N + 2 – четно, то и N – четно. Таким образом, если N > 1 и N – нечётно, то выложить в цепочку все кости домино невозможно.

5.1. Известно, что 9x² +16y² + 144z² = 169. Найдите наибольшее возможное значение выражения 6x – 4y + 24z.

Ответ: 39.

Рассмотрим векторы: (3x; 4y; 12z) и (2; –1; 2) такие, что = 6x – 4y + 24z. Тогда , . Так как , то 6x – 4y + 24z £ 39.

Равенство достигается тогда и только тогда, когда , то есть > 0 Û 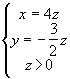. Подставив выражения для x и y в данное равенство получим, что найденное значение достигается, если ; ; .

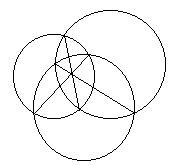
Полученный результат можно интерпретировать следующим образом. Данное уравнение задает в декартовой системе координат эллипсоид с центром О (0; 0; 0) (фигуру вращения эллипса вокруг одной из координатных осей). Из всех плоскостей вида 6x – 4y + 24z = d, где d > 0, ищется та плоскость, которая имеет с эллипсоидом общие точки и наиболее удалена от начала координат. Это будет плоскость, касательная к эллипсоиду.

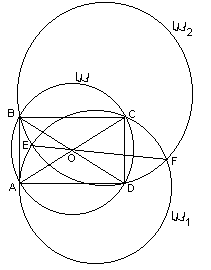
5.2. Одна окружность проходит через вершины A и C прямоугольника ABCD, другая – через вершины B и D. Докажите, что их общая хорда проходит через центр прямоугольника.

Решение этой задачи опирается на следующий факт. Пусть даны три окружности, которые пересекаются попарно, и существуют точки, принадлежащие всем трем кругам. Тогда три общие хорды этих окружностей пересекаются в одной точке (см. рис. 7а). Это утверждение можно доказывать различными способами.

«Планиметрическое» доказательство. Пусть дана окружность w и точка X. Прямая, проходящая через точку X, пересекает окружность в точках Y и Z (см. рис. 7б). Тогда величина XY× XZ не зависит от выбора прямой (теорема о пересечении хорд окружности или теорема о произведении отрезка секущей и ее внешней части).

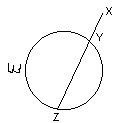
Эта величина называется степенью точки X относительно окружности w (если точка X лежит вне w , то произведение берется со знаком «+», а если X – внутри w , то со знаком «–»).

Пусть две окружности пересекаются в точках А и С (см. рис. 7в). Тогда прямая АС –

геометрическое место точек плоскости, для которых степени

относительно этих окружностей равны. (Такую прямую называют радикальной осью этих окружностей). Если три окружности пересекаются попарно, то радикальная ось первых двух окружностей пересекает радикальную ось второй и третьей окружности в точке, степень которой по отношению к первой и третьей окружностям одинакова. Следовательно, эти три прямые пересекаются в одной точке.

«Стереометрическое» доказательство. Пусть данные окружности – проекции трех сфер на плоскость a , содержащую их центры (см. рис. 7а). Тогда их общие хорды – проекции окружностей, являющихся попарным пересечением сфер, на эту плоскость. Рассмотрим две точки, общие для трех сфер, которые симметричны относительно плоскости a . Их общая проекция на эту плоскость – точка пересечения трех хорд, что и требовалось доказать.

Докажем теперь утверждение задачи. Пусть окружность w ₁ проходит через точки A и C, а окружность w ₂ проходит через точки B и D, EF – их общая хорда (см. рис. 7г). Построим окружность w , описанную около прямоугольника ABCD. Тогда АС – общая хорда окружностей w и w ₁, а BD – общая хорда окружностей w и w ₂. По доказанному, прямые АС, BD и EF пересекаются в одной точке. В данном случае АС и BD пересекаются в центре О данного прямоугольника, поэтому хорда EF проходит через эту точку, что и требовалось доказать.

5.3. Количество пользователей интернета росло в течение всего года. При этом на четыре разных квартала (в каком-то порядке) пришлись: наибольший абсолютный прирост, наименьший абсолютный прирост, наибольший относительный прирост и наименьший относительный прирост. (Абсолютный прирост – разность между новым и старым значением величины. Относительный прирост – это абсолютный прирост, делённый на старое значение.)

Известно, что наименьший относительный прирост был раньше, чем наибольший относительный. В каком квартале был наибольший абсолютный прирост?

Ответ: в четвертом квартале.

Докажем, что если количество пользователей растет и относительный прирост увеличивается, то увеличивается и абсолютный прирост. Пусть A и B – количество пользователей в какие-то моменты времени, причем A < B, а абсолютный прирост составляет x и y человек соответственно. Тогда относительный прирост равен соответственно и . Если , то Bx < Ay < By, следовательно, x < y.

Таким образом, наибольший относительный прирост не мог быть ПОЗЖЕ, чем наибольший абсолютный, и потому был не позже третьего квартала. Аналогично, наименьший относительный прирост не мог быть РАНЬШЕ, чем наименьший абсолютный, и потому был не раньше второго квартала. Так как по условию задачи, наименьший относительный прирост был раньше, чем наибольший относительный, то они были во втором и третьем квартале соответственно. Следовательно, наибольший абсолютный прирост был позже, то есть в четвёртом квартале.