Математическая регата 10 классов 23.04.2005

1.1. Найдите все целые решения неравенства: |x + 3y – 5,5| + |x – 3y| £ .

1.2. Противоположные стороны шестиугольника попарно равны и параллельны, кроме того, в него можно вписать окружность. Обязательно ли этот шестиугольник – правильный?

1.3. В некотором числе переставили цифры и получилось в три раза меньшее число. Докажите, что исходное число делилось на 27.

2.1. Найдите все значения параметра а, для которых система уравнений 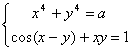имеет единственное решение.

2.2. В остроугольном треугольнике ABC проведены высоты AA₁ и CC₁. На высоте AA₁ выбрана такая точка D, что A₁D = C₁D. Точка E – середина стороны AC. Докажите, что точки A, C₁, D и E лежат на одной окружности.

2.3. Имеет ли уравнение 5x⁴ = 4y³ + 3 целочисленные решения?

3.1. Докажите, что если , то sinx + tg²x + sin³x + tg⁴x + ... < 1,2.

3.2. Внутри треугольника выбраны две точки. Расстояния от одной из них до сторон треугольника равны 1, 3 и 15, а от другой (стороны рассматриваются в том же порядке) – 4, 5 и 11. Найдите радиус окружности, вписанной в данный треугольник.

3.3. Пятизначное число назовем «неразложимым», если оно не раскладывается в произведение двух трехзначных чисел. Какое наибольшее количество таких чисел может идти подряд?

4.1. Докажите, что для любых значений x выполняется неравенство: .

4.2. Можно ли разрезать куб на три равные части, не являющиеся ни параллелепипедами, ни пирамидами?

4.3. На шахматной доске стоят черная и белая шашки. За один ход разрешается сдвинуть одну из них на соседнюю (по стороне) клетку. Существует ли такая последовательность ходов, при которой каждое возможное расположение шашек встречается ровно один раз?

5.1. Существует ли многочлен P(x) такой, что P(1) = 1, P(2) = 2, P(3) = 3, P(4) = 4, P(5) = 5, а его значения при всех остальных натуральных x – иррациональны?

5.2. В выпуклом четырехугольнике АВСD: BC = 4, Ð АDС = 60° , Ð BАD = 90° . . Найдите длину CD.

5.3. Каких треугольников с целыми сторонами больше: с периметром 2005 или с периметром 2008?