 .
.Задания | Результаты | Решения (doc-файл) | Решения (html-файл)
9 класс. Первый тур (10 минут; каждая задача – 6 баллов
1.1. Сократите дробь: 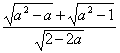 .
.
1.2. В прямоугольной трапеции АВСD высота АВ равна сумме оснований АD и ВС. Биссектриса угла АВС пересекает сторону СD в точке K. В каком отношении эта точка делит СD?
1.3. В какое наименьшее количество цветов надо раскрасить доску 100´ 100, чтобы никакие две соседние клетки (по горизонтали, вертикали или диагонали) не были окрашены в одинаковый цвет?
Второй тур (15 минут; каждая задача – 7 баллов
).2.1.
Известно, что каждое из уравнений x2 + 2bx + c = 0 и x2 + 2cx + b = 0, где b > 0 и с > 0, имеет хотя бы один корень. Произведение всех корней этих уравнений равно 1. Найдите b и c.2.2. Существуют ли четыре отрезка с длинами a, b, c и d такие, что можно составить две трапеции: одну с основаниями а и b и боковыми сторонами c и d, а другую – с основаниями c и d и боковыми сторонами а и b?
2.3. Существует ли натуральное n такое, что число n2004 – 1 является какой-либо степенью двойки?
Третий тур (15 минут; каждая задача – 7 баллов
).3.1.
Пусть xyz = 1 и3.2. В треугольнике АВС точка М – середина АС, МD и МЕ – биссектрисы треугольников АВМ и СВМ соответственно. Отрезки ВМ и DE пересекаются в точке F. Найдите MF, если DE = d.
3.3. На прямой сначала отметили 100 точек, затем отметили середины всех отрезков с концами в ранее отмеченных точках. Какое наименьшее количество точек могло получиться в итоге?
Четвертый тур (20 минут; каждая задача – 8 баллов
).4.1.
Докажите, что4.2.
Существует ли треугольник, в котором радиус описанной окружности равен радиусу вневписанной окружности (то есть, окружности, касающейся одной из его сторон и продолжений двух других)?4.3.
Некоторое простое число возвели в четвертую степень и получили десятизначное число. Могут ли все цифры полученного числа быть различными?
Пятый тур (25 минут; каждая задача – 9 баллов
).5.1.
Существуют ли числа a, b, c и d, удовлетворяющие неравенству 0 < a < b < c < d, такие что уравнения x4 + bx + c = 0 и x4 + ax + d = 0 имеют хотя бы один общий корень?5.2.
Дан квадрат АВСD. Луч АЕ пересекает сторону ВС, причем Ð ВАЕ = 30° , а Ð ВСЕ = 75° . Найдите Ð CBЕ.5.3.
На окружности расположены шестнадцать точек. Эти точки требуется соединить восемью хордами, не имеющими общих точек (даже общих концов). Сколькими способами это можно сделать?| 1 тур | 2 тур | 3 тур | 4 тур | 5 тур | Сумма | |||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||
| 2 А | 0 | 0 | 6 | 0 | 0 | 0 | 7 | 7 | 3 | 0 | 0 | 8 | 0 | 0 | 0 | 31 |
| 2 Б | 3 | 6 | 6 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 25 |
| 2 В | 6 | 2 | 0 | 0 | 0 | 7 | 7 | 1 | 3 | 8 | 1 | 8 | 0 | 0 | 0 | 43 |
| 82 Черноголовка | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 7 | 6 | 0 | 0 | 8 | 9 | 0 | 0 | 36 |
| Переславль | 0 | 0 | 6 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 17 |
| 2 Е | 0 | 6 | 6 | 0 | 0 | 6 | 0 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 26 |
| 2 Ж | 3 | 0 | 6 | 7 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 8 | 9 | 0 | 0 | 39 |
| 2 И | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 5 | 1 | 0 | 0 | 7 |
| 1576 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 8 | 1 | 0 | 0 | 10 |
| 2 Л | 3 | 6 | 6 | 7 | 0 | 7 | 1 | 1 | 0 | 0 | 1 | 8 | 0 | 0 | 2 | 42 |
| 2 М | 6 | 6 | 6 | 7 | 0 | 7 | 7 | 7 | 7 | 8 | 0 | 8 | 8 | 9 | 0 | 86 |
| 2 Н | 0 | 6 | 6 | 1 | 0 | 7 | 7 | 7 | 7 | 0 | 2 | 8 | 0 | 0 | 0 | 51 |
| 5 А Долгопрудный | 0 | 6 | 6 | 6 | 0 | 7 | 1 | 7 | 7 | 0 | 2 | 8 | 0 | 0 | 3 | 53 |
| 5 Б Долгопрудный | 0 | 0 | 0 | 7 | 0 | 7 | 7 | 7 | 7 | 8 | 0 | 8 | 9 | 7 | 0 | 67 |
| 7 А | 6 | 3 | 0 | 0 | 0 | 0 | 0 | 7 | 6 | 0 | 0 | 0 | 9 | 0 | 0 | 31 |
| 7 Б | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 5 | 0 | 0 | 12 | |
| 11 А Долгопружный | 0 | 0 | 6 | 1 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 |
| 11 Б Долгопрудный | 0 | 0 | 1 | 1 | 1 | 0 | 7 | 1 | 2 | 0 | 0 | 0 | 0 | 1 | 0 | 14 |
| 17 | 0 | 0 | 6 | 1 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 1 | 0 | 0 | 13 |
| 57 | 0 | 6 | 6 | 7 | 0 | 7 | 7 | 7 | 6 | 0 | 0 | 8 | 0 | 0 | 0 | 54 |
| 91 А | 0 | 1 | 0 | 0 | 0 | 2 | 1 | 4 | 6 | 0 | 0 | 8 | 9 | 1 | 0 | 32 |
| 91 Б | 0 | 0 | 6 | 7 | 0 | 0 | 7 | 0 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 24 |
| Интеллектуал А | 6 | 4 | 6 | 1 | 7 | 6 | 7 | 4 | 6 | 0 | 2 | 0 | 0 | 0 | 0 | 49 |
| Интеллектуал Б | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 2 | 7 | 0 | 0 | 7 | 9 | 0 | 0 | 32 |
| 174 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| 218 А | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 7 | 7 | 0 | 0 | 8 | 9 | 9 | 0 | 46 |
| 218 Б | 0 | 0 | 6 | 7 | 2 | 0 | 1 | 1 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 21 |
| 1018 А | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1018 Б | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 0 | 3 | 0 | 1 | 0 | 16 |
| 1101 А | 0 | 4 | 1 | 0 | 0 | 0 | 7 | 0 | 6 | 0 | 0 | 0 | 0 | 1 | 0 | 19 |
| 1101 Б | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 1 | 6 | 0 | 0 | 0 | 9 | 1 | 0 | 24 |
| 1189 А | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 8 | 9 | 0 | 0 | 27 |
| 1189 Б | 6 | 2 | 6 | 0 | 0 | 7 | 7 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 35 |
| 1189 В | 0 | 6 | 0 | 0 | 0 | 7 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | |
| 1511 А | 0 | 0 | 6 | 0 | 0 | -1 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 8 | |
| 1511 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 8 |
| 1514 А | 6 | 6 | 6 | 7 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 32 |
| 1514 Б | 0 | 2 | 6 | 7 | 0 | 7 | 0 | 0 | 7 | 8 | 0 | 8 | 0 | 1 | 0 | 46 |
| 1514 В | 0 | 6 | 2 | 7 | 0 | 0 | 7 | 7 | 7 | 7 | 0 | 8 | 0 | 0 | 0 | 51 |
| 1523 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 1537 А | 6 | 0 | 2 | 7 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 8 | 9 | 0 | 0 | 35 |
| 1537 Б | 6 | 0 | -1 | 7 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 |
| 1537 В | 4 | 6 | 2 | 7 | 0 | 0 | 0 | 7 | 6 | 0 | 0 | 0 | 9 | 1 | 0 | 42 |
| 1538 А | 0 | 0 | 1 | 5 | 0 | -1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 6 |
| 1538 Б | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1543 А | 0 | 6 | 6 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 21 |
| 1543 Б | 6 | 6 | 6 | 7 | 0 | 7 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 0 | 7 | 93 |
| 1543 В | 0 | 6 | 6 | 1 | 7 | 0 | 0 | 5 | 7 | 0 | 0 | 8 | 1 | 0 | 2 | 43 |
| 1543 Г | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 7 | 6 | 0 | 0 | 8 | 9 | 0 | 7 | 76 |
| 1543 Д | 0 | 0 | 0 | 1 | 0 | 0 | 7 | 7 | 6 | 0 | 0 | 8 | 4 | 0 | 4 | 37 |
| Фрязино А | 0 | 0 | 6 | 0 | 0 | 1 | 0 | 1 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 16 |
| 1741 А | 0 | 6 | 3 | 0 | 0 | 0 | 0 | 3 | 7 | 0 | 0 | 8 | 9 | 2 | 0 | 38 |
| 1741 Б | 0 | 0 | 2 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 9 |
| Фрязино Б | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| 2007 А | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 8 | 0 | 0 | 0 | 12 |
| 2007 Б | 6 | 0 | 0 | 7 | 0 | -1 | 7 | 2 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 25 |
| 2007 В | 0 | 0 | 2 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 2 |
| 2007 Г | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Кострома | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 1 | 0 | 0 | 0 | 4 |