Математическая регата 10 классов 22.05.2005

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Известно, что уравнение ax⁵ + bx⁴ + c = 0 имеет ровно три действительных корня. Сколько корней может иметь уравнение cx⁵ + bx + a = 0?

1.2. Существует ли замкнутая шестизвенная не плоская ломаная такая, что длины всех ее звеньев равны и углы между соседними звеньями равны?

1.3. Можно ли раскрасить в три цвета все ребра 99-угольной призмы так, что в каждой вершине сходятся все три цвета и у каждой грани (в том числе, у оснований) есть ребра всех трех цветов?

2.1. Решите систему уравнений: .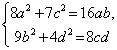

2.2. В параллелограмме АВСD точки Е и F – середины сторон ВС и CD соответственно. Могут ли лучи АЕ и AF делить угол ВАD на три равные части?

2.3. Натуральное число называется упрощенным, если оно является произведением ровно двух простых чисел (не обязательно различных). Какое наибольшее количество последовательных натуральных чисел может оказаться упрощенными?

3.1. Докажите неравенство: .

3.2. На отрезке АВ построена полуокружность, как на диаметре. На этой полуокружности выбраны произвольным образом точки P и Q. Точка С – пересечение прямых AP и BQ, а точка Х – пересечение касательных к полуокружности в точках Р и Q. Докажите, что прямые СХ и АВ перпендикулярны.

3.3. Таблица 5´ 5 заполнена числами 1, 2, ..., 25, причем любые два последовательных числа записаны в соседних (имеющих общую сторону) клетках. Какое наибольшее количество простых чисел может оказаться в одном столбце?

4.1. Существует ли треугольник, в котором синус одного угла равен косинусу другого и равен тангенсу третьего?

4.2. Во вписанном четырехугольнике длины двух противолежащих сторон равны а и b, острый угол между диагоналями равен j . Найдите все возможные значения радиуса окружности, описанной около четырехугольника.

4.3. Может ли функция, непрерывная на множестве действительных чисел, принимать во всех рациональных точках иррациональные значения, а во всех иррациональных точках – рациональные?

Пятый тур (15 минут; каждая задача – 7 баллов).

5.1. Найдите наибольшее и наименьшее значение выражения x² + xy + y², если 1 £ x² + y² £ 2.

5.2. Во вписанном четырехугольнике АВСD точка М лежит на стороне AD, причем BM || CD и CM || BA. Найдите ВС, если АМ = а; DM = b.

5.3. На плоскости отмечены вершины равностороннего треугольника. На каждом шаге разрешается отметить середину отрезка, если его концы также отмечены. Может ли на каком-то шаге оказаться отмеченным центр исходного треугольника?