11 класс
Первый тур (10 минут; каждая задача – 6 баллов
).1.1.
Петя записал на доске величины двух углов a и b . Верно ли, что, независимо от значений a и b , Вася сможет поставить перед одним из углов знак синуса, а перед другим – знак косинуса так, чтобы сумма синуса одного угла и косинуса другого была не больше, чемОтвет
: да, верно.Пусть это не так, то есть sina
+ cosb
> ![]() и cosa
+ sinb
>
и cosa
+ sinb
> ![]() . Тогда существуют различные способы прийти к противоречию.
. Тогда существуют различные способы прийти к противоречию.
Первый способ. Сложим эти неравенства почленно: (sina
+ cosa
) + (sinb
+ cosb
) > 2![]() Û
Û
![]() sin(a
+ 45°
) +
sin(a
+ 45°
) + ![]() sin(b
+ 45°
) > 2
sin(b
+ 45°
) > 2![]() Û
sin(a
+ 45°
) + sin(b
+ 45°
) > 2, что невозможно.
Û
sin(a
+ 45°
) + sin(b
+ 45°
) > 2, что невозможно.
Второй способ. Так как эти неравенства содержат только положительные члены, то перемножим их: sina cosa + sinb cosb + (sina sinb + cosa cosb ) > 2 Û 0,5sin2a + 0,5 sin2b + cos(a – b ) > 2, что невозможно.
1.2.
Площади боковых граней треугольной призмы относятся как 5 : 4 : 2. Найдите наибольший из углов между этими гранями.Ответ:
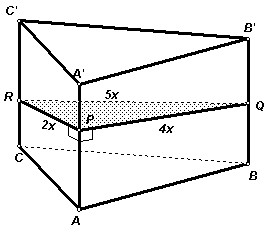
Рассмотрим призму АВС
A’B’C’ и ее перпендикулярное сечение PQR (см. рис. 1). Так как площадь боковой грани равна произведению бокового ребра призмы и стороны проведенного сечения, то стороны треугольника PQR пропорциональны площадям боковых граней, то есть равны 5x, 4x и 2x.Углы этого треугольника являются линейными углами двугранных углов между боковыми гранями. Наибольшим из них является угол, лежащий против наибольшей стороны треугольника.
По теореме косинусов
|
1 |
2 |
1 |
2 |
1 |
|
3 |
4 |
3 |
4 |
3 |
|
1 |
2 |
1 |
2 |
1 |
|
3 |
4 |
3 |
4 |
3 |
|
1 |
2 |
1 |
2 |
1 |
1.3.
Каждая из клеток квадрата 5´ 5 покрашена в один из четырех цветов так, что в каждом квадрате 2´ 2 присутствуют все четыре цвета. Какое наибольшее количество клеток одного цвета может быть в данном квадрате?Ответ
: 9.Пример приведен на рис. 2а (клетки с цифрой 1).
Докажем, что больше девяти клеток одного цвета быть не может.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Две клетки, имеющие общую сторону или общую вершину, не могут иметь одинаковый цвет – иначе найдется квадрат с двумя клетками одного цвета. Разобьем данный квадрат на четыре угловых квадрата и «крест» (см. рис. 2б). В каждом угловом квадрате может быть не более одной клетки каждого цвета, итого не более четырех. Внутри «креста» клетки одного цвета не должны граничить, поэтому их не больше пяти.
Второй тур (15 минут; каждая задача – 7 баллов
).
2.1.
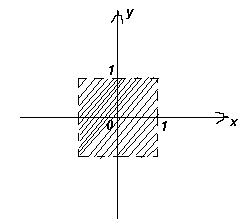
Укажите множество точек (x; y) координатной плоскости, удовлетворяющих неравенству:Ответ
: см. рис. 3.Пусть а = 1 – x2; b = 1 – y2, тогда данное неравенство примет вид: ![]() . Это неравенство равносильно системе:
. Это неравенство равносильно системе: ![]() Û
Û
![]() Û
Û
![]() . Таким образом, искомое множество точек удовлетворяет системе:
. Таким образом, искомое множество точек удовлетворяет системе: 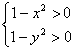 Û
Û
![]() . Оно состоит из внутренних точек квадрата с вершинами: (1; 1), (1; –1), (–1; –1) и (–1; 1).
. Оно состоит из внутренних точек квадрата с вершинами: (1; 1), (1; –1), (–1; –1) и (–1; 1).
2.2.
В остроугольном треугольнике АВС из основания высоты опущены перпендикуляры DM и DN на стороны АВ и ВС. Найдите угол АВС, если MN = m; BD = h.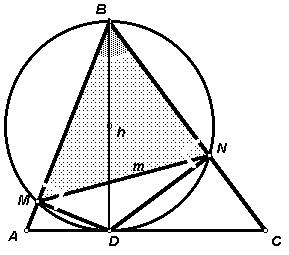
Ответ
: arcsinТак как треугольники
BMD и BND – прямоугольные, то около четырехугольника MBND можно описать окружность с диаметром BD (см. рис. 4). Рассмотрим треугольник MBN, вписанный в эту окружность. По следствию из теоремы синусов:2.3. Найдите наибольший общий делитель всех чисел, имеющих вид: 11n – 6n – 5n, где n – натуральное число, отличное от 1.
Ответ: 30.
При любых натуральных
n получим, что (11n – 6n) M (11 – 6) и (11n – 5n) M (11 – 5), следовательно, каждое число указанного вида кратно 5 и кратно 6, то есть кратно 30.При
n = 2 11n – 6n – 5n = 112 – 62 – 52 = 60. Значит, искомый НОД равен либо 30, либо 60. При n = 3 значение данного выражения равно 990, а это число не делится на 60.Первую часть доказательства можно провести иначе. При любых натуральных
n получим, что 11n º 1 (mod 5) и 6n º 1 (mod 5), следовательно, 11n – 6n – 5n делится на 5. Кроме того, при любых натуральных k получим, что 112k + 1 º –1 (mod 6) и 52k + 1 º –1(mod 6), то есть 112k + 1 – 52k + 1 кратно 6. Аналогично, 112k º 1 (mod 6), 52k º 1 (mod 6), то есть 112k – 52k кратно 6. Тем самым 11n – 6n – 5n делится на 30 при любом натуральном n.
Третий тур (20 минут; каждая задача – 8 баллов
).3.1.
Известно, что для двух острых углов треугольника выполняется равенство:Ответ
: 90° .Преобразуем:
Пусть
sina – cosb > 0, то есть sina > cosb = sin(90° – b ). Так как 0 < 90° – b < 90° , то a > 90° – b , поэтому cosa < cos(90° – b ) = sinb , то есть cosa – sinb < 0 и полученное равенство выполняться не может. Аналогичное противоречие получится, если предположить, что sina – cosb < 0. Следовательно sina – cosb = sinb – cosa = 0, то есть a + b = 90° .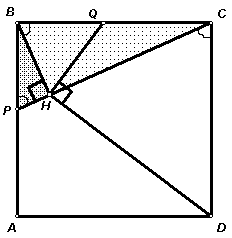
3.2.
Точки P и Q лежат на сторонах квадрата АВСD, причем BP = BQ. Точка H – основание перпендикуляра, опущенного из вершины В на РС. Докажите, что угол DHQ – прямой.Первый способ. Так как
BH – высота, проведенная к гипотенузе прямоугольного треугольника РВС (см. рис. 5а), то треугольники РВН и ВСН подобны с коэффициентом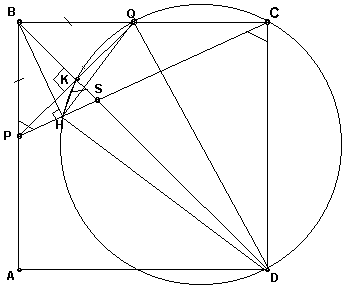
Рассмотрим поворотную гомотетию
Второй способ
. Рассмотрим треугольники BQH и CDH (см. рис. 5а): Ð QBH = Ð BPC = Ð DCH;Третий способ
. Пусть отрезки BD и PQ пересекаются в точке К (см. рис. 5б). Так как BP = BQ, то Ð QKD = 90° = Ð QCD. Следовательно, точки C и K лежат на окружности с диаметром QD. Докажем, что точка H лежит на той же окружности. Пусть BD и CP пересекаются в точке S. Тогда в треугольнике BSP отрезки PK и BH являются высотами, следовательно Ð SKH = Ð BPH. Так как Ð BPH = Ð DCH, то Ð DKH = Ð DCH. Это и означает, что H лежит на окружности с диаметром QD, то есть Ð DHQ = 90° .3.3. В футбольном турнире каждая команда сыграла с каждой по одному разу. Ровно треть команд хотя бы раз сыграли вничью, а ровно 75% остальных команд не обошлись без поражений. Сколько результативных матчей было сыграно в турнире?
Ответ: 14.
Без ничьих провели турнир ![]() команд, то есть эти команды имели только победы или поражения. Из условия задачи следует, что поражения имели 75% от этих двух третей, то есть ровно половина участвующих команд. Команды, не имевшие ничьих и поражений, только побеждали. Их количество составляет 1 –
команд, то есть эти команды имели только победы или поражения. Из условия задачи следует, что поражения имели 75% от этих двух третей, то есть ровно половина участвующих команд. Команды, не имевшие ничьих и поражений, только побеждали. Их количество составляет 1 – ![]() –
– ![]() =
= ![]() от общего количества команд, при этом в турнире может быть только одна такая команда. Значит, в этом турнире участвовало 6 команд.
от общего количества команд, при этом в турнире может быть только одна такая команда. Значит, в этом турнире участвовало 6 команд.
Поэтому ничейные результаты имели ровно две команды, а это возможно только в случае, если вничью они сыграли между собой. Следовательно, все матчи турнира, кроме одного, были результативными. Поскольку в турнире из шести команд проводится ![]() = 15 встреч, то результативных матчей было 14.
= 15 встреч, то результативных матчей было 14.
Четвертый тур (25 минут; каждая задача – 9 баллов
).4.1.
При каких значениях а неравенствоОтвет
: при aÎ (–¥ ; –4) | aÏ Z, или a = –4 или aÎ [4; 5).![]() Û
Û
![]() Û
Û
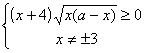 Û
Û
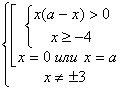 .
.
Решение первого неравенства полученной системы зависит от знака числа а, поэтому рассмотрим три случая:
1)
а = 0. Тогда неравенство x(a – x) > 0 не имеет решений, а система имеет единственное решение: х = 0.2)
а > 0. Тогда решением неравенства x(a – x) > 0 является (0; а), кроме того, решением системы являются х = 0 или х = а. Так как [0; а]Ì [–4; +¥ ), то, учитывая, что х ¹ ± 3, получим, что четырьмя целыми решениями системы должны являться числа 0, 1, 2 и 4, что возможно, если а ³ 4. Для того, чтобы система не имела других целых решений, должно выполняться условие а < 5. Таким образом, в этом случае получим: 4 £ а < 5.3)
а < 0. Тогда решением неравенства x(a – x) > 0 является (а; 0), кроме того, решением системы являются х = 0 или х = а.А) Если а
> –4, то, учитывая, что х ¹ ± 3, в [a; 0] могут попасть только –2; –1 и 0, то есть не более трех целых чисел.Б) Если
a £ –4, то решением системы является [–4; –3) U (–3; 0] U {a}. Это множество содержит ровно четыре целых числа, а именно, –4; –2; –1 и 0, т. и т. т., когда а = –4 или а < –4, но не является целым.Возможны также другие способы решения, использующие, например, метод интервалов или систему координат (
x, a).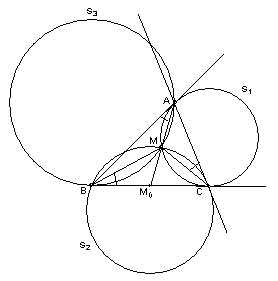
4.2.
Окружность S1 касается сторон угла АВС в точках А и С. Окружность S2 касается прямой АС в точке С и проходит через точку В. М – вторая точка пересечения окружностей S1 и S2. В каком отношении прямая АМ делит отрезок ВС?Ответ
: 1 : 1.Первый способ
. Сделаем дополнительное построение: через точки A, M и B проведем окружность S3 (см. рис. 6а). Так как окружность S1 касается прямой АВ в точке А, то Ð MAB = Ð MCA. Так как окружность S2 касается прямой АС в точке С, то Ð MBС = Ð MCA. Следовательно, Ð MAB = Ð MВC, поэтому прямая ВС – касательная к окружности S3.Таким образом, ВС – общая касательная к окружностям
S1 и S3, а прямая АМ – их общая секущая. Пусть M0 – точка пересечения прямой АМ и отрезка ВС. Тогда, по свойству секущей к окружности, M0B2 = M0A× M0M = M0C2, то есть M0B = M0С.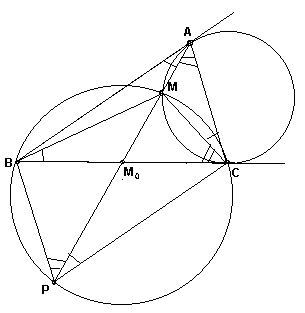
Второй способ
. Пусть прямая AM пересекается с отрезком BC в точке M0, а окружность S2 эта же прямая вторично пересекает в точке P (см. рис. 6б). Тогда, используя свойство углов между касательной и хордой и свойство вписанных углов, опирающихся на одну дугу, получим, что Ð BAP = Ð ACM = Ð MBC = Ð MPC и Ð MAC = Ð BCM = Ð BPM. Следовательно, четырехугольник ABPC – параллелограмм, значит BM0 = CM0.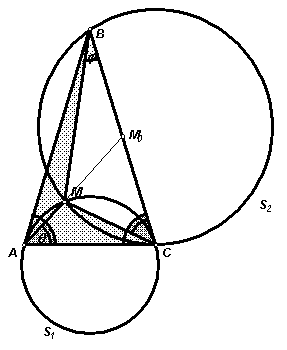
Третий способ
. Пусть Ð MBC = j ; Ð MCB = q (см. рис. 6в). Тогда, используя свойство углов между касательной и хордой и свойство вписанных углов, опирающихся на одну дугу, получим: j = Ð MBC = Ð MCА = Ð MАB; q = Ð MCB = Ð MАC. Следовательно, треугольники МАС и МСВ подобны (по двум углам), поэтомуДокажем
теперь, что треугольники АМС и АМВ равновелики. Действительно, SD AMC =Из полученного равенства площадей следует, что точка М лежит на медиане АМ
0 треугольника АВС, то есть прямая АМ делит отрезок ВС пополам.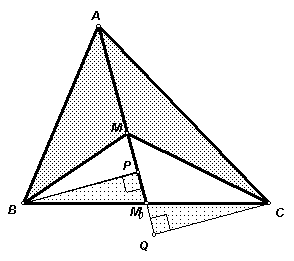
Действительно, из полученного равенства площадей следует равенство перпендикуляров
CQ и BP, опущенных из вершин треугольника на прямую АМ (см. рис. 6г), из которого, в свою очередь, следует равенство прямоугольных треугольников CQM0 и BPM0 (по катету и острому углу), а значит и равенство отрезков CM0 и BM0.
4.3.
Найдите два различных натуральных числа, сумма квадратов которых является кубом, а сумма кубов – квадратом.Ответ: например, 625 и 1250.
Рассмотрим два числа, сумма кубов которых является квадратом, например, 1 и 2. Действительно, 1
3 + 23 = 9 = 32. Если каждое из этих чисел умножить на квадрат произвольного натурального числа k, то сумма кубов полученных чисел по-прежнему будет квадратом:Отметим, что условию
задачи удовлетворяет любая пара чисел вида (625m6; 2× 625m6), где mÎ N.
Пятый тур (15 минут; каждая задача – 7 баллов
).5.1.
При каких значениях параметра а уравнениеОтвет
: ни при каких.Рассмотрим функцию f(x) = ![]() . Так как |sinxcosx| = |0,5sin2x| £
0,5, то D(f) = R. Кроме того, f(–x) =
. Так как |sinxcosx| = |0,5sin2x| £
0,5, то D(f) = R. Кроме того, f(–x) = ![]() =
= ![]() =
= ![]() = –
= –![]() = – f(x), то есть f(x) – нечетная функция. Функция g(x) = ax – также нечетная. Следовательно, если точка (x0; y0) является точкой пересечения графиков y = f(x) и y = g(x), то и точка (–x0; –y0) является их точкой пересечения. Так как f(0) = g(0) = 0, то среди этих точек есть начало координат. Таким образом, количество общих точек этих графиков не может быть четным, то есть данное уравнение не может иметь ровно 2006 корней.
= – f(x), то есть f(x) – нечетная функция. Функция g(x) = ax – также нечетная. Следовательно, если точка (x0; y0) является точкой пересечения графиков y = f(x) и y = g(x), то и точка (–x0; –y0) является их точкой пересечения. Так как f(0) = g(0) = 0, то среди этих точек есть начало координат. Таким образом, количество общих точек этих графиков не может быть четным, то есть данное уравнение не может иметь ровно 2006 корней.
Заметим, что утверждение: «данное уравнение имеет нечетное количество корней» является неверным, так как при а = 0 уравнение имеет бесконечное множество корней.
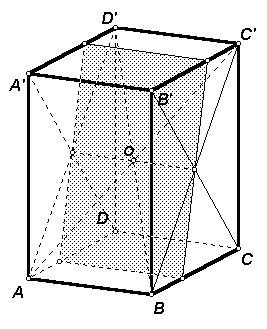
5.2. Внутри куска сыра, имеющего форму прямоугольного параллелепипеда, есть одна дырка шарообразной формы. Можно ли провести плоский разрез, параллельно одному из ребер, чтобы сыр разрезался на два куска одинакового объема? (Предполагается, что «местонахождение» дырки нам известно.)
Ответ: да, можно.
Любой параллелепипед имеет центр симметрии – точку О, в которой пересекаются его диагонали (см. рис. 7). Любая плоскость, проходящая через центр симметрии, делит параллелепипед на две равные части. Кроме того, любая плоскость, проходящая через центр шара, делит его на две равные части.
Проведем через точку О прямую, параллельную какому-нибудь ребру параллелепипеда, например, ребру АВ (см. рис. 7). Искомый разрез есть сечение параллелепипеда плоскостью, проходящей через эту прямую и центр шара (дырки). Построенное сечение параллельно ребру АВ по признаку параллельности прямой и плоскости.
5.3.
Все натуральные числа раскрашены в два цвета: синий и красный так, что чисел каждого цвета бесконечно много. Докажите, что найдется число, которое является одновременно суммой двух синих чисел и суммой двух красных чисел.Возможны два случая. 1) Начиная с какого-то места, цвета соседних чисел всегда различны, то есть, начиная с этого места, четные числа имеют один цвет, а нечетные – другой. Тогда любое четное число, начиная с некоторого, можно представить как сумму двух различных четных чисел и как сумму двух различных нечетных чисел.
2) Имеется бесконечное множество одноцветных отрезков, имеющих длину больше единицы. Выберем любой из них, кроме самого первого. Такой отрезок начинается с числа
n > 1 и заканчивается числом m. Тогда число n + m, являющееся суммой двух чисел одного цвета, можно также представить и как сумму двух чисел другого цвета: n + m = (n – 1) + (m + 1).