1.1. (6 баллов) Вычислите: 2007Ч 200820082008 – 2008Ч 200720072007.

Ответ: 0.

Преобразуем, разложив двенадцатизначные числа на два множителя: 2007Ч 200820082008 – 2008Ч 200720072007 = 2007Ч 2008Ч 100010001 – 2008Ч 2007Ч 100010001 = 0.

1.2. (6 баллов) Какое наибольшее количество лучей на плоскости может выходить из одной точки, чтобы каждый угол, образованный двумя соседними лучами, был тупым? (Дайте ответ и объясните, почему больше лучей выходить не может.)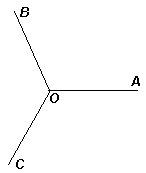

Ответ: три.

Три луча можно расположить требуемым образом, например, если углы между соседними лучами с началом в точке О равны по 120° (см. рис. 1).

Предположим, что можно расположить указанным образом более трех лучей. Тогда сумма величин всех тупых углов, образованных соседними лучами, будет больше, чем 90° Ч 4 = 360° , что невозможно.

1.3. (6 баллов) Коля написал на карточках натуральные числа 1, 10, 10², ..., 10¹⁰⁰. Затем часть карточек он положил в правый карман, часть -- в левый, а остальные выбросил (но не все). Может ли сумма чисел в правом кармане оказаться равной сумме чисел в левом кармане? Объясните ответ.

Сумма любого количества чисел, записанных на карточках, является числом, десятичная запись которого состоит только из единиц и нулей. При этом единицы будут стоять на тех же позициях, что и в слагаемых. Так как каждое из данных чисел является слагаемым только в одной из сумм, то единицы в этих суммах будут стоять в различных разрядах. Поэтому, независимо от того, как разложены карточки по карманам, суммы чисел в левом и правом карманах не могут быть равными.

2.1. (7 баллов) Гвоздь, три винта и два шурупа вместе весят 24 грамма; два гвоздя, четыре шурупа и пять винтов вместе весят 44 грамма. Сколько весят вместе три гвоздя, четыре винта и шесть шурупов?

Пусть гвоздь весит Г граммов, винт весит В граммов, а шуруп – Ш граммов. Тогда условие задачи можно записать в виде двух равенств: Г + 3В + 2Ш = 24 (1) и 2Г + 4Ш + 5В = 44 (2). Сложив равенства (1) и (2), получим, что 3Г + 8В + 6Ш = 68 (3).

Теперь для ответа на вопрос задачи останется выяснить, сколько весит винт. Для этого умножим на 2 равенство (1) и из полученного равенства вычтем равенство (2). Получим: (2Г + 6В + 4Ш) – (2Г + 4Ш + 5В) = 48 – 44, то есть В = 4. Следовательно, 3Г + 4В + 6Ш = 68 – 16 = 52.

2.2. (7 баллов) Три наследника разделили квадратный садовый участок со стороной 60 метров на три прямоугольные части равной площади. При этом каждые два наследника стали соседями. Какова общая длина забора, построенного внутри участка для отделения трех частей друг от друга?

Ответ: 100 метров.

Рассмотрим возможные способы разбиения квадрата на три прямоугольника. Один прямоугольник «отрезается» прямой, параллельной стороне квадрата, после чего есть ровно два способа разбиения одного из получившихся прямоугольников на два (см. рис. 2а, б). Второй способ разбиения квадрата (см. рис. 2б) не удовлетворяет условию, так как в этом случае два участка не имеют общей границы.

Для разбиения, показанного на рис. 2а, найдем общую длину границы между участками. Площадь садового участка равна 60² = 3600 (м²), поэтому каждому наследнику достался прямоугольный участок площадью 1200 м². Ширина каждого из прямоугольников, расположенных на рис. 2а вертикально, равна половине стороны квадрата, то есть 30 м, поэтому их высота равна 1200 : 30 = 40 (м). Следовательно, длина внутреннего забора равна 40 + 60 = 100 (м).

2.3. (7 баллов) Известно, что

35! = 10333147966386144929а66651337523200000000. Восстановите цифру а и объясните. (Напомним, что n! = 1Ч 2Ч 3Ч ...Ч (n – 1) Ч n.)

Ответ: а = 6.

Заметим, что число 35! делится на 9, так как содержит множитель 9. Следовательно, сумма цифр записанного числа должна делиться на 9. Подсчитаем ее: 1 + 3 + 3 + 3 + 1 + 4 + 7 + 9 + 6 + 6 + 3 + 8 + 6 + 1 + 4 + 4 + 9 + 2 + 9 + а + 6 + 6 + 6 + 5 + 1 + 3 + 3 + 7 + 5 + 2 + 3 + 2 = 138 + а. Так как а – цифра, то 138 Ј 138 + а Ј 147. В этом промежутке есть ровно одно число, делящееся на 9. Этим числом является 144, то есть а = 6.

3.1. (7 баллов) Чайку кормят с плывущего катера. Вниз бросают кусок хлеба, чайка за 3 секунды поднимает кусок с поверхности моря, а затем за 12 секунд догоняет катер. Войдя в залив, катер уменьшил скорость в два раза. Какое время теперь потребуется чайке, чтобы догнать катер, после того как она поднимет кусок хлеба?

Первый способ. Из условия задачи следует, что одно и то же расстояние чайка пролетает за 12 секунд, а катер проходит за 12 + 3 = 15 секунд. Следовательно, отношение скорости чайки к скорости катера (до входа в залив) равно 15 : 12 = 5 : 4. После того, как катер войдет в залив, это отношение станет равным 5 : 2. Значит, чтобы теперь преодолеть одно и то же расстояние, чайке потребуется в 2,5 раза меньше времени, чем катеру. Так как разница во времени по-прежнему составляет три секунды, то из уравнения 2,5t – t = 3, где t – искомое время, находим, что t = 2.

Второй способ. Пусть скорость чайки равна x метров в секунду, а скорости катера равны 2y и y метров в секунду (до и после входа в залив соответственно). Тогда скорость сближения чайки и катера до входа в залив равна (x – 2y) м/с, а после входа в залив равна (x – y) м/с. В первом случае за 3 секунды катер успевает отплыть на расстояние 6y метров, а во втором случае – на расстояние 3y метров.

Пусть искомое время равно t секунд, тогда составляем систему уравнений: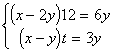 . Из первого уравнения получим, что x = 2,5y. Тогда из второго уравнения следует, что = 2.

3.2. (7 баллов) В остроугольном треугольнике АВС медиана АМ равна высоте BH, причем равны углы МАВ и НВА. Докажите, что треугольник АВС – равносторонний.

По условию, АВС – остроугольный треугольник, поэтому высота BH лежит внутри него (см. рис. 3).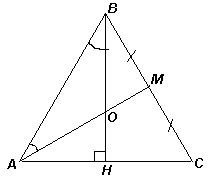

Первый способ. В треугольниках ABM и ABH: AB – общая сторона, АМ = BH и Р МАВ = Р НВА, поэтому D ABM = D BAH (по двум сторонам и углу между ними, см. рис. 3). Следовательно, Р АВM = Р ВAH и Р АMВ = Р ВHА = 90° .

Из первого равенства углов следует, что АС = ВС, а из второго равенства следует, что медиана АМ является также и высотой данного треугольника, поэтому АВ = АС.

Второй способ. Пусть О – точка пересечения отрезков АМ и BH (см. рис. 3). В треугольнике АОВ Р ОАВ = Р ОВА, следовательно ОА = ОВ. Тогда ОМ = АМ – ОА = ВН – ОВ = ОН.

В треугольниках АОН и ВОМ: ОА = ОВ, ОН = ОМ и Р НОА = Р МОВ, поэтому эти треугольники равны (по двум сторонам и углу между ними). Следовательно, Р АMВ = Р ВHА = 90° и Р MВО = Р HАО.

Из первого равенства следует, что медиана АМ треугольника АВС является его высотой, поэтому АВ = АС.

Из второго равенства следует, что Р MВА = Р AВО + Р MВО = Р ВAО + Р HAО = Р HAB, поэтому АС = ВС. Следовательно, треугольник АВС – равносторонний.

Школьники, уже знакомые с теоремой о сумме углов треугольника, могут использовать и другие способы доказательства. Например, доказав, что АВ = АС, можно получить, что Р САМ = Р ВАМ = Р НВА, а затем использовать, что сумма этих трех углов равна 90° . Тогда в равнобедренном треугольнике АВС Р САВ = 60° , откуда и следует, что треугольник АВС – равносторонний.

3.3. (7 баллов) В шахматном турнире играли пять человек. Каждый из них сыграл с каждым по одному разу. Победитель партии получал 1 очко, проигравший – 0 очков, а если партия заканчивалась вничью, то каждый получал по 0,5 очка. Известно, что половина партий турнира закончилась вничью, а игрок, занявший последнее место, проиграл все партии. Какое место занял игрок, набравший 3 очка?

4.1. (8 баллов) Числа а, b и с таковы, что выражения , и принимают одинаковое значение. Какое?

Первый способ. Пусть = x, тогда a + b = cx; b + c = ax; c +a = bx. Сложив полученные равенства почленно, получим: 2(a + b + c) = (a + b + c)x.

1) если a + b + c № 0, тогда x = 2;

2) если a + b + c = 0, тогда x = = –1.

Второй способ. Запишем цепочку равенств: Ы Ы . Последнее равенство выполняется, если или a + b + c = 0. Поочередно подставив полученные результаты в любое из данных выражений, получим, что искомое значение равно 2 или –1.

4.2. (8 баллов) Каждый из трех равных разносторонних треугольников разрезали по медиане, проводя эти медианы к различным сторонам. Всегда ли из получившихся шести треугольников можно составить (без «просветов» и «наложений») новый треугольник? Обоснуйте.

Ответ: да, всегда.

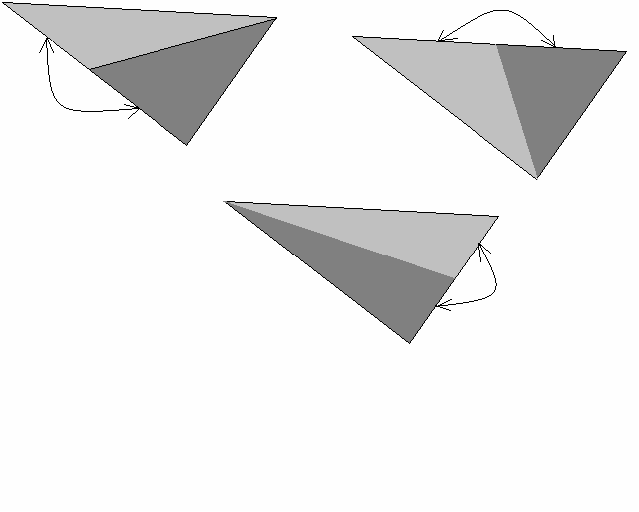
Разрезав треугольник по медиане, приложим два получившихся треугольника друг к другу, совместив две половинки разрезанной стороны (см. рис. 4а). В каждом случае мы получим новый треугольник, так как углы, образованные каждой медианой и стороной, к которой она проведена, в сумме составляют развернутый угол.

Полученные треугольники совместим равными сторонами так, чтобы вершины их углов, ранее составленные из двух частей, сошлись в одной точке (см. рис. 4б). Таким образом, в одной точке совместятся шесть углов, равных углам исходного треугольника, причем каждый угол встретится дважды. Следовательно, их сумма равна 360° , поэтому треугольники совместятся без «просветов» и «наложений» и образуют новый треугольник.

4.3. 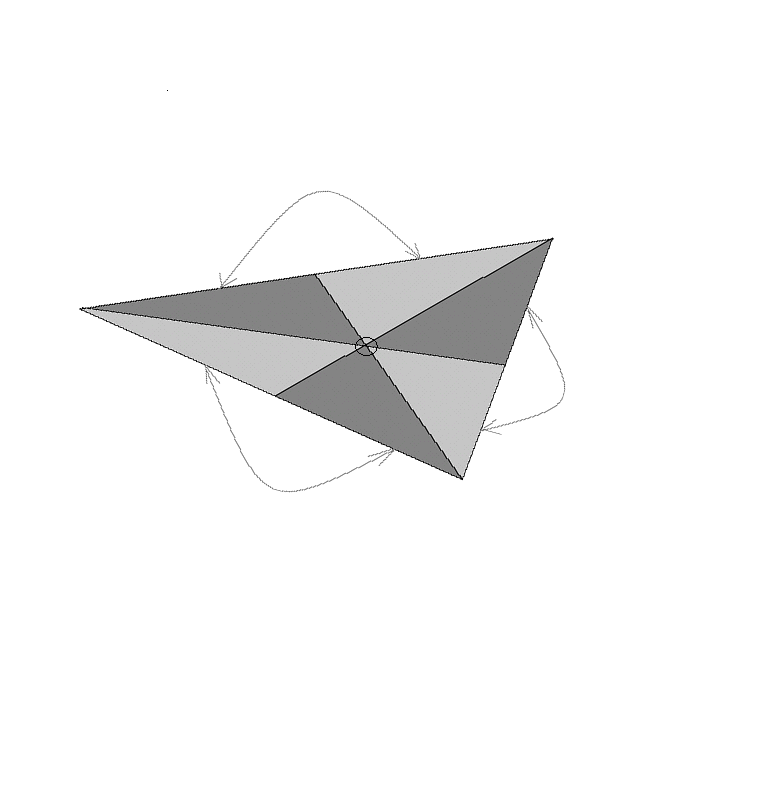(8 баллов) Сколькими способами можно заполнить таблицу 5ґ 5 клеток нулями и единицами так, чтобы сумма чисел в каждой строке и в каждом столбце была четной?

Ответ: количество способов равно 65536 = 2¹⁶.

Заметим также, что суммы чисел в прямоугольниках 4ґ 5 и 5ґ 4 должны оказаться четными. У этих прямоугольников есть общая часть – квадрат 4ґ 4 (см. рис. 5), поэтому четность суммы четырех чисел в последней строке и четность суммы четырех чисел в последнем столбце одна и та же. Следовательно, число, которое нужно поставить в последней угловой клетке, определяется однозначно.

Таким образом, мы можем любым способом расставить нули и единицы в квадрате 4ґ 4 и однозначно определить цифры в остальных клетках. Найдем, сколькими способами можно расставить нули и единицы в квадрате 4ґ 4. В каждую из 16 клеток можно поставить либо нуль, либо единицу независимо от других клеток. Поэтому количество искомых способов расстановки будет равно = 2¹⁶ = 65536.