8 класс
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Докажите, что для любых x и y выполняется неравенство: x2 – xy + y2 + x – y + 1 > xy.
Данное неравенство равносильно неравенству (
x – y)2 + (x – y) + 1 > 0. Пусть а = x – y, тогда это неравенство примет вид: a2 + a + 1 > 0. Справедливость такого неравенства можно доказать различными способами, например:1) a2 + a + 1 = a2 + a + ![]() +
+ ![]() = (a +
= (a + ![]() )2 +
)2 + ![]() > 0.
> 0.
2) Доказываемое неравенство равносильно неравенству 2
a2 + 2a + 2 > 0, которое выполняется, так как при любых значениях а имеем: 2a2 + 2a + 2 = (a2 + 2a + 1) + a2 + 1 = (а + 1)2 + a2 + 1 > 0.3) При любых значениях а выполняется неравенство
a2 і 0, поэтому при а > – 1 справедливость доказываемого неравенства следует из того, что a + 1 > 0. При а Ј –1 имеем: a2 + a + 1 = а(а + 1) + 1 > 0, так как числа а и а + 1 одного знака (или одно из них равно нулю).4) «Ветви» графика квадратичной функции f(a) = a2 + a + 1 направлены вверх, а дискриминант D = 1 – 4 < 0, поэтому при любых значениях а выполняется неравенство f(a) > 0.
Последний способ выходит за рамки программы 8 класса.

1.2.
Существует ли трапеция, в которой разность длин боковых сторон больше, чем разность длин оснований?Ответ: нет, не существует.
Пусть существует трапеция
ABCD, указанная в условии (см. рис. 1). Через вершину А меньшего основания проведем прямую, параллельную боковой стороне BC, которая пересечет основание CD в точке Q. Тогда ABCQ – параллелограмм (по определению). Следовательно, AQ = ВС и QC = AB, значит, DQ = DC – AB. Для треугольника AQD должно выполняться неравенство: AD + DQ > AQ Ы AD + DC – AB > BC Ы DC – AB > BC – AD. Последнее неравенство противоречит условию задачи, поэтому такой трапеции не существует.1.3.
Две команды разыграли первенство по десяти видам спорта. За победу в каждом из видов команда получала четыре очка, за ничью – два очка и за поражение – одно. Сумма очков, набранных обеими командами, оказалась равна 46. Сколько было ничьих?Ответ
: 4.Первый способ
. Если в каком-то из видов спорта команды сыграли вничью, то сумма очков, набранных ими за этот вид, равна 4, а при другом результате эта сумма равна 5, то есть в случае ничьей такая сумма на 1 меньше. Если бы ничьих не было вовсе, то сумма очков, набранных обеими командами, была бы равна 5Ч 10 = 50. В действительности же она на 4 очка меньше. Следовательно, было четыре ничьи.Второй способ. Пусть ничьих было
n, тогда результативных встреч было (10 – n). Из условия следует, что 4n + 5(10 – n) = 46 Ы n = 4.
Второй тур (15 минут; каждая задача – 7 баллов
).2.1.
С дробями разрешается делать две операции: 1) числитель увеличивать на 8, 2) знаменатель увеличивать на 7. Выполнив n указанных операций в произвольном порядке, из дробиОтвет: при
n = 113.Пусть первая операция выполнена
m раз, а вторая – k раз, причем m + k = n. Тогда выполняется равенство:Так как числа 64 и 49 – взаимно простые, то из полученного равенства следует, что
m кратно 49, то есть m і 49. Аналогично, k кратно 64, то есть k і 64. Таким образом, наименьшее значение n = 113 достигается, если m = 49, k = 64.2.2. В прямоугольном треугольнике центр вписанной окружности оказался равноудален от вершины прямого угла и середины гипотенузы. Найдите острые углы этого треугольника.
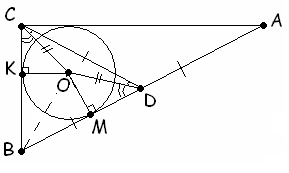
Ответ: 30° и 60° .
Пусть
D – середина гипотенузы AB прямоугольного треугольника ABC, О – центр окружности, вписанной в этот треугольник, K и M – точки касания этой окружности с меньшим катетом BC и гипотенузой AB соответственно (см. рис. 2).По свойству медианы прямоугольного треугольника, проведенной к гипотенузе,
CD =Первый способ. Из доказанного равенства треугольников следует, что
KC = MD. Кроме того, равны отрезки касательных к окружности BK и BM. Следовательно, BC = BK + KC = BM + MD = BD.Второй способ
. Из доказанного равенства треугольников следует, что Р KCO = Р MDО. Кроме того, треугольник COD – равнобедренный, значит Р OCD = Р ODC. Таким образом, Р BCD = Р BCO + Р OCD = Р BDO + Р ODC = Р BDC. Следовательно, BC = BD.Таким образом получим, что треугольник
BCD – равносторонний, то есть Р CBA = 60° , тогда Р CAB = 30° .Отметим, что при доказательстве равенства BC = BD можно обойтись и без равенства прямоугольных треугольников OKC и
OMD. А именно, можно сразу рассмотреть треугольники ВОС и BOD, в которых OС = OD, OB – общая сторона, и равны острые углы OВC и OBD, лежащие напротив равных сторон. Следовательно, углы ВCО и BDО либо равны, либо их сумма равна 180° (так называемый «четвертый признак равенства треугольников»). В рассматриваемой ситуации второй случай невозможен, так как оба угла – острые. Тогда D OВC = D OBD, следовательно, ВС = BD.Отметим также, что в приведенной конфигурации можно вычислить все углы, отмеченные на чертеже, так как треугольники OKC и OMD не только прямоугольные, но и равнобедренные. Поэтому
Р KCO = Р MDО = 45° , Р OCD = Р ODC = 15° .2.3.
В клетках таблицы 11´ 11 расставлены плюсы и минусы. Известно, что в каждой из 11 строк плюсов больше, чем минусов. Докажите, что хотя бы в двух столбцах плюсов также больше, чем минусов.Первый способ. По условию, в каждой строке больше плюсов, чем минусов. Значит, в каждой строке не менее, чем 6 плюсов, и общее количество плюсов не менее, чем 6×
11 = 66.Пусть не найдется двух столбцов, в которых плюсов больше, чем минусов, тогда найдутся 10 столбцов, в каждом из которых не больше, чем 5 плюсов. Значит, в этих столбцах не более, чем 5× 10 = 50 плюсов, поэтому в оставшемся столбце должно быть не менее, чем 66 – 50 = 16 плюсов. Но в столбце лишь 11 клеток – противоречие.
Второй способ. Пусть общее количество плюсов в таблице равно р, а общее количество минусов равно
m. Так как в каждой строке плюсов больше, чем минусов, то p – m ³ 11. Пусть не найдется двух столбцов, в которых плюсов больше, чем минусов, тогда m – p’ ³ 10, где p’ – количество плюсов в тех десяти столбцах, в которых плюсов меньше, чем минусов. Еще в одном столбце не может быть более 11 плюсов, поэтому p’ + 11 ³ p.Сложим почленно три записанных неравенства, тогда
p + 11 ³ p + 21 – противоречие.
Третий тур (20 минут; каждая задача – 8 баллов
).3.1.
В кинофильме «Самогонщики» три друга гонят самогон. У Труса течёт жидкость крепостью a% и стандартная бутыль наполняется за а часов, у Балбеса течёт жидкость крепостью b% и такая же бутыль наполняется за b часов, а у Бывалого – с% и за с часов соответственно. Для ускорения процесса друзья направили трубки аппаратов в одну бутыль и наполнили её за сутки. Найдите крепость получившейся смеси. (Крепость жидкости – это процент содержания в ней спирта).Ответ
: 72%.Первый способ
(«арифметический»). Представим себе, что из трубок течет чистый спирт, а дополнение его водой происходит отдельно. Из условия задачи следует, что каждый из самогонных аппаратов Труса, Балбеса и Бывалого закачивает за 1 час количество спирта, позволяющее повысить его итоговое содержание на 1%. Таким образом, крепость получающейся смеси растет на 3% в час, поэтому за 24 часа (после добавления воды) получится жидкость, крепостью 72%.Второй способ («алгебраический»). Самогонный аппарат Труса наполняет за час ![]() часть бутыли, Балбеса -
часть бутыли, Балбеса -
![]() часть бутыли, а Бывалого -
часть бутыли, а Бывалого -
![]() часть бутыли. Поскольку вся бутыль наполнилась за сутки, то
часть бутыли. Поскольку вся бутыль наполнилась за сутки, то ![]() составляет
составляет ![]() часть бутыли. При этом в жидкости, выработанной за 1 час, спирт будет составлять
часть бутыли. При этом в жидкости, выработанной за 1 час, спирт будет составлять ![]() от всей бутыли. Следовательно, в итоговом продукте содержание спирта составит
от всей бутыли. Следовательно, в итоговом продукте содержание спирта составит ![]() части бутыли, то есть крепость получившейся смеси равна 72%.
части бутыли, то есть крепость получившейся смеси равна 72%.
Отметим, что если не учитывать условие, что втроём друзья наполнили бутыль ЗА СУТКИ, то получим ответ ![]() =
= ![]() (%). В тех случаях, когда a, b и с связаны условием
(%). В тех случаях, когда a, b и с связаны условием ![]() =
= ![]() , это выражение приводит к ответу 72%.
, это выражение приводит к ответу 72%.
3.2.
Биссектрисы углов A и B выпуклого четырехугольника АВСD пересекаются в точке P, а биссектрисы углов C и D пересекаются в точке Q (точки Q и P различны). Прямая PQ проходит через середину стороны AB. Найдите угол DAB, если Ð ABC = a .Ответ
: a или 180° – a .Так как точка
P принадлежит биссектрисе угла ABC, то она равноудалена от его сторон, то есть от прямых BА и BС, на которых лежат стороны четырехугольника ABCD. Точка Р лежит также и на биссектрисе угла DAB, поэтому она равноудалена от прямых AB и AD (см. рис. 3 а, б). Таким образом, точка Р равноудалена от прямых AD и BС. Аналогично доказывается, что точка Q также равноудалена от прямых AD и BС.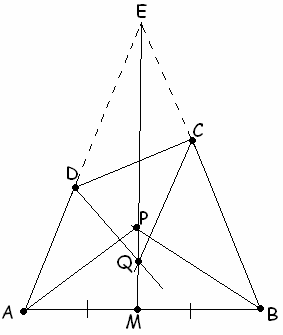
Пусть М – середина стороны АВ. Возможны два случая.
1) Прямые
AD и BС пересекаются в точке Е. Тогда точки P и Q лежат на биссектрисе угла АЕВ (см. рис. 3а). По условию, прямая PQ проходит через точку М, поэтому отрезок ЕМ является биссектрисой и медианой треугольника AEB, значит, этот треугольник равнобедренный, то есть Ð DAB = Ð ABC = a .В случае, когда точка Е лежит в другой полуплоскости относительно прямой АВ,
DAB и ABC – углы, смежные равным углам.2) Прямые AD и BС параллельны (см. рис. 3б).
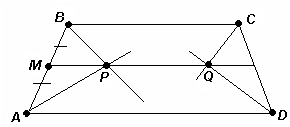
В этом случае, ABCD – параллелограмм или трапеция. Точки P и Q равноудалены от прямых AD и BС (по доказанному выше), поэтому прямая PQ проходит через середины сторон AB и СD. Тогда Ð DAB = 180° – Ð ABC = 180° – a .
3.3. Является ли квадратом какого-нибудь натурального числа произведение первых 2007 простых чисел, увеличенное на 1?
Ответ: нет, не является.
Первый способ. Все простые числа, кроме числа 2, нечётны. Поэтому произведение первых 2007 простых чисел равно нечётному числу, умноженному на 2. Значит, при делении на 4 это произведение даёт остаток 2. После прибавления единицы остаток от деления на 4 станет равен 3.
Докажем, что квадрат натурального числа не может иметь остаток 3 при делении на 4. Действительно, если m – чётное число, то m2 делится на 4, а если m – нечётное число, то оно имеет вид: m = 4n ± 1, где n – натуральное. Тогда m2 = 16n2 ± 8n + 1, то есть m2 при делении на 4 даёт остаток 1. Таким образом, при делении квадрата натурального числа на 4 могут получаться только остатки 0 или 1.
Второй способ. Пусть N – произведение первых 2007 простых чисел и нашлось такое натуральное число m, что m2 = N + 1. Тогда N = (m – 1)(m + 1).
Заметим, что множители в правой части этого равенства имеют одинаковую чётность. Так как
N содержит множитель 2, то N – чётное число, следовательно числа m – 1 и m + 1 также чётные, поэтому и число N должно делится на 4, что невозможно.
Четвертый тур (25 минут; каждая задача – 9 баллов
).4.1.
Рассматриваются все квадратные уравнения вида x2 + px + q = 0 c целыми коэффициентами такие, что p + q = 218. Сколько таких уравнений имеют целые корни?Ответ
: 4 уравнения.Пусть данное уравнение имеет целые корни m и n, причем m ³ n. Тогда, по теореме Виета, m + n = –p; mn = q. По условию, p + q = 218, поэтому – m – n + mn = 218 Û mn – m – n + 1 = 219 Û m(n – 1) – (n – 1) = 219 Û (m – 1)(n – 1) = 73× 3.
Так как в левой части полученного равенства записано произведение двух целых чисел, и
m – 1 ³ n – 1, то возможны четыре варианта:Каждая найденная пара корней определяет ровно одно уравнение, удовлетворяющее условию задачи.
4.2.
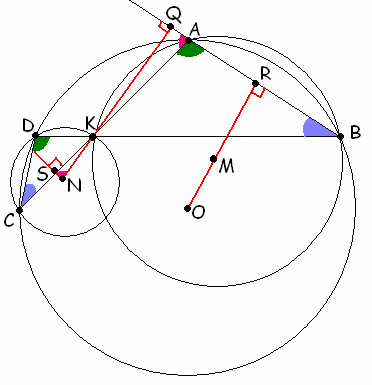
Хорды АС и BD окружности с центром О пересекаются в точке K. M и N – центры окружностей, описанных около треугольников ABK и CDK соответственно. Докажите, что OM = KN.Так как АВ является общей хордой окружностей с центрами О и М, то прямая ОМ ей перпендикулярна (см. рис. 4 а
, б).Первый способ. Докажем, что прямая
KN также перпендикулярна прямой АВ.Действительно, пусть прямые
KN и AB пересекаются в точке Q (см. рис. 4а). Тогда Ð QAK = 180° – Ð BAK = 180° – Ð CDB, так как вписанные углы BAK и CDB опираются на одну и ту же дугу окружности с центром О. Проведем перпендикуляр NS к хорде CK. Тогда угол Ð SNK =Из того, что
KN^ AB и MO^ AB, следует, что прямые MO и KN параллельны. Аналогичным образом доказывается, что прямая ON параллельна прямой MK. Значит, OMNK – параллелограмм, следовательно равны его противоположные стороны, то есть KN = OM, что и требовалось доказать.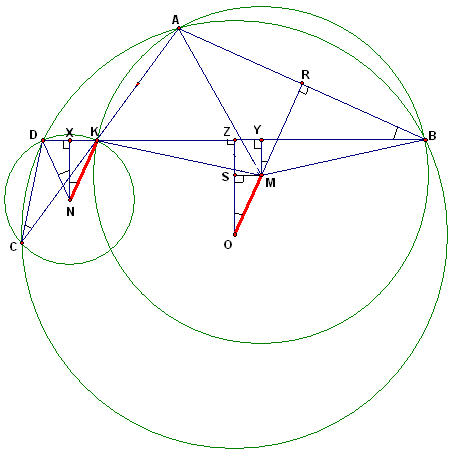
![]()
Пусть
S и R – основания перпендикуляров, опущенных из точки M на отрезки OZ и АВ соответственно. Тогда MSZY – прямоугольник, поэтому SM = ZY.Кроме того, используя свойства вписанных и центральных углов, получим: Ð
XNK =Таким образом, Ð
XNK = Ð SOM и XK = SM, следовательно равны прямоугольные треугольники XNK и SOM. Значит, KN = OM, что и требовалось доказать.
4.3.
На листе клетчатой бумаги в узлах сетки поставили пять точек и каждые две из них соединили отрезком. Могло ли получиться так, что ни один из этих отрезков не содержит внутри себя какого-нибудь из узлов сетки?Ответ
: нет, не могло.Введём декартову систему координат на плоскости так, чтобы координатные оси проходили по линиям сетки и единичный отрезок был равен стороне клетки. В такой системе координат каждый узел сетки является точкой с целочисленными координатами, и наоборот, любая точка с целочисленными координатами является узлом сетки.
Пусть Ч означает, что координата чётна, а Н – что она нечётна. Тогда для узлов сетки возможны ровно четыре комбинации чётностей первой и второй координат: (Ч; Ч), (Н; Ч), (Ч; Н) и (Н; Н).
Следовательно, по принципу Дирихле, среди пяти отмеченных точек найдутся хотя бы две точки
X(x1; x2) и Y(y1; y2), у которых соответствующие координаты одинаковой чётности. Пусть С – середина отрезка XY, тогдаТаким образом, внутри отрезка
XY есть узел сетки.