1.1. Найдите все значения x, для которых .

Ответ: (–1,5; 1,5).

Значение данного квадратного корня отлично от нуля, если это выражение имеет смысл и подкоренное выражение не равно нулю, то есть если 9 – 4x² > 0 Û |x| < 1,5 Û –1,5 < x < 1,5.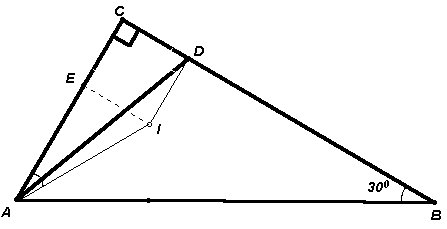

1.2. В треугольник АВС с прямым углом С и углом В, равным 30° , вписана окружность радиуса 1. Найдите расстояние от вершины А до точки касания окружности со стороной ВС.

Ответ: .

Пусть I – центр вписанной окружности, D и E – точки касания этой окружности с катетами ВС и АС соответственно (см. рис. 1). Четырехугольник IECD – квадрат, так как все его углы прямые и ID = IE. Поэтому CD = CE = r = 1.

Первый способ. Проведем отрезок AI. В треугольнике АЕI угол Е – прямой, а Ð ЕАI = 30° (так как AI – биссектриса угла САВ, равного 60° ). Тогда АЕ = = ; АС = АЕ + r = + 1. Из прямоугольного треугольника АСD: AD² = AC² + CD² = 5 + 2.

Второй способ. Из равенства отрезков касательных, проведенных из одной точки к окружности, можно вывести формулу , справедливую для любого прямоугольного треугольника с катетами а и b и гипотенузой с.

В нашем случае: пусть АС = b, тогда ВС = = b; АВ = 2b. Подставив эти выражения в указанное выше равенство, получим уравнение: . Следовательно, . Из прямоугольного треугольника АСD: AD² = AC² + CD² = 5 + 2.

1.3. Сколько натуральных чисел вида 3ⁿ + 1, где n – натуральное число, являются точными квадратами?

Пусть 3ⁿ + 1 = m², где m – натуральное число. Тогда 3ⁿ = (m – 1)(m + 1). Множители правой части отличаются на 2 и являются степенями тройки. Это возможно только в одном случае: если они равны 1 и 3 соответственно, то есть m = 2. Следовательно, условие задачи выполняется только при n = 1.

2.1. Найдите все такие а и b, что уравнения x² + ax + b² = 0 и x² + bx + a² = 0 имеют общий корень.

Ответ: а = b = 0.

Пусть а и b – искомые числа, x – общий корень данных уравнений. Тогда оба уравнения становятся верными равенствами. Вычитая из первого равенства второе, получим: (а – b)x + (b – a)(b + a) = 0 Û (а – b)(x – a – b) = 0 Û a = b или x = a + b.

1) Если a = b, то надо найти все такие а, при которых уравнение x² + ax + a² = 0 имеет корни. Поскольку D = a² – 4a² = –3a² £ 0, то уравнение имеет корни только при а = 0.

2) Если x = a + b, то подставив это значение в любое из уравнений, получим, что 2a² + 3ab + 2b² = 0. Решая это квадратное уравнение относительно переменной а, получим: D = 9b² – 16b² = –7b² £ 0, поэтому полученное равенство выполняется только при а = b = 0.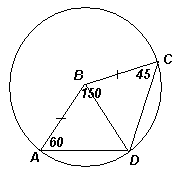

2.2. В выпуклом четырехугольнике АВСD Ð А = 60° , Ð B = 150° , Ð C = 45° и АВ = ВС. Докажите, что треугольник АВD – равносторонний.

В данном четырехугольнике Ð D = 360° – (Ð А + Ð B + Ð C) = 105° . Рассмотрим окружность с центром В и радиусом ВА, проходящую также через точку С (см. рис. 2). Так как Ð ADC + Ð ABC = 180° , то эта окружность проходит через точку D. Тогда треугольник АВD – равнобедренный с углом 60° , то есть АВD – равносторонний.

2.3. Найдите наименьшее натуральное число n такое, что 2n является квадратом натурального числа, а 3n – кубом.

Ответ: 72.

Так как 2n – квадрат натурального числа, то в его разложение на простые множители 2 входит с четным показателем степени. Следовательно, n – четное число. Так как 3n – куб натурального числа, то в его разложение на простые множители как число 2, так и число 3 входят с показателем степени, кратным трем. Поэтому в разложении числа 3n должно быть не менее трех двоек и двух троек, то есть n ³ 8× 9 = 72. Это число удовлетворяет условию задачи: 2n = 144 = 12²; 3n = 216 = 6³.

3.1. Пешеход, велосипедист и мотоциклист движутся в одну сторону с постоянными скоростями. В тот момент, когда пешеход и велосипедист находились в одной точке, мотоциклист был в 6 км позади них. В тот момент, когда мотоциклист догнал велосипедиста, пешеход отставал от них на 3 км. На сколько километров велосипедист обгонял пешехода в тот момент, когда пешехода догнал мотоциклист?

Первый способ («физический»). Будем считать, что пешеход неподвижен. Мотоциклист вначале отставал от пешехода на 6 км, а потом обогнал его на 3 км, а велосипедист вначале находился вровень с пешеходом, а затем обогнал его на 3 км. Следовательно, скорость мотоциклиста относительно пешехода в 3 раза больше скорости велосипедиста относительно пешехода.

Так как мотоциклист, догнав пешехода, проехал относительно пешехода 6 км, то велосипедист проехал относительно пешехода в три раза меньше, то есть 2 км.

Второй способ («алгебраический»). Пусть скорости мотоциклиста, велосипедиста и пешехода равны соответственно а км/ч, b км/ч и c км/ч. Пусть также с момента «встречи» пешехода и велосипедиста до момента «встречи» мотоциклиста и велосипедиста прошло t часов, а с момента «встречи» пешехода и велосипедиста до момента «встречи» пешехода и мотоциклиста прошло T часов. Тогда составляем три уравнения: (a – c)t = 9; (b – c)t = 3; (a – c)T = 6. Найдем искомое расстояние S = (b – c)T. Разделив первое уравнение на второе, получим, что . Тогда , то есть , S = 2.

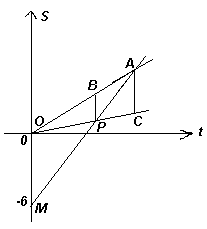
Третий способ («геометрический»). Изобразим графики зависимости перемещения S от времени t для всех участников процесса в одной системе координат (см. рис. 3, лучи ОА, ОС и МА – графики движения велосипедиста, пешехода и мотоциклиста соответственно). Из условия задачи следует, что ОМ = 6; АС = 3.

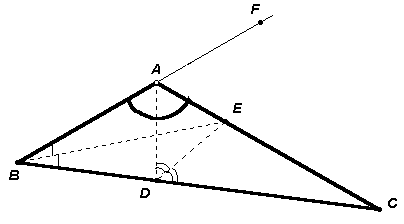
Для того, чтобы найти искомое расстояние ВР, рассмотрим две пары подобных треугольников: D АВР ~ D АОМ, D ОВР ~ D ОАС. Из первого подобия следует, что , а из второго, что . Следовательно, . Тогда .

3.2. В треугольнике АВС проведены биссектрисы AD и ВЕ. Оказалось, что DE – биссектриса треугольника ADC. Найдите угол ВАС.

Ответ: 120° .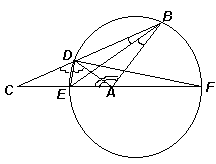

Первый способ. Рассмотрим треугольник АВD, в котором ВЕ – биссектриса внутреннего угла, а DE – биссектриса внешнего угла ADC (см. рис. 4а). Точка Е их пересечения равноудалена от сторон треугольника, поэтому является центром вневписанной окружности (окружности, касающейся стороны AD и продолжений сторон ВА и ВD). Следовательно, АЕ – биссектриса внешнего угла DAF этого треугольника. Таким образом, Ð FAE = Ð EAD = Ð DAB = 60° , поэтому Ð ВАС = 120° .

Второй способ. По свойству биссектрисы треугольника . Следовательно, точки B, E и D принадлежат геометрическому месту точек, отношение расстояний до которых от точек А и С постоянно. Этим геометрическим местом является окружность Аполлония, центр которой лежит на продолжении стороны АС данного треугольника (см. рис. 4б). Рассмотрим EF – диаметр окружности, тогда Ð EDF = 90° . Так как DE – биссектриса угла АDC, то DF – биссектриса угла АDB. Пусть Ð САD = Ð BАD = a , Ð АBE = Ð CBE = b , Ð АDF = Ð BDF = g = Ð BDF (вписанные углы, опирающиеся на одну дугу). Составим систему уравнений, используя сумму углов треугольников АВD и АВЕ: . Выразив b + g из одного уравнения и подставив в другое, получим, что a = 60° , то есть Ð ВАС = 120° .

3.3. На острове есть сеть железнодорожных линий, по которой можно проехать с любой станции на любую. Известно, что среди всех станций есть ровно 20 узловых (в каждую из которых сходятся не менее трех линий) и ровно 21 тупиковая. Докажите, что в сети есть кольцевая линия.

Первый способ. Предположим, что в сети нет «кольца». Рассмотрим одну из тупиковых станций и перегон, ведущий к ней. Если их удалить, то предыдущая станция либо сама станет «тупиком» (если она была «проходной»), либо, если она была «узлом», то станет «проходной» или останется «узлом». В первом случае количества «тупиков» и «узлов» не изменятся, значит, не изменится и их разность. Во втором случае количество «тупиков» уменьшится на один, а количество «узлов» либо не изменится, либо уменьшится на один, поэтому разность между количествами «тупиков» и «узлов» не увеличится. Повторяя эту процедуру, в конце концов мы получим один перегон с двумя «тупиками» на концах. Поэтому изначально в данной сети разность между количествами тупиковых и узловых станций не меньше двух.

Второй способ. Пусть t, p и u – количества тупиковых, «проходных» и узловых станций соответственно. К «тупикам» примыкают t перегонов, к «проходным» станциям – 2p перегонов, а к «узлам» – не меньше, чем 3u перегонов. Так как каждый перегон подсчитан дважды, то общее количество N перегонов железнодорожной сети таково, что 2N ³ t + 2p + 3u. С другой стороны, при отсутствии в сети кольцевых линий, N = t + p + u – 1.

Упростив неравенство 2(t + p + u – 1) ³ t + 2p + 3u, получим, что t – u ³ 2, что и требовалось.

4.1. Положительные числа x, y и z удовлетворяют неравенству x² + y² + z² £ 3. Докажите, что .

Первый способ. Заметим, что при x > 0, y > 0 и z > 0, доказываемое неравенство равносильно тому, что xy + yz + zx ³ xyz(x + y + z).

1) При любых x, y и z выполняется неравенство x² + y² + z² ³ xy + yz + zx, поэтому из неравенства x² + y² + z² £ 3 следует неравенство xy + yz + zx £ 3, а из него, в свою очередь, для положительных x, y и z, следует, что (xy + yz + zx)² £ 3(xy + yz + zx).

2) При любых а, b и с выполняется неравенство (a + b + c)² ³ 3(ab + bc + ca). Введя обозначения xy = а, yz = b и zx = с, получим: (xy + yz + zx)² ³ 3(xy²z + xyz² + x²yz) = 3xyz(x + y + z).

Из неравенств, полученных в пунктах 1) и 2), следует, что , что и требовалось.

Второй способ. При решении задачи используем следующее утверждение: если 0 £ a₁ £ a₂ £ a₃ и 0 £ b₁ £ b₂ £ b₃, то 3(a₁b₃ + a₂b₂ + a₃b₁) £ (a₁ + a₂ + a₃)(b₁ + b₂ + b₃). Для его доказательства можно рассмотреть, например, разность между правой и левой частями, которая равна: a₁b₁ + a₁b₂ + a₂b₁ + a₂b₃ + a₃b₂ + a₃b₃ – 2a₁b₃ – 2a₂b₂ – 2a₃b₁ = a₁(b₁ – b₃) + a₁(b₂ – b₃) + a₂(b₁ – b₂) + a₂(b₃ – b₂) + a₃(b₂ – b₁) + a₃(b₃ – b₁) = (b₃ – b₁)(a₃ – a₁) + (b₂ – b₁)(a₃ – a₂) + (b₃ – b₂)(a₂ – a₁) ³ 0, так как в каждой скобке – неотрицательное число.

Пусть a₁ = x²; a₂ = y²; a₃ = z²; ; ; . Без ограничения общности можно считать, что 0 < x £ y £ z, тогда , то есть эти числа удовлетворяют условию доказанного неравенства.

Используя, кроме него, условие задачи, получим, что £ £ , откуда и следует, что .

4.2. Вася вырезал из бумаги выпуклый четырехугольник c перпендикулярными диагоналями, у которого длины последовательных сторон равны а, b, c и d. Петя тоже вырезал выпуклый четырехугольник с такими же длинами последовательных сторон. Могут ли диагонали Петиного четырехугольника оказаться не перпендикулярными?

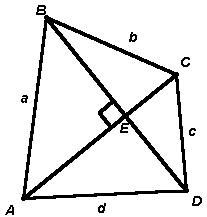
Рассмотрим выпуклый четырехугольник АВСD, в котором диагонали перпендикулярны, Е – точка их пересечения (см. рис. 5а). Применяя теорему Пифагора в каждом из четырех прямоугольных треугольников, получим, что а² + с² = АЕ² + ВЕ² + СЕ² + DE² = b² + d². Следовательно, а² – b² = d² – c².

Так как длины последовательных сторон четырехугольников, вырезанных Васей и Петей, одинаковы, то полученное равенство должно выполняться в обоих четырехугольниках.

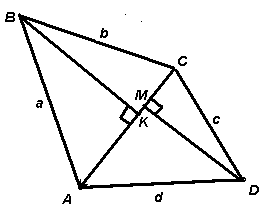
Пусть диагонали Петиного четырехугольника не перпендикулярны (см. рис. 5б). Проведем перпендикуляры BK и DM к диагонали АС. Тогда а² – b² = АK² – CK² = (АK + CK)(АK – CK) = АC(АK – CK) и d² – c² = АM² – CM² = (АM + CM)(АM – CM) = АC(АM – CM). Таким образом получим, что АK – CK = АM – CM Û АK + CM = АM + CK. Это равенство выполняется только в случае, если точки K и M совпадают, то есть диагонали АС и BD этого четырехугольника также перпендикулярны.

Отметим, что в процессе решения задачи было доказано следующее утверждение: диагонали четырехугольника перпендикулярны тогда и только тогда, когда равны суммы квадратов его противолежащих сторон. Доказательство этого утверждения для случая, когда данный четырехугольник – не выпуклый, проводится аналогично. Во второй части доказательства можно также использовать теорему косинусов.

4.3. Тетрадный лист раскрасили в 23 цвета по клеткам. Пара цветов называется хорошей, если существуют две соседние клетки, закрашенные этими цветами. Каково наименьшее количество хороших пар?

Ответ: 22.

Нарисуем на листе путь из горизонтальных и вертикальных звеньев, проходящий через все клетки по одному разу. (Например, начнем с левой верхней клетки, пройдем верхнюю строку, спустимся на одну клетку, пройдем вторую строку справа налево, спустимся еще на одну клетку и так далее.) Пройдем по этому пути, нумеруя цвета в порядке их появления в первый раз. Когда нам впервые встречается k - й цвет (k > 1), мы проходим через хорошую пару цветов (предыдущая клетка окрашена в другой цвет). Эта пара еще не появлялась, поскольку еще не появлялся k - й цвет. Значит, нам встретится не менее, чем 23 – 1 = 22 различных хороших пар цветов.

5.1. Известно, что . Какие значения может принимать выражение (a + b)(b + c)(c + a)?

Ответ: 0.

Преобразуем исходное равенство: Û Û Û Û .

Следовательно, (a + b)(b + c)(c + a) = 0.

5.2. Сумма расстояний между серединами противолежащих сторон четырехугольника равна его полупериметру. Верно ли, что этот четырехугольник – параллелограмм?

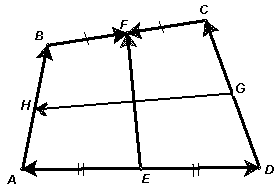
Рассмотрим четырехугольник ABCD. Пусть Е – середина AD, F – середина BC (см. рис. 6). Тогда и . Сложив эти равенства, и используя, что и , получим: .

Аналогично, если точки G и H – середины сторон СD и АВ соответственно, то .

Для любых векторов и справедливо неравенство: , причем равенство достигается тогда и только тогда, когда векторы и сонаправлены. Применяя это, получим, что и . Таким образом, , причем равенство, заданное в условии задачи, достигается т. и т. т., когда и . Это и означает, что ABCD – параллелограмм.

5.3. Набор из 100 чисел таков, что ровно 2006 попарных произведений отрицательны. Сколько нулей в этом наборе?

Ответ: 7.

Пусть в данном наборе x положительных чисел и y отрицательных. Тогда xy = 2006. Разложение 2006 на простые множители имеет вид: 2006 = 2× 17× 59. Так как каждое из чисел x и y меньше ста, то одно из них равно 59, а другое – 34. Следовательно, количество нулей в наборе составляет 100 – 59 – 34 = 7.