10 класс
Первый тур (10 минут; каждая задача – 6 баллов
).1.1.
Известно, что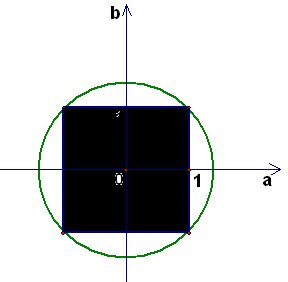
Первый способ
. На координатной плоскости aOb неравенствоПоскольку квадрат вписан в круг, то для всех (а
; b), удовлетворяющих первому неравенству, выполняется и второе неравенство.*График этого неравенства можно, например, получить, рассмотрев всевозможные комбинации знаков значений выражений а + b и а – b (четыре случая).
Второй способ. Так как 2
іТогда
a2 Ј 1 и b2 Ј 1, следовательно,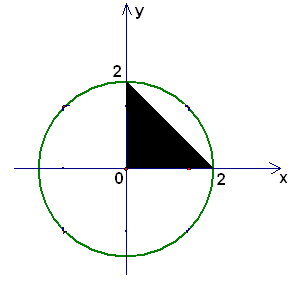
Третий способ
. Возведем обе части данного неравенства в квадрат:Четвертый способ
. Пусть |a + b| = x і 0; |a – b| = y і 0. Тогда«От противного». Пусть это не так, тогда ![]()
«Графически». Система неравенств ![]() задает на координатной плоскости треугольник с вершинами в точках (0; 0); (0; 2); (2; 0), который целиком принадлежит кругу с центром (0; 0) и радиусом
задает на координатной плоскости треугольник с вершинами в точках (0; 0); (0; 2); (2; 0), который целиком принадлежит кругу с центром (0; 0) и радиусом
1.2.
Найдите гипотенузу прямоугольного треугольника, если его сумма катетов равна 12, а сумма косинусов острых углов равнаОтвет
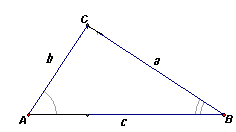
: 6Пусть С – вершина прямого угла треугольника АВС
, ВС = а, АС = b, AB = c (см. рис. 2).Первый способ
. Так как a = cЧ cosР B, b = cЧ cosР A, то a + b = cЧ (cosР A + cosР B). По условию, 12 = с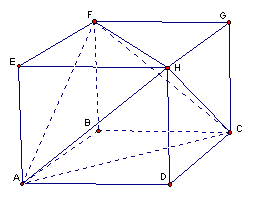
Второй способ
. Так как cosР A + cosР B = cosР A + cos (90° – Р A) = cosР A + sinР A =1.3.
Можно ли разрезать куб на пять треугольных пирамид?Ответ: да, можно.
Пусть дан куб
ABCDEFGH. Искомые пять пирамид – DCAH, EAFH, BACF, GCFH и FACH (см. рис. 3).
Второй тур (15 минут; каждая задача – 7 баллов
).2.1.
Квадратный трехчлен f(x) = x2 + аx + b имеет два корня, один из которых лежит внутри отрезка [0; 1], а другой – вне этого отрезка. Определите знак f(b).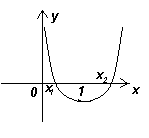
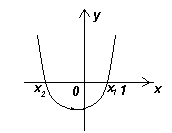
Ответ
: f(b) < 0.Первый способ
. Заметим, что f(b) = b2 + аb + b = b(а + b + 1) = f(0)Ч f(1). График данного трехчлена – парабола, ветви которой направлены вверх. Из условия задачи следует, что числа f(0) и f(1) имеют разные знаки (см. рис. 4 а, б). Следовательно, f(b) < 0.Второй способ
. График данного трехчлена – парабола, ветви которой направлены вверх. Пусть x1О (0; 1), x2П [0; 1]. По теореме Виета x1 Ч x2 = b, значит,1) Если
x2 < 0, то b = x1Ч x2 < 0 и x2 < b. Следовательно, bО (x2; x1), то есть f(b) < 0 (см. рис. 4а).2) Если
x2 > 1, то b = x1Ч x2 > 1 и x2 > b. Следовательно, bО (x1; x2), то есть f(b) < 0 (см. рис. 4б).2.2.
На диагонали АС выпуклого четырехугольника АВСD выбрана точка О так, что OC = OD и Р CОD = 90°. Известно также, что Р AОB = 110° и точка О равноудалена от прямых DA, AB и BC. Найдите углы четырехугольника.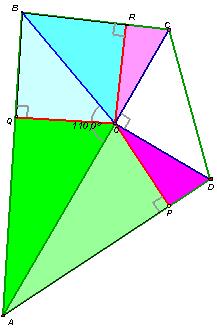
Ответ
: Р A = 50° ; Р B = 90° ; Р C = Р D = 110° .Пусть Р
, Q и R – основания перпендикуляров, опущенных из точки О на прямые DA, AB и BC соответственно (см. рис. 5). Тогда Р и Q – внутренние точки сторон AD и АВ соответственно, поскольку Р AОD = 90° , Р AОB = 110°.По условию, |
OP| = |OQ| = |OR|. Используя признак равенства прямоугольных треугольников по гипотенузе и катету, получим: D OPA = D OQA; D OQB = D ORB; D ORC = D OPD. Значит, при вершине О, помимо прямого угла СОD, есть три пары равных углов, следовательно, 2Р AOQ + 2Р QOB + 2Р ROC + Р COD = 360° . Учитывая, что 2Р AOQ + 2Р QOB = 2Р AOB = 220° , получим, что Р ROC = 25° .Отметим, что если точка R лежит на продолжении стороны ВС, то 2
Р AOQ + 2Р QOB = 2Р AOB = 270° , что противоречит условию.Следовательно, Р RCО = Р PDО = 65° , тогда Р C = Р D = 110° ; Р A = 2Р РAO = 2Р РOD =2Р ROC = 50° ; Р B= 360° – (Р A + Р C + Р D) = 90° .
Подсчет углов можно провести иначе, если использовать, что точка О – центр окружности, касающейся прямых DA
, AB и BC, то есть О – точка пересечения биссектрис углов А и В данного четырехугольника.Пусть
Р BAО = Р DAO = a ; Р ABО = Р CBO = b ; Р BCО = Р ADO = g . Тогда, используя теоремы о сумме углов треугольника и о внешнем угле треугольника, составим систему уравнений: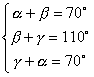 . Решив ее (проще всего способом сложения), получим:
. Решив ее (проще всего способом сложения), получим:  Отсюда сразу следует ответ, приведенный выше.
Отсюда сразу следует ответ, приведенный выше.
2.3.
В верхнем углу таблицы 11ґ 11 стоит число 1, а остальные клетки пусты. Сережа заполняет таблицу по следующему правилу: если в какой-то клетке стоит число x, то он ставит в любую соседнюю (по стороне) пустую клетку либо число 4x, либо число (x – 12), либо число (x + 3). Сможет ли он добиться того, чтобы сумма всех чисел таблицы стала равной нулю?Ответ: нет, не сможет.
Заполнение таблицы начинается с числа 1, и все числа, поставленные Сережей, имеют при делении на 3 остаток 1. Действительно, прибавление числа 3 или вычитание числа 12, очевидно, не меняет остатка от деления на 3, а поскольку 4
x = x + 3x, то и эта операция сохраняет остаток при делении на 3.Следовательно, сумма
S всех чисел таблицы имеет вид: S = 3n +121 = (3n +120) + 1, где nО Z. Таким образом, число S также дает остаток 1 при делении на 3, то есть S № 0.
Третий тур (20 минут; каждая задача – 8 баллов
).3.1.
Найдите наименьшее значение выражения (x + y)(x + z), где x, y и z – положительные числа и xyz(x + y + z) = 1.Ответ
: 2.Первый способ
. Так как x > 0, y > 0, z > 0, то xyz(x + y + z) = 1 Ы yz(x2 + xy + xz) = 1 Ы x2 + xy + xz =Равенство достигается, например, если
y = z = 1, x =Второй способ
. Пусть , тогда
, тогда Докажем, что все сомножители в его левой части – положительные числа. Так как произведение и четвертый множитель положительны, то отрицательными могут быть только ровно два из первых трех множителей. Пусть, например, ![]() и
и ![]() . Сложив эти неравенства почленно, получим, что а < 0 – противоречие. Аналогичный результат получится, если рассмотреть любую другую пару сомножителей.
. Сложив эти неравенства почленно, получим, что а < 0 – противоречие. Аналогичный результат получится, если рассмотреть любую другую пару сомножителей.
Следовательно, существует треугольник со сторонами а
, b и с. Найдем его площадь по формуле Герона:С другой стороны: ![]() . Следовательно, (
. Следовательно, (
3.2.
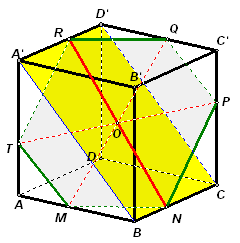
Главные диагонали шестиугольного сечения куба пересекаются в одной точке. Обязательно ли это сечение проходит через центр куба?Ответ: да, обязательно.
Рассмотрим куб АВСDA
’B’C’D’ и какое-нибудь его шестиугольное сечение MNPQRT (см. рис. 6). Предположим, что диагонали RN, MQ и TP шестиугольника пересекаются в некоторой точке О.Первый способ
. Заметим, что прямая RN лежит в плоскости диагонального сечения BCA’D’, а прямая MQ – в плоскости сечения ABC’D’. Следовательно их общая точка О принадлежит BD’ – прямой, по которой пересекаются указанные плоскости. Прямая TP лежит в плоскости сечения АСС’A’, поэтому точка О должна являться пересечением BD’ и этой плоскости. Таким образом, О – центр куба.Второй способ. Противоположные стороны данного сечения попарно параллельны, так как принадлежат прямым пересечения плоскости сечения с противолежащими гранями куба. Следовательно, данное сечение разбивается диагоналями на три пары подобных треугольников:
D МОN ~ D QОR, D NОP ~ D RОT, D PОQ ~ D TОM. ТогдаРассмотрим симметрию пространства с центром О. При этой симметрии образом точки М является точка
R, поэтому образом прямой АВ, проходящей через М, является ей параллельная прямая, проходящая через R, то есть прямая С’D’. Аналогично доказывается, что и остальные прямые, содержащие ребра куба, попарно симметричны относительно О. Таким образом, при симметрии с центром О куб переходит в себя, значит, точка О – центр симметрии куба (точка пересечения диагоналей).Отметим, что во втором способе решения попутно доказан следующий факт: если противолежащие стороны шестиугольника попарно параллельны, а диагонали пересекаются в одной точке, то эта точка – центр симметрии шестиугольника.
3.3.
Найдите все натуральные числа, которые в 11 раз больше суммы своих цифр.Ответ
: 198.Пусть х – одно из искомых чисел, а у – сумма его цифр. По условию х
= 11у, следовательно, х кратно 11.Запишем полученное равенство по-другому: х – у = 10у. Так как числа х и у имеют одинаковые остатки при делении на 9, то число 10у кратно 9. Учитывая, что НОД (10; 9) = 1, получим, что у делится на 9, а значит и х делится на 9. Таким образом, искомое число кратно 99.
Если десятичная запись числа х содержит n разрядов, то х і 10n – 1, с другой стороны х = 11у Ј 11Ч 9n = 99n. Следовательно, должно выполняться неравенство: 10n – 1 Ј 99n. Это справедливо только для трех натуральных значений n: 1; 2 или 3.
Таким образом, х = 99р, где р равно 1, 2 или 3. У всех таких x сумма цифр равна 18, поэтому легко проверить, что решением задачи является только число 198.
Четвертый тур (25 минут; каждая задача – 9 баллов
).4.1.
Известно, что для положительных чисел а, b и c выполняется неравенство:Для положительных чисел а
, b и c неравенство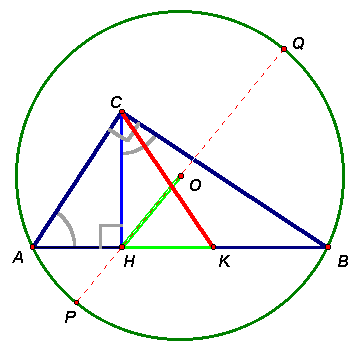
Это неравенство равносильно неравенству (
a + b + c)2 і 3ab + 3bc + 3ca Ы a2 + b2 + c2 і ab + bc + ca. Последнее неравенство выполняется для любых значений переменных, так как оно, в свою очередь, равносильно верному неравенству (a – b)2 + (b – c)2 + (c – a)2 і 0.4.2.
Вершина С прямого угла треугольника АВС лежит внутри окружности с центром О и радиусом R, проходящей через концы гипотенузы АВ, СН – высота треугольника АВС. На прямой АВ взята точка K так, что KН = ОН. Найдите СK.Ответ
: R.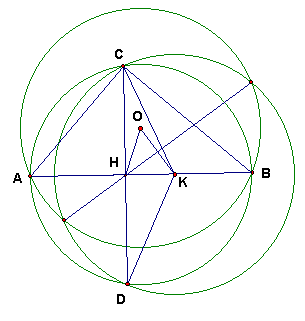
Первый способ
. Из прямоугольного треугольника CHK по теореме Пифагора получим: CK2 = CH2 + KH2 (см. рис. 7а). Высота CH прямоугольного треугольника ABC, проведенная к гипотенузе, является средним геометрическим проекций его катетов на гипотенузу, то есть CH2 = AHЧ BH.Через точку
H проведем диаметр окружности PQ. Тогда, по теореме о произведении отрезков пересекающихся хорд окружности: AHЧ BH = PHЧ QH = (R – OH)(R + OH) = R2 – OH2.Учитывая, что KН
= ОН, получим: CK2 = AHЧ BH + OH2 = R2 – OH2 + OH2 = R2.Таким образом,
CK = R.Второй способ
. Пусть D – образ точки С при симметрии относительно прямой AB (см. рис. 7б). Рассмотрим окружность w 1, описанную около треугольника ABC, и окружность w 2 с центром K и радиусом KC. Заметим, что точки C и D принадлежат обеим окружностям, то есть прямая CD является радикальной осью окружностей w 1 и w 2. Аналогично, прямая AB является радикальной осью данной окружности w и окружности w 1. Следовательно, общая точка H этих прямых является радикальным центром трех окружностей: w , w 1 и w 2, то есть H принадлежит общей хорде окружностей w и w 2. Так как H равноудалена от центров O и K данных окружностей, то радиусы окружностей равны, следовательно, CK = R.4.3. При каких натуральных значениях n числа nn + 1 и (2n)2n + 1 являются простыми одновременно?
Ответ: при n = 1 или n = 2.
При
n = 1 оба данных числа являются простыми: nn + 1 = 2; (2n)2n + 1 = 5.Пусть
n > 1, тогда докажем, что n должно быть натуральной степенью числа 2. Пусть это не так, то есть n = 2kЧ p, где k – натуральное число или ноль, p – нечетное число, отличное от 1. Тогда nn + 1 =Таким образом,
n = 2m, где mО N. Тогда nn + 1 =Проведя рассуждения «от противного», аналогичные предыдущим (то есть предположив, что
m или m + 1 имеют нечетный натуральный делитель, отличный от 1), получим, что рассматриваемые числа могут являться простыми только в том случае, когда оба числа m и m + 1 являются натуральными степенями числа 2.Это возможно только при т = 1. Тогда оба данных числа действительно являются простыми:
nn + 1 = 5 и (2n)2n + 1 = 257.
Пятый тур (15 минут; каждая задача – 7 баллов
).5.1.
Существует ли такая функция f(t), где tО [–1; 1], что для всех xО [0; p ] выполняется равенство f(cosx) = sinx?Ответ
: да, существует.Например, пусть ![]() , тогда
, тогда ![]() , так как для всех xО [0; p ] выполняется неравенство sinx і 0.
, так как для всех xО [0; p ] выполняется неравенство sinx і 0.
5.2. Три высоты остроугольного треугольника пересекаются в точке H, которая делит одну из высот пополам, а другую в отношении 2 : 1, считая от вершины. В каком отношении точка H делит третью высоту?
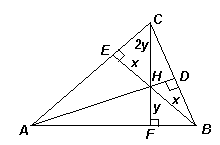
Ответ: 5 : 1.
Первый способ
. Пусть АВС – данный треугольник; AD, BE и CF – его высоты, BH = HE = x, HF = y, CH = 2y (см. рис. 8а).Так как
Р ВЕС = Р ВFС = 90° , то точки B, F, E и С лежат на одной окружности, поэтому BHЧ HE = CHЧ HF. Тогда x2 = 2y2, то естьПрямоугольные треугольники
ADC и АЕН подобны, поэтому
Вычислив отношения, в которых точки Е и F делят стороны АС и АВ, можно было также воспользоваться теоремой Ван – Обеля, которая в данном случае записывается так: ![]()
Второй способ
. Эта задача является частным случаем классического утверждения элементарной геометрии, которое называется теоремой Жергонна: «Если Р – внутренняя точка треугольника АВС, а прямые АР, ВР и СР пересекают противолежащие стороны в точках А1, В1 и С1 соответственно, тоВ нашем случае: треугольник АВС – остроугольный, значит, ортоцентр Н – его внутренняя точка, ![]()
Теорема Жергонна может быть доказана, например, так. Опустим перпендикуляры ![]() и
и ![]() на сторону ВС. Тогда
на сторону ВС. Тогда ![]() (теорема Фалеса или подобие прямоугольных треугольников). С другой стороны,
(теорема Фалеса или подобие прямоугольных треугольников). С другой стороны, ![]() , так как эти треугольники имеют общее основание ВС. Следовательно,
, так как эти треугольники имеют общее основание ВС. Следовательно, ![]() . Выразив аналогичным образом два других отношения, получим:
. Выразив аналогичным образом два других отношения, получим: ![]() и
и ![]()
Следовательно, ![]()
Ответ в задаче можно получить, не ссылаясь на теорему Жергонна. Достаточно провести рассуждения об отношении площадей из второй части доказательства теоремы.
Отметим, что теорема Жергонна обобщается для случая, когда точка Р лежит вне треугольника. Для этого вводится понятие отношения длин направленных отрезков. Тогда теорема Жергонна записывается в единой для всех случаев форме: 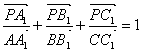
5.3. На дискотеку пришло некоторое количество мальчиков и девочек, всего – не более 40 человек. Каждая девочка бросила взгляд на каждого знакомого мальчика, а каждый мальчик бросил взгляд на каждую незнакомую ему девочку. Всего было брошено 117 взглядов. Сколько мальчиков могло быть на этой дискотеке?
Ответ: мальчиков могло быть либо 9, либо 13.
Пусть на дискотеку пришли х мальчиков и у девочек. По условию х + у Ј 40. Рассмотрим произвольную пару, состоящую из мальчика и девочки. Если они знакомы, то в такой паре будет брошен взгляд девочки на мальчика, а если не знакомы, то будет брошен взгляд мальчика на девочку. То есть каждой паре соответствует ровно один взгляд. Общее количество таких пар (а значит, и взглядов) равно ху.
По условию ху = 117. Число 117 раскладывается на два натуральных множителя тремя способами: 117 = 1
Ч 117 = 3Ч 39 = 9Ч 13. Так как сумма множителей должна быть не больше, чем 40, то возможен только последний вариант. Значит, х = 9 или х = 13.