11 класс
Первый тур (10 минут; каждая задача – 6 баллов
).1.1.
На доске после урока алгебры остались график функции y = x2 и 2007 прямых, параллельных прямой y = x, каждая из которых пересекает параболу в двух точках. Найдите сумму абсцисс точек пересечения прямых и параболы.Ответ
: 2007.Любая прямая, параллельная
y = x, задается уравнением y = x + k, где kО R. Если такая прямая пересекает параболу y = x2 в двух точках, то уравнение x2 = x + k имеет два корня. Это уравнение равносильно квадратному уравнению x2 – x – k = 0, сумма корней которого равна 1. Следовательно, для каждого значения k сумма абсцисс точек пересечения прямой и параболы равна 1, то есть искомая сумма равна 2007.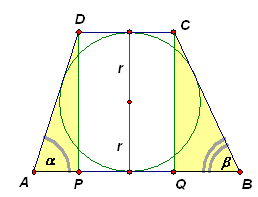
1.2.
В трапецию вписан круг радиуса r. Найдите площадь трапеции, если углы при большем основании равны a и b .Ответ
:Пусть АВ – большее основание трапеции АВСD
, Р DAB = a , Р CBA = b (см. рис. 1). Проведем высоты трапеции DP и CQ, каждая из которых равна диаметру вписанного круга. Треугольники ADP и BCQ – прямоугольные, поэтомуТак как данная трапеция – описанная, то АВ + CD = AD + BC. Следовательно, ![]()
1.3.
На координатной плоскости проведены 11 прямых и отмечены все точки их попарного пересечения. Могло ли оказаться так, что на каждой из прямых лежит ровно 5 точек с положительными абсциссами и ровно 5 точек с отрицательными абсциссами?Ответ: нет, не могло.
Пусть указанное условие выполнено. Тогда найдем, например, общее количество точек с положительными абсциссами. Прямых – 11, на каждой из них – 5 точек, поэтому всего таких точек ![]() (поскольку при таком подсчете каждая точка учтена дважды). Получаем противоречие, так как полученное число не является целым.
(поскольку при таком подсчете каждая точка учтена дважды). Получаем противоречие, так как полученное число не является целым.
Второй тур (15 минут; каждая задача – 7 баллов
).2.1.
Равноускоренно движущийся автомобиль увеличивает свою скорость на некотором прямолинейном участке дороги с v1 до v2. Найдите скорость автомобиля в середине этого участка.Ответ
:Пусть
v – искомая скорость автомобиля в середине участка, t – время, за которое автомобиль преодолел половину пути, T – время, за которое он проделал весь путь.Первый способ. Рассмотрим координатную прямую, направление которой совпадает с направлением движения автомобиля, а начало отсчета совпадает с началом рассматриваемого участка дороги. Тогда: ![]() и
и ![]() , где
, где
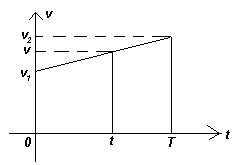
Пусть
S – длина половины участка, тогда: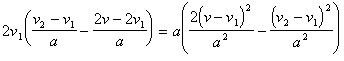 Ы
Ы 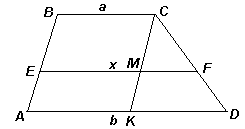
Второй способ
. Рассмотрим график зависимости скорости автомобиля от времени на заданном участке, считая, что v1 – начальная скорость автомобиля (см. рис. 2а). Тогда путь, пройденный автомобилем в каждый момент времени, равен площади трапеции, ограниченной построенным графиком, осями координат и вертикальной прямой, соответствующей выбранному моменту времени.Путь, пройденный за время
t, в два раза меньше пути, пройденного за время T, то есть искомая скорость равна длине отрезка, параллельного основаниям трапеции и делящего ее площадь пополам. Его длина равна среднему квадратичному длин оснований трапеции*, то есть*Пусть АВСD – произвольная трапеция, длины оснований BC и AD которой равны а и b (a < b, см. рис. 2б). Пусть также отрезок EF длины x с концами на боковых сторонах трапеции делит ее площадь пополам. Докажем, что ![]()
Действительно, проведем через вершину С прямую, параллельную АВ, которая пересекает отрезок EF в точке М, а отрезок AD в точке K. Из подобия треугольников CKD и CMF получим, что ![]() , то есть
, то есть ![]() . Кроме того,
. Кроме того, ![]() и
и ![]() , где Н и h – высоты этих трапеций, причем
, где Н и h – высоты этих трапеций, причем ![]() . Так как
. Так как ![]() , то
, то ![]()
2.2. Точки А, В, C и D расположены в пространстве так, что АС = 10, ВD = 8, а расстояние между серединами отрезков АВ и CD равно 9. Верно ли, что данные точки лежат в одной плоскости?
Ответ: да, верно.
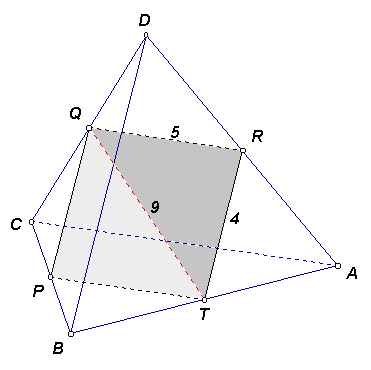
Первый способ. Предположим, что данные точки не лежат в одной плоскости, тогда они являются вершинами тетраэдра ABCD. Пусть точки P, Q, R и T – середины ребер BC, CD, DA и AB соответственно (см. рис. 3а). Четырехугольник PQRT – параллелограмм, в котором QR = ![]() AC = 5, RT =
AC = 5, RT = ![]() BD = 4. Так как диагональ QT = 9, то для треугольника QRT получим: QR + RT = QT, что противоречит неравенству треугольника.
BD = 4. Так как диагональ QT = 9, то для треугольника QRT получим: QR + RT = QT, что противоречит неравенству треугольника.
Таким образом, точки А, В, C и D лежат в одной плоскости.
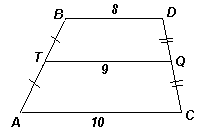
Отметим, что ситуация, описанная в условии, возможна, если АВDC – трапеция с основаниями ВС и AD (см. рис. 3б), но доказывать это не требуется.
Второй способ. Пусть точки T и Q – середины отрезков АВ и CD соответственно, тогда ![]() .
.
Действительно, ![]()
Следовательно, ![]() . По условию:
. По условию: ![]()
2.3.
Натуральное число А имеет ровно три делителя, а натуральное число В – 5 делителей. Сколько делителей может иметь произведение чисел А и В?Ответ
: 7 или 15.Первый способ. Воспользуемся следующим утверждением: если натуральное число ![]() , где все
, где все ![]() – простые числа, а все
– простые числа, а все ![]() – натуральные числа или ноль, то количество делителей числа N равно
– натуральные числа или ноль, то количество делителей числа N равно ![]() .
.
Действительно, каждый делитель числа
N является произведением одних и тех же простых множителей, причем показатель степени множителяРазложим каждое из чисел А и В на простые множители. По условию, для числа А указанное произведение равно 3. Следовательно,
m = 1,Если
p = q, то число AЧ B = p6, и у него 7 делителей. Если p № q, то число AЧ B = p2Ч q4 и оно имеет (2 + 1)(4 + 1) = 15 делителей.Второй способ. Заметим, что каждое из данных чисел имеет нечетное количество делителей. Это означает, что оба числа являются точными квадратами (в противном случае все делители числа можно разбить на непересекающиеся пары).
Поскольку любое натуральное число имеет хотя бы два делителя, то три делителя может иметь только квадрат простого числа, то есть А
= p2, где р – простое. Предположим, что В имеет более одного простого делителя, тогда оно делится на число С =Дальнейшее рассуждение совпадает с уже описанным.
Третий тур (20 минут; каждая задача – 8 баллов
).3.1.
Углы a , b и g некоторого треугольника удовлетворяют равенству cos3a + cos3b + cos3g = 1. Докажите, что один из углов этого треугольника равен 120° .Без ограничения общности можно считать, что
a Ј b Ј g , тогда a и b – острые углы. Преобразуем данное равенство: cos3a + cos3b + cos3g = 1 Ы cos3a + cos3b = 1 – cos3g ЫСледовательно, ![]()
Учитывая, что
a + b < 180° , получим:3.2.
Высота прямоугольного треугольника делит его на два треугольника, периметры которых равны m и n. Найдите периметр данного треугольника.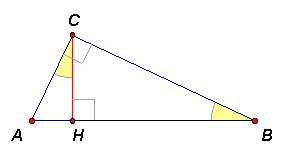
Ответ
:Пусть АВС – прямоугольный треугольник, СН – его высота (см. рис. 4).
Первый способ. Каждый из треугольников
ACH и СBH подобен треугольнику АВС (по двум углам). Коэффициенты этих подобий равны соответственноВторой способ
. Обозначим: Р СВA = Р AСН = b ; СН = h (см. рис. 4). ТогдаВыражая
h из соотношения (1) и подставляя найденные значения синуса и косинуса, получим:Тогда ![]()
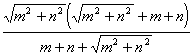 =
= 3.3.
Каждое целое число покрасили в один из двух цветов: синий или желтый. Верно ли, что найдутся два различных числа одного цвета, среднее арифметическое которых – целое число того же цвета?Ответ: да, верно.
Предположим, что все четные числа, большие или равные 2
n, где n – какое-то натуральное число, покрашены в один и тот же цвет. Так как любое четное число является средним арифметическим двух соседних с ним четных чисел, то все четные числа начиная с 2n + 2 – средние арифметические чисел того же цвета.Пусть теперь имеются сколь угодно большие четные числа каждого цвета. Тогда найдется синее число 2
m, такое что 2m + 2 – желтое, и желтое число 2n > 2m + 2 такое, что число 2n + 2 – синее. Среднее арифметическое чисел 2m и 2n + 2 равно m + n + 1 и равно среднему арифметическому чисел 2m + 2 и 2n. Так как первая пара чисел – синяя, а вторая пара – желтая, то число m + n + 1 совпадает по цвету с одной из них.
Четвертый тур (25 минут; каждая задача – 9 баллов
).4.1.
Найдите наибольшее значение выраженияОтвет
: 2.Рассмотрим функцию ![]() . Ее областью определения является [0; 1].
. Ее областью определения является [0; 1].
Первый способ. Воспользуемся формулой ![]() , где
, где ![]()
Преобразовать разность радикалов можно было и по-другому, используя двукратное освобождение от иррациональности в числителе: 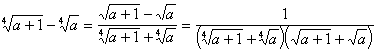
Можно также было доказать убывание функции ![]() с помощью производной. Действительно,
с помощью производной. Действительно, 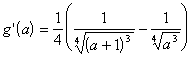 < 0 при a
< 0 при a
Второй способ
. Докажем, что при всех аО [0; 1]Пусть ![]()
Равенство в нем достигается при а = 0, поэтому 2 – наибольшее значение данного выражения.
Неравенство ![]() можно доказать иначе. Например, методом «от противного». Предположим, что (в тех же обозначениях) x + y > 2, тогда 2x
можно доказать иначе. Например, методом «от противного». Предположим, что (в тех же обозначениях) x + y > 2, тогда 2x
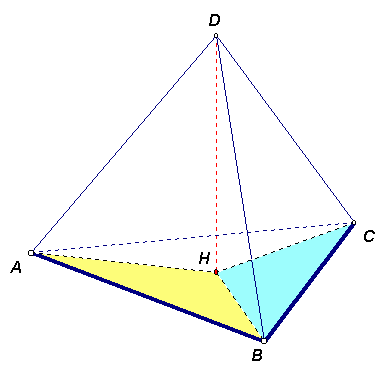
4.2.
В треугольной пирамиде ABCD плоские углы при вершине D прямые, а Н – основание высоты, опущенной из этой вершины. Известно, что отношение площадей треугольников АНВ и ВНС равно k. Найдите отношение площадей граней АDB и BDC.Ответ
:Пусть
a и g – величины двугранных углов при ребрах ВС и АВ соответственно (см. рис. 5). Так как треугольники АНВ и ВНС являются ортогональными проекциями граней АDB и BDC на плоскость АВС, то по теореме о площади ортогональной проекцииТак как все плоские углы при вершине
D – прямые, то, в силу признака перпендикулярности прямой и плоскости, ребра AD, BD и CD перпендикулярны плоскостям BCD, ADC и ADB соответственно. Следовательно, ортогональными проекциями треугольника АВС на плоскости BCD и ABD являются грани BCD и ABD соответственно. Еще раз воспользовавшись теоремой о площади ортогональной проекции, получим:Подставим полученное соотношение в правую часть равенства (1), тогда 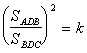 , то есть
, то есть ![]()
4.3.
На клетчатой бумаге нарисован прямоугольник, в котором m строк и n столбцов, причем m Ј n. Диагональ этого прямоугольника пересекает ровно 25 его клеток. Найдите все возможные значения (m; n).Ответ
: (1; 25), (3; 23), (5; 21), (7; 19), (9; 17), (11; 15), (5; 25), (25; 25).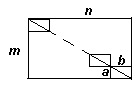
Пусть наибольший общий делитель чисел
m и n равен d. ТогдаРассмотрим
d малых прямоугольников, у которых одна из диагоналей принадлежит диагонали исходного прямоугольника (см. рис. 6). Если она проходит через какой-то узел сетки внутри малого прямоугольника, то она является также диагональю прямоугольника размера xґ y, где 0 < x < a иТаким образом, внутри малого прямоугольника диагональ не проходит через узлы сетки. Поэтому она пересекает
a – 1 горизонтальных линий сетки и b – 1 вертикальных. При движении по диагонали каждое такое пересечение означает переход в новую клетку. Учитывая также клетку, находящуюся в начале движения, получим, что диагональ малого прямоугольника пересекает (a – 1) + (b – 1) + 1 = a + b – 1 клеток. Тогда диагональ большого прямоугольника проходит через d(a + b – 1) клеток. По условию это число равно 25. Так как оно делится на d, то d может быть равно 1, 5 или 25.При
d = 1 получим, что a + b = 26. При этом a и b взаимно просты, a Ј b и m = a, n = b. Любая такая пара (m; n) удовлетворяет условию задачи, и мы получаем первые шесть ответов. При d = 5 имеем: a + b = 6, m = 5a, n = 5b и аналогично предыдущему получаем m = 5, n = 25. При d = 25 точно так же получаем a + b = 2, m = n = 25.
Пятый тур (15 минут; каждая задача – 7 баллов
).5.1.
Может ли многочлен 2x4 + 8x3 + 12x2 + 8x + 1 являться суммой квадратов каких-либо двух многочленов?Ответ: нет, не может.
Пусть
f(x) = 2x4 + 8x3 + 12x2 + 8x + 1 и f(x) = g2(x) + h2(x), где g(x) и h(x) – какие-то многочлены. Тогда, при всех действительных значениях x выполняется неравенство f(x) і 0. С другой стороны, f(–1) = –1 < 0.Полученное противоречие показывает, что
f(x) нельзя представить в виде суммы квадратов двух многочленов.5.2.
Равносторонние треугольники ABC и DFЕ распложены на плоскости так, что вершина В лежит внутри отрезка DE, а вершина F – внутри отрезка АС. Определите вид четырехугольника, вершинами которого являются точки А, С, D и E.Ответ
: трапеция или параллелограмм.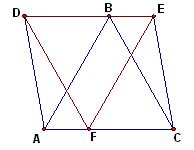
Проведем отрезок BF. Без ограничения общности можно считать, что точки A и D лежат в одной полуплоскости относительно прямой BF, а точки С и Е – в другой (см. рис. 7а). Докажем, что AD и CE параллельны.
Так как Р BAF = Р BDF = 60° , то четырехугольник ADBF – вписанный. Аналогично, из равенства углов BСF и BЕF следует, что вписанным является четырехугольник BECF.
По свойству вписанного четырехугольника
Р ADB + Р AFB = 180° и Р BEC + Р BFC = 180° . Кроме того, Р AFB и Р BFC – смежные.Следовательно,
Р ADB + Р BEC = 360° – (Р AFB + Р BFC) = 180° , то есть AD || CE.Таким образом, в общем случае
ADEC – трапеция, а если AС || DE (то есть данные треугольники равны), то ADEC – параллелограмм (см. рис. 7б).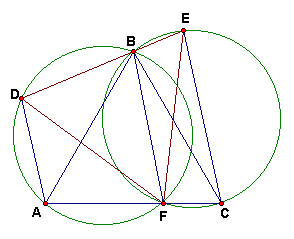
5.3.
В тетраэдре около каждой вершины записали целое число. Около каждого ребра записали число, равное сумме чисел на его концах, а в каждой грани записали число, равное сумме чисел в вершинах грани. Могут ли на ребрах оказаться шесть последовательных целых чисел, а на гранях – четыре последовательных целых числа?Ответ: нет, не могут.
Пусть
S – сумма чисел, записанных в вершинах тетраэдра. Поскольку число, записанное на ребре, равно сумме чисел, записанных на его концах, и из каждой вершины исходит три ребра, то сумма чисел, записанных на ребрах, равна 3S. Аналогично, сумма чисел, записанных на гранях, также равна 3S, поскольку в каждой грани записана сумма чисел, записанных в вершинах, а каждая вершина принадлежит трем граням.Предположим, что условие, о котором спрашивается в задаче, выполнено. Тогда сумма некоторых шести последовательных целых чисел равна сумме четырех последовательных целых чисел. Но первая из этих сумм – это сумма трех четных и трех нечетных чисел, и поэтому она нечетна. А вторая сумма – это сумма двух четных и двух нечетных чисел, и поэтому она четна. Следовательно, две такие суммы равными быть не могут.