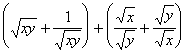 ³
³
9 класс
Первый тур (10 минут; каждая задача – 6 баллов
).1.1.
Про коэффициенты линейной функции у = kх + b известно, что k + b > 0, а 2k + b < 0. Может ли график этой функции пересекать ось абсцисс в точке х = 3?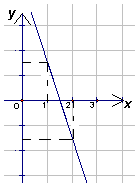
Ответ
: нет, не может.Первый способ. Графиком линейной функции является прямая, которая либо совпадает с осью x, либо имеет с ней не более одной общей точки.
Из условия следует, что k + b = y(1) > 0, а 2k + b = y(2) < 0, то есть график пересекает ось абсцисс в точке x0Î (1; 2) (см. рис. 1).
Второй способ
. Пусть (3; 0) – точка пересечения графика с осью абсцисс. Тогда выполняется равенство 3k + b = 0. Так как 3k + b = 2k + (k + b) = k + (2k + b), то из условия k + b > 0 следует, что 2k < 0, а из условия 2k + b < 0 следует, что k > 0.Полученное противоречие показывает, что наше предположение неверно.
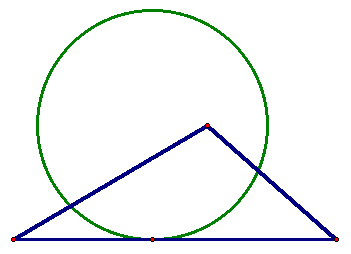
1.2.
Каждая сторона треугольника имеет с окружностью ровно одну общую точку, отличную от вершины. Обязательно ли эта окружность – вписанная?Ответ: нет, не обязательно.
Например, см. рис. 2.
|
Ä |
Ä |
||||
|
Ä |
Ä |
||||
|
Ä |
Ä |
||||
1.3.
Можно ли на некоторые клетки доски 6´ 6 положить по камешку так, чтобы количество камешков в каждой горизонтали было четно, а количество камешков в каждой вертикали – нечетно?Ответ
: да, можно.Например, см. рис. 3. В каждом столбце доски – по одному камешку, а в каждой строке – либо 2 камешка, либо 0.
Второй тур (15 минут; каждая задача – 7 баллов
).2.1.
Сократите дробьОтвет
:Первый способ
. Из условия следует, чтоТогда:
Второй способ
. Для того, чтобы дважды получить выражение2.2. В прямоугольном треугольнике отношение радиусов вписанной и описанной окружностей равно 2 : 5. Найдите отношение катетов.
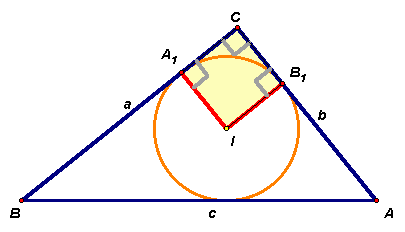
Ответ: 3 : 4.
Пусть в прямоугольном треугольнике больший катет равен а, меньший катет –
b, гипотенуза равна с. Тогда радиус R описанной окружности равен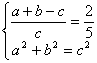 .
.
Обозначим:
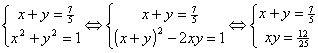 .
.
По теореме, обратной теореме Виета, числа
x и y являются корнями квадратного уравненияФормулу
2.3.
В клетки таблицы 3´ 3 расставлены все цифры от 1 до 9 и подсчитана сумма чисел в каждой строке. Какое наибольшее количество таких сумм могло быть точными квадратами?|
1 |
2 |
6 |
9 |
|
3 |
4 |
9 |
16 |
|
5 |
7 |
8 |
20 |
Ответ
: две суммы.В виде сумм трех цифр от 1 до 9 можно представить только два точных квадрата: 9 и 16, так как 4
< 1 + 2 + 3, а 25 > 7 + 8 + 9. Значит, три суммы в строках могут оказаться точными квадратами только тогда, когда одно из чисел 9 или 16 повторится хотя бы дважды. Это невозможно, так как сумма всех цифр от 1 до 9 равна 45, но 9 + 9 + 16 < 9 + 16 + 16 < 45, а 16 + 16 + 16 > 45.Один из возможных примеров двух сумм, являющихся точными квадратами, показан в таблице.
Третий тур (20 минут; каждая задача – 8 баллов
).3.1.
Представьте многочлен 3x4 + 1 в виде суммы квадратов трех многочленов ненулевой степени с целыми коэффициентами.Ответ: например, 3
x4 + 1 = (x2 + x)2 + (x2 – x)2 + (x2 – 1)2.Можно доказать, что такое представление – единственное
(с точностью до замены любого из многочленов на ему противоположный).Действительно, пусть 3
x4 + 1 = P2(x) + Q2(x) + R2(x), где P, Q и R – многочлены с целыми коэффициентами. Тогда каждый из них должен иметь вторую степень, причем коэффициент при x2 у каждого многочлена должен быть равен ± 1. Кроме того, только один из этих многочленов может иметь свободный член, отличный от нуля, который должен быть равен ± 1.Таким образом,
P(x) = ± x2 + ax; Q(x) = ± x2 + bx; R(x) = ± x2 + cx ± 1. Тогда P2(x) + Q2(x) + R2(x) = 3x4 ± 2(a ± b ± c)x3 + (a2 + b2 + c2 ± 2)x2 ± 2cx + 1. Следовательно,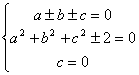 . Учитывая, что а и b – целые числа, получим: с = 0; a = ±
1; b = ±
1.
. Учитывая, что а и b – целые числа, получим: с = 0; a = ±
1; b = ±
1.
При этом в левой части второго равенства должно стоять число –2, а это означает, что
R(x) = ± (x2 – 1); P(x) = ± (x2 + x); Q(x) = ± (x2 – x), что и требовалось доказать.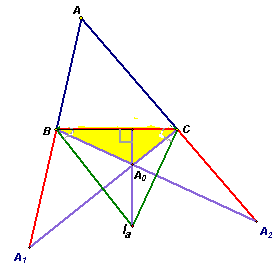
3.2.
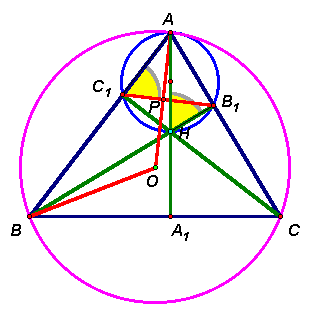
Дан треугольник АВС. На лучах АВ и АС (вне треугольника) построены точки А1 и А2 соответственно так, что ВА1 = СА2 = ВС. А0 – точка пересечения отрезков ВА2 и СА1. Докажите, что прямая, проходящая через А0 перпендикулярно прямой ВС, содержит центр вневписанной окружности треугольника АВС. (Напомним, что вневписанной называется окружность, касающаяся стороны треугольника и продолжений двух других сторон.)Пусть
I – центр окружности, вписанной в треугольник АВС, Ia – центр вневписанной окружности, касающейся стороны ВС (см. рис. 5 а, б).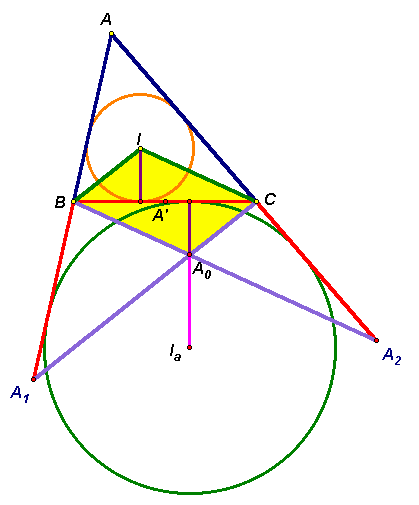
Первый способ
. ВIa и СIa – биссектрисы внешних углов В и С данного треугольника. По условию, треугольники А1BC и А2CB – равнобедренные, поэтому ВIa^ А1C и СIa^ А2В (см. рис. 5а). Следовательно, Ia – точка пересечения двух высот треугольника А0BC, значит третья высота этого треугольника лежит на прямой А0Ia, то есть А0Ia^ ВC, что и требовалось доказать.Второй способ. Так как треугольник А
1ВС – равнобедренный, тоПоэтому основания перпендикуляров, опущенных из точек
I и А0 на отрезокСледовательно, эта прямая содержит центр
Ia вневписанной окружности.3.3.
Можно ли числа 1, 2, ..., 20 расставить в вершинах и серединах ребер куба так, чтобы каждое число, стоящее в середине ребра, равнялось среднему арифметическому чисел, стоящих на концах этого ребра?Ответ: нет, нельзя.
Числа, стоящие на концах каждого ребра, должны быть одинаковой четности, иначе их среднее арифметическое не будет целым. Значит, числа, стоящие в вершинах куба, либо все четные, либо все нечетные. Тогда, хотя бы одно из чисел 1 или 20 (наименьшее или наибольшее) должно стоять в середине какого-то ребра. Но, если а
£ b, то а £Четвертый тур (25 минут; каждая задача – 9 баллов
).4.1.
Найдите все положительные решения уравнения x(x + 1)2 + y(y + 1)2 = 8xy.Ответ
: (1; 1).Первый способ
. В левой части уравнения прибавим и вычтем выражение 4x2 +4у2. Получим: x(x + 1)2 – 4x2 +y(y + 1)2 – 4у2 + 4x2 + 4у2 – 8xy = 0 Û x(x2 + 2х +1) – 4x2 + y(y2 + 2у + 1) – 4у2 + 4(x2 + у2 – 2xy) = 0 Û x(x2 – 2х+1) + y(y2 – 2у + 1) + 4(x – у)2 = 0 Û x(x – 1)2 + y(y – 1)2 + 4(x – у)2 = 0.Так как х и у – положительные числа, то каждое из слагаемых, полученных в левой части уравнения, неотрицательно. Их сумма равна нулю тогда и только тогда, когда каждое слагаемое равно нулю, то есть, если х
= у = 1.Второй способ
. Для любых х и у выполняются неравенства: (x + 1)2 ³ 4x и (y + 1)2 ³ 4y. Тогда, при x > 0 и y > 0 x(x + 1)2 + y(y + 1)2 ³ 4x2 + 4y2 ³ 8xy, так как x2 + y2 ³ 2xy.Равенство достигается т. и т. т., когда х
= у = 1.Третий способ
. Учитывая, что x > 0 и y > 0, разделим обе части уравнения на выражение 2xy. Получим: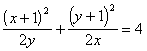 .
.
Оценим левую часть полученного уравнения, используя неравенство о среднем арифметическом и среднем геометрическом, а также неравенство о сумме двух взаимно обратных чисел:
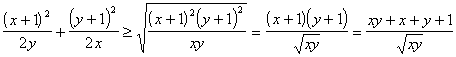 =
= 
= 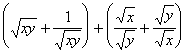 ³
³
4.2.
В остроугольном треугольнике АВС проведены высоты АА1, BB1 и CC1. Через вершины А, В и С проходят прямые, перпендикулярные отрезкам B1C1, C1А1 и А1B1 соответственно. Докажите, что эти три прямые пересекаются в одной точке.Докажем, что эти прямые будут пересекаться в центре О окружности, описанной около треугольника АВС
(см. рис. 6 а, б). Пусть Н – ортоцентр (точка пересечения высот) треугольника АВС.Первый способ
. Треугольник ВОА – равнобедренный, Ð ВОА = 2Ð ВСА, поэтому,Из условия следует, что Ð
HC1A = Ð HB1A = 90° , поэтому четырехугольник AC1HB1 – вписанный. Следовательно, Ð AC1B1 = Ð AHB1 = 90° – Ð A1AC = Ð C. Таким образом, в треугольнике АС1Р (Р – точка пересечения прямых АО и В1С1) сумма двух углов равна 90° , то есть АО^ В1С1. Аналогично доказывается, что ВО^ С1А1 и СО^ А1В1.Равенство углов
AC1B1 и АСВ можно получить иначе, например, из того, что треугольники AB1C1 и АВС подобны (общий угол А и пропорциональность двух сторон).Второй способ. Рассмотрим точки А2, В2 и С2, симметричные точке Н относительно сторон ВС, АС и АВ соответственно (см. рис. 6б). Эти точки лежат на окружности, описанной около треугольника АВС. Кроме того, треугольник А2В2С2 получается из треугольника А1В1С1 гомотетией с центром Н и коэффициентом 2, поэтому стороны этих треугольников соответственно параллельны.
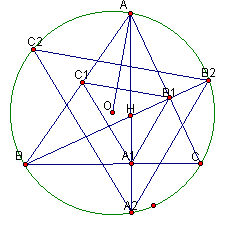
Доказав (одним из уже предложенных способов) равенство Ð ВА1С1 = Ð ВАС = Ð СА1В1 и учитывая, что АА1^ ВС, получим, что Ð АА1С1 = Ð АА1В1, поэтому точка А является серединой дуги В2С2. Следовательно, ОА^ В2С2, то есть АО^ В1С1. Аналогично доказывается, что ВО^ С1А1 и СО^ А1В1.
Отметим, что для тупоугольного треугольника утверждение задачи также справедливо. Более того, как следует из первого способа решения, прямые АО и АН образуют равные углы со сторонами АВ и АС соответственно. Аналогично, прямые ВО и ВН образуют равные углы со сторонами ВС и ВА, а прямые СО и СН – со сторонами СВ и СА. Такие точки О и Н называют изогонально сопряженными относительно треугольника АВС.
Общее утверждение формулируется тогда следующим образом. Пусть точки Р и
Q – изогонально сопряженные относительно треугольника АВС, а треугольник АРВРСР образован основаниями перпендикуляров, опущенных из Р на прямые, содержащие стороны треугольника АВС (педальный треугольник). Тогда прямые, соединяющие вершины треугольника АВС с точкой Q, перпендикулярны соответствующим сторонам треугольника АРВРСР.4.3. На какое наибольшее количество нулей может оканчиваться произведение трех натуральных чисел, сумма которых равна 407?
Ответ
: на шесть нулей.Например, 250 + 125 + 32 = 407 и 250× 125× 32 = 56× 26 = 106 = 1000000. Докажем, что больше шести нулей быть не может.
Первый способ. Разложим искомое произведение на простые множители. Если на его конце больше шести нулей, то оно должно содержать множитель 5 не менее, чем в седьмой степени. При этом каждое из трех данных чисел может содержать множитель 5 не более, чем в третьей степени, так как 54 = 625 > 407. Причем, если два слагаемых делятся на 5, то третье слагаемое на 5 не делится, так как их сумма 407 не делится на 5. Таким образом, множитель 5 содержится не более, чем в третьей степени, и не более, чем в двух слагаемых, то есть произведение содержит его не более, чем в шестой степени.
Второй способ. Пусть а, b и с – три данных числа, тогда ![]() . Следовательно, abc < 2003 = 8000000, то есть произведение не может содержать более шести нулей.
. Следовательно, abc < 2003 = 8000000, то есть произведение не может содержать более шести нулей.
Пятый тур (15 минут; каждая задача – 7 баллов
).5.1.
Известно, что {x}× [x] = 100. Найдите [x2] – [x]2.Напомним, что
[x] (целая часть x) – наибольшее целое число, не превосходящее x; {x}× (дробная часть x) – разность между числом x и его целой частью.Ответ
: 200.Так как
x = [x] + {x}, то [x2] = [([x] + {x})2] = [[x]2 + 2[x]{x} + {x}2] = [[x]2 + 200 + {x}2]. Кроме того, число [x]2 + 200 – целое, а 0 < {x}2 <1. Следовательно, [[x]2 + 200 + {x}2] = [x]2 + 200.Таким образом,
[x2] – [x]2 = 200.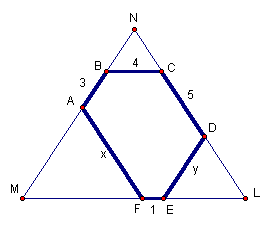
5.2.
Каждый угол шестиугольника АВСDEF равен 120° . Найдите DE и AF, если АВ = 3, ВС = 4, CD = 5 и EF = 1.Ответ
: DE = 6; AF = 8.Продолжим стороны АВ
, CD и EF до их попарного пересечения в точках M, N и L (см. рис. 7). Тогда в каждом из треугольников MAF, BNC и DLE есть по два угла, равных 60° , то есть эти треугольники равносторонние. Следовательно, треугольник MNL – также равносторонний.Пусть
AF = x; DE = y. Тогда x + 3 + 4 = 4 + 5 + y = y + 1 + x, откуда x = 8, y = 6.
5.3. Среди первых 99 натуральных чисел выбрано 50 чисел. Известно, что никакие два из них не дают в сумме ни 99, ни 100. Найдите сумму выбранных чисел.
Ответ: 3725.
Разобьем первые 99 натуральных чисел (кроме числа 50) на пары так, чтобы сумма чисел в каждой паре равнялась 100: (1; 99), (2; 98), ..., (48; 52), (49; 51).
Из условия следует, что из каждой пары могло быть выбрано только одно число, таких пар – 49, поэтому число 50 должно быть выбрано обязательно.
Тогда из последней пары не могло быть выбрано число 49 (иначе 50 + 49 = 99), то есть из нее выбрано число 51. Значит, из предпоследней пары должно было быть выбрано число 52 (иначе 48 + 51 = 99). Аналогичным рассуждением получим, что из предыдущей пары выбрано число 53, и так далее, до числа 99, выбранного из первой пары.
Таким образом, искомый набор чисел восстанавливается однозначно: 50, 51, ..., 99. Сумма чисел в таком наборе равна: 50 + 51 + ... + 99 = (50 + 99)×
25 = 149× 25 = 3725.