1.1. Найдите значение выражения , если x² + y² = 6xy и x ¹ y.

Ответ: .

Второй способ. Пусть (x ¹ 0, так как в противном случае из равенства в условии следует, что y = 0). Тогда, разделив все члены исходного равенства на x², получим, что t² – 6t + 1 = 0. Корни этого уравнения: t = 3 ± 2. Тогда = = .

1.2. При показе итогов регаты изображение вылезло за пределы квадратного экрана на 20 см (с каждой стороны). На какое наименьшее расстояние (выраженное целым количеством сантиметров) надо приблизить экран к проектору, чтобы изображение поместилось на экран полностью, если «угол зрения» проектора равен 60° ?

Ответ: на 35 см.

Посмотрев на ситуацию «в профиль», получим следующую картинку (см. рис. 1), где А – проектор, PQ и Р₁Q₁ – начальное и искомое положения экрана соответственно.

Рассмотрим прямоугольный треугольник Р₁РВ: BP = 20 см; Ð BP₁P = Ð BAC = 30° . Изображение полностью поместится на экран, если .

Оценим полученное число, исходя из условия задачи. Так как > 1,7, то 20 > 34. При этом 20 < 35, поскольку (20)² = 1200 < 35² = 1225.

1.3. Кузнечик прыгает по координатной прямой. Сначала он прыгает из точки с координатой 0 в точку с координатой 1, а длина каждого следующего прыжка вдвое больше предыдущего. Сможет ли он вернуться в исходную точку, двигаясь подобным образом? (Направление каждого прыжка: влево или вправо – не зависит от направления предыдущего прыжка.)

Ответ: нет, не сможет.

Заметим, что длины прыжков кузнечика являются последовательными степенями двойки: 1, 2, 4, 8, … . Далее можно рассуждать различными способами.

Первый способ. Поскольку длина первого прыжка нечетна, а остальные длины прыжков – четные, то и сумма длин всех прыжков нечетна. А для того, чтобы вернуться в начальную точку, кузнечику нужно преодолеть путь четной длины.

Второй способ. Заметим, что в любой момент длина последнего прыжка больше, чем сумма длин всех предыдущих прыжков: 2ⁿ > 1 + 2 + 2² + … + 2ⁿ – 1 = 2ⁿ – 1. Это означает, что после n – 1 прыжков кузнечик не может оказаться от начала координат на расстоянии 2ⁿ.

2.1. Решите систему уравнений: .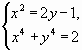

Ответ: (1; 1); (- 1; 1).

Û . Так как y = 1 является одним из решений последнего уравнения, то, разделив многочлен в левой части этого уравнения на (y – 1), получим уравнение: y³ + y² + 5y + 1 = 0. При y ³ 0,5 левая часть полученного уравнения принимает только положительные значения, поэтому других корней, удовлетворяющих данной системе уравнений, оно не имеет. Если y = 1, то x⁴ = 1 Û x = ± 1.

2.2. Найдите наибольший периметр параллелограмма, диагонали которого 6 см и 8 см.

Ответ: 20 см.

Докажем, что среди всех параллелограммов с данными длинами диагоналей наибольший периметр имеет ромб.

Действительно, пусть a и b – длины соседних сторон параллелограмма, а и – длины его диагоналей (см. рис. 2). Тогда периметр параллелограмма: P = 2(a + b).

Из равенства , выражающего теорему о сумме квадратов диагоналей параллелограмма, следует, что у всех параллелограммов с данными диагоналями сумма квадратов сторон есть величина постоянная.

По неравенству между средним арифметическим и средним квадратичным: Û , причем равенство достигается т. и т. т., когда a = b. Значит, параллелограмм с наибольшим периметром является ромбом.

Находим сторону этого ромба: = 5 (см).

Отметим, что вместо теоремы о сумме квадратов диагоналей параллелограмма можно было дважды использовать теорему косинусов (например, для треугольников АОВ и BОC), выразив стороны а и b через длины диагоналей и угол j между диагоналями (см. рис. 2). Далее используется то же самое неравенство.

2.3. В футбольном турнире участвовало 5 команд. Каждая команда сыграла с каждой по одному разу (выигрыш – 3 очка, ничья – 1 очко, проигрыш – 0). Все участники, кроме победителя, набрали очков поровну. Каков наименьший возможный отрыв команды-победителя?

Ответ: 1 очко.

Меньшим, чем 1 очко, разрыв быть не может. Приведем пример турнирной таблицы, удовлетворяющей условию, где требуемый разрыв составляет 1 очко:

 

 

 

 

 

 

 

Третий тур (20 минут; каждая задача – 8 баллов).

3.1. Изобразите такой график функции, определенной на отрезке [–4; 4], что при повороте на 90° с центром в начале координат он переходит в себя.

Ответ: см., например, рис. 3.

 

3.2. Биссектрисы углов треугольника АВС пересекают стороны ВС, СА и АВ в точках P, Q и R соответственно. Р₁ – точка пересечения прямой, проходящей через точку Р параллельно АВ, со стороной СА. Аналогично определяются точки Q₁ и R₁. Найдите сумму , если длины сторон исходного треугольника равны а, b и с.

Ответ: .

Из подобия треугольников АВС и следует, что , то есть (см. рис. 4).

Выразим PC через стороны треугольника АВС. Для этого используем свойство биссектрисы треугольника: и равенство . Из системы уравнений получим, что . Следовательно, .

Аналогично находим, что и . Тогда искомая сумма: = .

3.3. Найдите все натуральные числа, которые можно представить в виде , где m и n – также натуральные числа.

Ответ: в указанном виде можно представить любое натуральное число.

Пусть m = n + 2, где n – некоторое натуральное число. Тогда = = = . Следовательно, для требуемого представления произвольного натурального числа x достаточно, чтобы x = . Тогда при n = 2x – 1, m = 2x + 1 получим, что = x.

Отметим, что для некоторых натуральных чисел возможны и другие способы представления, например: 1 = .

4.1. Пусть a_n – целое число, ближайшее к . Найдите все такие натуральные n, что .

Ответ: n = 1056.

Первый способ. Обратим внимание на следующую закономерность:

1) , то есть ,

2) , то есть , и так далее.

Докажем указанную закономерность, обосновав ее сначала для уже рассмотренных частных случаев:

1) , поскольку , а .

2) , поскольку , а .

В общем виде: докажем, что для любых натуральных n .

Поскольку , то достаточно показать, что выполняется система неравенств: . Раскрывая модули и преобразуя, получим равносильную систему неравенств: Û Неравенства в последней системе – очевидны, поэтому утверждение доказано.

Таким образом, если последовательно брать группы из двух, четырех, шести и так далее дробей, то сумма дробей в каждой группе будет равна 2. Значит, для получения суммы, равной 64, необходимо взять 32 группы, то есть 2 + 4 + 6 + ... + 64 = 33× 32 = 1056 слагаемых.

Второй способ. Рассмотрим несколько первых членов натурального ряда и заметим, что в этом ряду между квадратами числами m² и (m + 1)² стоит ровно 2m чисел. Действительно, (m + 1)² – m² = 2m + 1.

Для первых m чисел этого промежутка a_n = m, а для следующих m чисел a_n = m + 1. Действительно, m² + m = (m + 0,5)² – 0.25, то есть , а m² + m + 1 = (m + 0,5)² + 0.75, то есть .

Разобьем теперь натуральный ряд на интервалы постоянства и найдем их длины. Слева от числа вида (m + 1)² будет m чисел, для которых a_n = m + 1, а справа будет m + 1 таких чисел. Всего чисел, для которых a_n = m + 1, будет m + 1 + (m + 1) = 2(m + 1). Следовательно, сумма обратных величин для этих чисел равна = 2.

По условию, сумма чисел в первых k интервалах равна 64, следовательно, k = 32. Искомое число n соответствует последнему числу последнего интервала, то есть n = k² + k = k(k + 1) = 32× 33 = 1056.

Поскольку при увеличении количества членов их сумма увеличивается, то найденное решение – единственное.

4.2. На гипотенузе АВ равнобедренного прямоугольного треугольника АВС отмечены точки М и N так, что угол МСN равен 45° (точка M лежит между А и N). Докажите, что АМ² + BN² = MN².

Первый способ. Мысленно «перегнем чертеж» по лучам CM и СN и докажем, что в этом случае точки А и В «попадут» в одну и ту же точку D (см. рис. 5а).

Действительно, Ð ACM + Ð BCN = 45° = Ð MCN, то есть лучи СА и СВ при перегибании совпадают, и СA = CD = СB.

Следовательно, Ð MDN = Ð MDC + Ð NDC = Ð MAC + Ð NBC = 90° . Из прямоугольного треугольника MDN по теореме Пифагора получим: .

Второй способ. Достроим треугольник АВС до квадрата KАCB, обозначив точки пересечения лучей СМ и CN со сторонами квадрата через Р и Q (см. рис. 5б). Докажем, что точка С является центром вневписанной окружности треугольника PKQ, касающейся стороны PQ.

Действительно, выполняются два условия: 1) точка С лежит на биссектрисе угла PKQ; 2) угол между биссектрисами внешних углов P и Q треугольника PKQ равен: = = 45° = Ð PCQ.

Проведем перпендикуляр CD к отрезку PQ, являющийся радиусом вневписанной окружности (наряду с отрезками СА и СВ). Так как CA = CD = CB, то D САР = D СDР и D СBQ = D СDQ (в обоих случаях прямоугольные треугольники равны по катету и гипотенузе). Следовательно, DM = AM и DN = BN. Кроме того, Ð MDC = Ð MAC = 45° и Ð NDC = Ð NBC = 45° . Таким образом, треугольник MDN – прямоугольный, откуда и следует требуемое утверждение.

4.3. Дано 51 различное натуральное число, меньшее 100. Докажите, что из них можно выбрать шесть таких чисел, что никакие два из выбранных не имеют одинаковых цифр ни в одном разряде.

По принципу Дирихле в первой сотне чисел найдется десяток, в который попадет хотя бы шесть из данных чисел. Останется не менее 41 числа, поэтому среди других десятков найдется тот, в который попало не менее пяти из данных чисел. Рассуждая аналогичным образом, получим, что еще есть десяток, в который попало не менее четырех данных чисел, еще есть десяток, в который попало не менее трех чисел, еще есть десяток, содержащий хотя бы два и еще есть десяток, содержащий хотя бы одно из данных чисел. Таких десятков, которые мы назовем «отмеченными», получается не менее шести.

У чисел внутри одного десятка в разряде единиц стоят различные цифры, поэтому искомый набор чисел можно получить так: берем число из последнего «отмеченного» десятка, затем берем число из предпоследнего «отмеченного» десятка с другой цифрой единиц и так далее. Выбранные шесть чисел не могут иметь одинаковых цифр ни в одном разряде.

5.1. Числа а, b, x и y удовлетворяют равенствам: (a + b)(x + y) = 1 и (a² + b²)(x² + y²) = 1. Докажите, что ax + by ³ 0.

Первый способ («алгебраический»). Перепишем условие задачи в виде: Û Из второго равенства следует, что Û , тогда из первого равенства: ax + by = 1 – (bx + ay) ³ 0, что и требовалось доказать.

Второй способ («векторный»). Из первого равенства в условии следует, что ax + by = 1 – (bx + ay), поэтому достаточно доказать, что bx + ay £ 1.

Пусть в декартовой системе координат (b; a), (x; y). Тогда , . Из второго равенства в условии получим, что = 1. Следовательно, bx + ay = = £ 1, что и требовалось.

Третий способ («тригонометрический»). Рассмотрим точки M(a; b) и N(x; y) в декартовой системе координат (см. рис. 6). Из первого равенства в условии следует, что ни одна из выбранных точек не совпадает с началом координат. Пусть , . Тогда , и , , где a и b – углы, которые образуют с координатным лучом Ox лучи ОM и ON соответственно. Тогда . При этом требуется доказать, что .

Из второго уравнения системы получим, что , тогда = . Следовательно, . Таким образом, , что и требовалось.

Отметим, что этот способ решения фактически использует полярную систему координат.

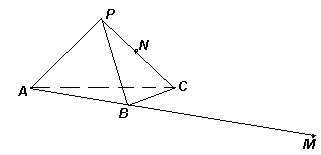
5.2. На столе стоит правильная треугольная пирамида РАВС (сделанная из стекла), все ребра которой равны 1 (см. рис.). Муравей ползет из точки М, лежащей на луче АВ на расстоянии 2 от точки В, в точку N – середину ребра РС. Найдите длину его кратчайшего пути.

Ответ: .

Рассмотрим произвольный путь муравья из точки М в точку N по столу и по грани РВС пирамиды (см. рис. 7). Этот маршрут должен пройти через некоторую точку Q ребра ВС.

Пусть К – середина отрезка АС, тогда QN = QK (соответствующие отрезки в равных треугольниках РВС и АВС). Поэтому расстояние, пройденное муравьем, равно: MQ + QN = MQ + QK ³ MK (неравенство треугольника). Равенство достигается тогда и только тогда, когда точка Q совпадает с точкой R пересечения MK и BC.

Таким образом, длина кратчайшего пути муравья равна длине отрезка MK, которую можно вычислить, например, по теореме косинусов из треугольника АМК: = ; MK = .

5.3. Найдите все целые решения уравнения k(k + 1) = n³.

Ответ: k = –1, n = 0 или k = 0, n = 1.

Докажем, что каждое из чисел k и k + 1 является кубом целого числа. Действительно, пусть p – произвольный простой делитель числа n, тогда в разложение числа n³ на простые множители он входит с показателем степени a , кратным трем. Последовательные целые числа k и k + 1 являются взаимно простыми, то есть pa целиком содержится либо в разложении на простые множители числа k, либо в аналогичном разложении числа k + 1. Следовательно, каждое из рассматриваемых чисел является произведением простых множителей с показателями степеней, делящимися на 3. Таким образом, каждое из чисел k и k + 1 является кубом целого числа.

Существует только две пары кубов целых чисел, отличающихся на 1: (–1; 0) и (0; 1).