11 класс
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Пусть 0 < x < ![]() и 0 < y <
и 0 < y < ![]() . Докажите, что xcosx + ycosy <=
ycosx + xcosy.
. Докажите, что xcosx + ycosy <=
ycosx + xcosy.
Преобразуем разность левой и правой части доказываемого неравенства: xcosx + ycosy – ycosx – xcosy = (x – y)(cosx – cosy).
Функция f(t) = cost убывает на ![]() , следовательно, если x ³
y, то cosx <=
cosy. Аналогично, если x <=
y, то cosx ³
cosy. Таким образом, (x – y)(cosx – cosy) <=
0 при всех указанных значениях x и y.
, следовательно, если x ³
y, то cosx <=
cosy. Аналогично, если x <=
y, то cosx ³
cosy. Таким образом, (x – y)(cosx – cosy) <=
0 при всех указанных значениях x и y.
Следовательно, xcosx + ycosy <= ycosx + xcosy, что и требовалось доказать.
1.2. Из отрезков с длинами 1, 1, 1, ![]() ,
, ![]() ,
, ![]() составили тетраэдр. Какое наибольшее количество граней может оказаться прямоугольными треугольниками?
составили тетраэдр. Какое наибольшее количество граней может оказаться прямоугольными треугольниками?
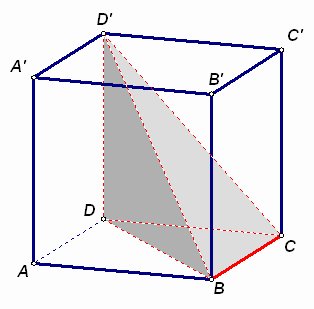
Ответ: все четыре грани.
Рассмотрим куб ![]() с ребром 1 (см. рис. 1а). Так как диагональ единичного квадрата равна
с ребром 1 (см. рис. 1а). Так как диагональ единичного квадрата равна ![]() , а диагональ единичного куба равна
, а диагональ единичного куба равна ![]() , то
, то ![]() – один из тетраэдров, которые можно составить из отрезков, указанных в условии. Очевидно, что все его грани – прямоугольные треугольники.
– один из тетраэдров, которые можно составить из отрезков, указанных в условии. Очевидно, что все его грани – прямоугольные треугольники.
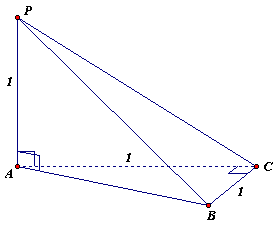
Такой тетраэдр можно составить и не используя куб. Например, рассмотрим равнобедренный прямоугольный треугольник АВС с катетами АС = ВС = 1 и восстановим перпендикуляр АР к плоскости этого треугольника длины 1 (см. рис. 1б). По определению прямой, перпендикулярной плоскости, РА^
АВ и РА^
АС Проведя отрезки РВ и РС, получим: РС = АВ =![]() , РВ =
, РВ = ![]() (угол РСВ – прямой по теореме о трех перпендикулярах).
(угол РСВ – прямой по теореме о трех перпендикулярах).
1.3. Пусть А – произведение всех простых чисел, не превосходящих 2008, B – произведение всех нечетных чисел, не превосходящих 2008. Найдите предпоследнюю цифру в десятичной записи числа А× B.
Ответ: 5.
Рассмотрим указанное произведение простых чисел. Поскольку в него входят множители 2 и 5, то оно оканчивается на ноль. Так как все остальные множители нечетные, то предпоследняя цифра числа А – нечетная.
Произведение нечетных чисел оканчивается на 5 (поскольку один из множителей равен пяти, а остальные – нечетные). Перемножая числа А = ![]() и В =
и В = ![]() , где а – нечетная цифра, получим число вида
, где а – нечетная цифра, получим число вида ![]() .
.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Существует ли многочлен Р(x) ненулевой степени с целыми коэффициентами такой, что ![]() = 2008?
= 2008?
Ответ: да, существует.
Построить пример можно из следующих соображений. Сначала найдем многочлен ![]() ненулевой степени с целыми коэффициентами, для которого число
ненулевой степени с целыми коэффициентами, для которого число ![]() является корнем. Пусть
является корнем. Пусть ![]() , тогда
, тогда ![]() Þ
Þ
![]() Û
Û
![]() . Таким образом,
. Таким образом, ![]() . (Этот же квадратный трехчлен получится, если в качестве второго корня выбрать число
. (Этот же квадратный трехчлен получится, если в качестве второго корня выбрать число ![]() и воспользоваться теоремой Виета.)
и воспользоваться теоремой Виета.)
Если ![]() , то
, то ![]() + 2008 = 2008, откуда следует, что многочлен
+ 2008 = 2008, откуда следует, что многочлен ![]() удовлетворяет условию задачи.
удовлетворяет условию задачи.
2.2. Точка Е лежит на диагонали АС трапеции АВСD. Найдите отношение ее оснований ВС и AD, если площадь треугольника ADE в два раза больше площади треугольника АВЕ.
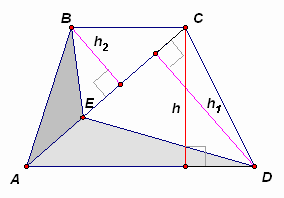
Ответ: ![]()
Пусть h1 и h2 – перпендикуляры, опущенные на диагональ АС из вершин D и В соответственно, а h – высота трапеции (см. рис. 2). Тогда 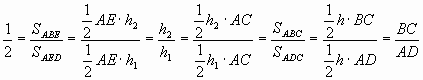 .
.
2.3. Можно ли расставить в вершинах правильного 45-угольника цифры 0, 1, ¼ , 9 так, чтобы для любой пары различных цифр нашлась сторона, концы которой занумерованы этими цифрами?
Ответ: нет, нельзя.
Всего из цифр 0, 1, …, 9 можно составить 45 различных пар (пары (a, b) и (b, a) считаются одинаковыми). Поэтому каждая пара должна встретиться ровно один раз на концах стороны 45-угольника. Заметим, что цифра, стоящая в каждой вершине, участвует ровно в двух парах, поэтому каждая цифра окажется на концах у четного числа сторон многоугольника. Но всего пар, в которых участвует конкретная цифра, – девять. Полученное противоречие доказывает, что расставить цифры требуемым образом нельзя.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Известно, что а ³ b ³ c ³ d ³ 0 и a + b + c + d = 1. Найдите наименьшее значение выражения 7a2 + 5b2 + 3c2 + d2.
Ответ: 1.
Значение 1 достигается при a = b = c = d = ![]() . Докажем, что при заданных условиях 7a2 + 5b2 + 3c2 + d2 ³
1.
. Докажем, что при заданных условиях 7a2 + 5b2 + 3c2 + d2 ³
1.
Первый способ («алгебраический»). Так как a + b + c + d = 1, то (a + b + c + d)2 = 1 Û a2 + b2 + c2 + d2 + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd = 1.
Так как а ³ b ³ c ³ d ³ 0, то выполняются неравенства: 2a2 ³ 2ab, 2a2 ³ 2aс, 2a2 ³ 2ad, 2b2 ³ 2bc, 2b2 ³ 2bd и 2c2 ³ 2cd.
Заменив в полученном равенстве удвоенные произведения на соответствующие удвоенные квадраты, получим требуемое неравенство.
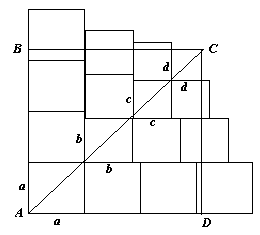
Второй способ («геометрический»). Рассмотрим квадрат АВСD со стороной 1 (см. рис. 3). Разместим в его левом нижнем углу квадрат со стороной а. Из условия следует, что ![]() , поэтому, если разместить еще три таких же квадрата «в столбик» и еще три – «в строчку», то мы либо «вылезем» за границы АВСD, либо (при
, поэтому, если разместить еще три таких же квадрата «в столбик» и еще три – «в строчку», то мы либо «вылезем» за границы АВСD, либо (при ![]() ) «попадем» на стороны ВС и CD.
) «попадем» на стороны ВС и CD.
Аналогичным образом разместим квадрат со стороной b в нижнем углу оставшегося квадрата, и добавим по два таких же квадрата «в столбик» и «в строчку». Так как ![]() , то и в этом случае незаполненным останется только квадрат со стороной 1 – (а + b). Заполнив его описанным образом тремя квадратами со стороной
, то и в этом случае незаполненным останется только квадрат со стороной 1 – (а + b). Заполнив его описанным образом тремя квадратами со стороной ![]() , мы получим незаполненным только один квадрат со стороной d. Сумма площадей шестнадцати построенных квадратов равна левой части доказываемого неравенства.
, мы получим незаполненным только один квадрат со стороной d. Сумма площадей шестнадцати построенных квадратов равна левой части доказываемого неравенства.
Отметим, что если среди чисел а, b, c и d есть хотя бы два различных, то доказанное неравенство обращается в строгое.
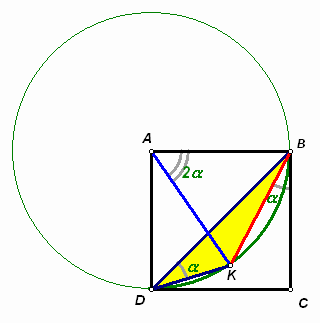
3.2. Внутри квадрата АВСD выбрана точка K такая, что Ð KBC = Ð KDB = a . Найдите угол KAD.
Ответ: Ð KAD = 90° – 2a .
Из условия задачи следует, что точка K лежит внутри треугольника BСD и что a < 45° (см. рис. 4 а, б). Действительно, если это не так, то Ð BDK < 45° , а Ð KBC > 45° , что противоречит условию.
Заметим, что Ð DKB = 180° – (Ð BDK + Ð DBK) = 180° – (a + (45° – a )) = 135° . Далее можно рассуждать по-разному.
Первый способ. Проведем окружность с центром А, проходящую через точки В и D (см. рис. 4а). Так как ![]() , то точка K лежит на этой окружности.
, то точка K лежит на этой окружности.
Тогда Ð KAD = 90° – Ð KAB = 90° – 2Ð KDB = 90° – 2a , так как угол KAB – центральный, а угол KDB – вписанный, опирающийся на ту же дугу АВ.
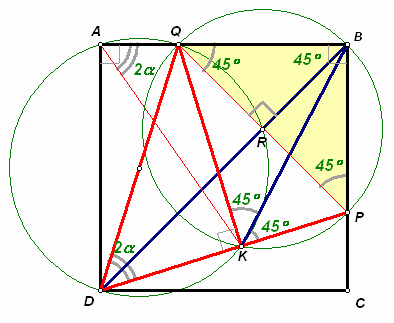
Второй способ. Отметим точку Р пересечения прямой DK со стороной квадрата ВС (см. рис. 4б). Проведем также перпендикуляр KQ к отрезку DK (Q – точка его пересечения со стороной АВ).
Докажем, что точки Р и Q симметричны относительно прямой BD. Действительно, так как Ð СВA = Ð QKP = 90° , то около четырехугольника KQBP можно описать окружность (с диаметром QP).
Так как Ð DKB = 135° , то Ð QKB = Ð BKP = 45° . По свойству углов, вписанных в окружность, получим: Ð QPB = Ð QKB = 45° и Ð ВQP = Ð BKP = 45° . Следовательно, BP = BQ, значит BD – серединный перпендикуляр к отрезку PQ.
Тогда отрезки DP и DQ также симметричны относительно прямой BD, поэтому Ð PDQ = 2a . Так как Ð DАВ = Ð DKQ = 90° , то около четырехугольника DAQK также можно описать окружность (с диаметром DQ).
Следовательно, Ð KAQ = Ð PDQ = 2a , то есть Ð KAD = 90° – 2a .
3.3. Докажите, что среди любых 39 последовательных натуральных чисел обязательно найдется число, у которого сумма цифр делится на 11.
Выберем произвольно 39 последовательных натуральных чисел. Среди них обязательно найдутся три полных десятка (в каждый десяток входят числа ![]() ,
, ![]() , ...,
, ..., ![]() ). Среди этих десятков найдутся два соседних десятка, у которых одинаковая цифра в разряде сотен. Рассмотрим эти двадцать чисел. Пусть сумма цифр первого из них равна S. Так как оно оканчивается на ноль, то суммы цифр следующих чисел последовательно равны: S + 1, S + 2, …, S + 9, S + 1 (первое число второго десятка), S + 2, …, S + 10. Среди одиннадцати натуральных чисел S, S + 1, ..., S + 10 обязательно найдется число, кратное 11.
). Среди этих десятков найдутся два соседних десятка, у которых одинаковая цифра в разряде сотен. Рассмотрим эти двадцать чисел. Пусть сумма цифр первого из них равна S. Так как оно оканчивается на ноль, то суммы цифр следующих чисел последовательно равны: S + 1, S + 2, …, S + 9, S + 1 (первое число второго десятка), S + 2, …, S + 10. Среди одиннадцати натуральных чисел S, S + 1, ..., S + 10 обязательно найдется число, кратное 11.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. При каких b найдутся такие a, что система уравнений 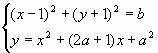 имеет хотя бы одно решение?
имеет хотя бы одно решение?
Ответ: при b ³ 2.
Первое уравнение системы имеет решения при b ³
0. Его графиком является окружность с центром (1; –1) и радиусом ![]() (при b = 0 она «вырождается» в точку).
(при b = 0 она «вырождается» в точку).
Графиком второго уравнения является парабола, «ветви» которой направлены вверх. Докажем, что для любой точки полуплоскости, задаваемой неравенством y ³ x, найдется значение а, при котором соответствующая парабола пройдет через эту точку. Это можно сделать различными способами.
Первый способ. Перепишем второе уравнение системы в виде: y – x = (x + a)2. Тогда неравенство y – x ³
0 Û
y ³
x является необходимым условием существования такого а. Оно же является достаточным, поскольку при фиксированном x выражение (x + a)2 может принимать любое неотрицательное значение. Таким образом, объединение графиков уравнений ![]() при всех значениях а есть полуплоскость y ³
x.
при всех значениях а есть полуплоскость y ³
x.
Второй способ. Рассмотрим уравнение параболы как квадратное относительно переменной а: ![]() . Его упрощенный дискриминант:
. Его упрощенный дискриминант: ![]() . Для того, чтобы указанное значение а существовало, необходимо и достаточно, чтобы квадратное уравнение имело корни, то есть чтобы выполнялось неравенство
. Для того, чтобы указанное значение а существовало, необходимо и достаточно, чтобы квадратное уравнение имело корни, то есть чтобы выполнялось неравенство ![]() . Таким образом, множество всех точек плоскости, через которые проходит хотя бы одна из парабол вида
. Таким образом, множество всех точек плоскости, через которые проходит хотя бы одна из парабол вида ![]() , является «верхней» полуплоскостью с границей y = x (включая эту границу).
, является «верхней» полуплоскостью с границей y = x (включая эту границу).
Третий способ. Вершины рассматриваемого «семейства» парабол имеют координаты: ![]() ;
; ![]() .
.
Так как y0 – x0 = ![]() , то эти вершины лежат на прямой
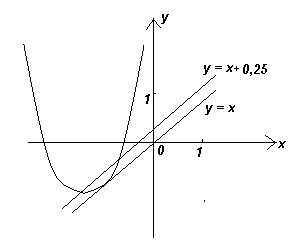
, то эти вершины лежат на прямой ![]() . Для любой из этих парабол прямая
. Для любой из этих парабол прямая ![]() является секущей, проходящей через ее вершину (см. рис. 5). Найдем уравнение касательной к произвольной параболе «семейства»
является секущей, проходящей через ее вершину (см. рис. 5). Найдем уравнение касательной к произвольной параболе «семейства» ![]() , параллельной прямой
, параллельной прямой ![]() . Оно должно иметь вид
. Оно должно иметь вид ![]() , где x0 – абсцисса точки касания. Так как искомая касательная параллельна прямой
, где x0 – абсцисса точки касания. Так как искомая касательная параллельна прямой ![]() , то
, то ![]() , то есть
, то есть ![]() . Тогда
. Тогда ![]() , а искомое уравнение имеет вид:
, а искомое уравнение имеет вид: ![]() Û
y = x.
Û
y = x.
Отсутствие параметра а в этом уравнении доказывает, что полученная прямая является общей касательной для всех парабол «семейства». По мере движения вершины параболы по прямой ![]() точки этих парабол «заметают» верхнюю полуплоскость, границей которой является найденная касательная (включая саму границу).
точки этих парабол «заметают» верхнюю полуплоскость, границей которой является найденная касательная (включая саму границу).
Отметим, что возможна некоторая разновидность этого способа решения, не использующая производную. Выберем произвольную параболу из полученного «семейства» и касательную к ней, параллельную указанной секущей. Любая парабола «семейства» получается из выбранной параллельным переносом вдоль секущей. При этом переносе рассматриваемая касательная переходит в себя и является касательной к образу выбранной параболы, так как образ пересечения равен пересечению образов. Следовательно, все параболы «семейства» имеют общую касательную.
Найдем уравнение этой касательной. Пусть ![]() , тогда уравнение параболы:
, тогда уравнение параболы: ![]() , а уравнение искомой касательной имеет вид:
, а уравнение искомой касательной имеет вид: ![]() . Система уравнений
. Система уравнений 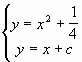 должна иметь единственное решение. Это равносильно тому, что уравнение
должна иметь единственное решение. Это равносильно тому, что уравнение ![]() имеет единственный корень. Так как полученное уравнение равносильно уравнению
имеет единственный корень. Так как полученное уравнение равносильно уравнению ![]() , то оно имеет единственный корень при с = 0. Тогда искомое уравнение касательной: y = x.
, то оно имеет единственный корень при с = 0. Тогда искомое уравнение касательной: y = x.
Найдем теперь, при каких значениях b имеет решения исходная система уравнений. Из сказанного выше следует, что это выполняется тогда и только тогда, когда окружность ![]() имеет хотя бы одну общую точку с прямой y = x. Рассмотрим систему уравнений
имеет хотя бы одну общую точку с прямой y = x. Рассмотрим систему уравнений 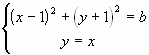 . Она имеет решения тогда и только тогда, когда имеет решения уравнение
. Она имеет решения тогда и только тогда, когда имеет решения уравнение ![]() , равносильное уравнению 2x2 = b – 2. Последнее уравнение имеет решения при b ³
2.
, равносильное уравнению 2x2 = b – 2. Последнее уравнение имеет решения при b ³
2.
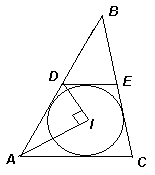
4.2. В треугольнике ABC: I – центр вписанной окружности, D – середина AB. Найдите ![]() , если известно, что угол AID – прямой.
, если известно, что угол AID – прямой.
Ответ: ![]() = 3.
= 3.
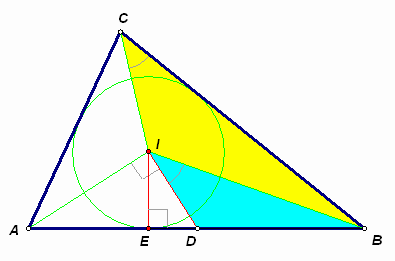
Первый способ. Проведем из точки D касательную к окружности, вписанной в треугольник АВС (см. рис. 6а). Пусть Е – точка ее пересечения со стороной ВС. Так как лучи AI и DI являются биссектрисами углов А и D четырехугольника ADEC и Ð DAI + Ð ADI = 90° , то Ð CAD + Ð ADE = 180° . Следовательно, DE || AC, то есть DE – средняя линия треугольника АВС.
По свойству описанного четырехугольника АС + DE = AD + CE, тогда 1,5АС = 0,5АВ + 0,5ВС Û
![]() = 3.
= 3.
Следующие два способа решения используют тот факт, что ![]() (так как угол AIB образован биссектрисами углов А и В треугольника АВС). Тогда, из условия задачи следует, что
(так как угол AIB образован биссектрисами углов А и В треугольника АВС). Тогда, из условия задачи следует, что ![]() (см. рис. 6 б, в).
(см. рис. 6 б, в).
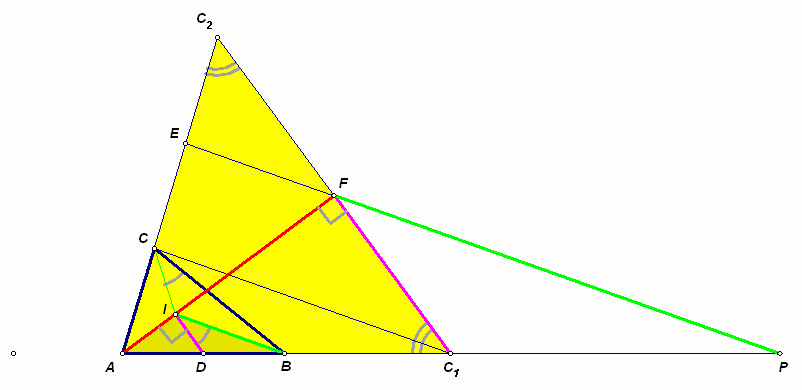
Второй способ. На луче АВ отметим точку С1 так, что ВС = ВС1 (см. рис. 6б). Через С1 проведем прямую, параллельную прямой ID, и отметим точку С2 ее пересечения с лучом АС и точку F ее пересечения с лучом AI. Тогда Ð АFC1 = 90° .
Кроме того, угол АВС – внешний угол при вершине равнобедренного треугольника СВС1, BI – его биссектриса, следовательно, BI || С1C. Тогда ![]() (углы, стороны которых противоположно направлены). Следовательно, в треугольнике АС1С2:
(углы, стороны которых противоположно направлены). Следовательно, в треугольнике АС1С2: ![]() , то есть этот треугольник – равнобедренный:
, то есть этот треугольник – равнобедренный: ![]() .
.
Следовательно, F – середина С1С2. Через точку F проведем прямую, параллельную СС1, Р и Е – точки ее пересечения с прямыми АС1 и АС2 соответственно. Тогда СЕ = С2Е (по теореме Фалеса). Кроме того, так как BI || PF, то треугольники AIB и AFP – подобны. При этом, ID – медиана треугольника AIB, значит, отрезок FC1, параллельный ID, является медианой треугольника AFP. Так как АС1 = С1P, то АС = СЕ (по теореме Фалеса).
Таким образом, ![]() =
= ![]() = 3.
= 3.
Третий способ. Заметим, что треугольники IDB и СIB подобны (по двум углам, см. рис. 6в), поэтому ![]() . Следовательно,
. Следовательно, ![]() .
.
![]() Введем стандартные обозначения: ВС = a; AC = b; AB = c;
Введем стандартные обозначения: ВС = a; AC = b; AB = c; ![]() – полупериметр, r – радиус вписанной окружности, S – площадь треугольника АВС. Тогда
– полупериметр, r – радиус вписанной окружности, S – площадь треугольника АВС. Тогда ![]() . Учитывая, что BE = p – b, из прямоугольного треугольника BEI получим:
. Учитывая, что BE = p – b, из прямоугольного треугольника BEI получим: ![]() . Следовательно,
. Следовательно, ![]() (*).
(*).
Выразим радиус вписанной окружности, используя две формулы для вычисления площади треугольника: ![]() . Тогда
. Тогда ![]() .
.
Подставив это значение в равенство (*), получим: ![]() . Преобразуем левую часть последнего равенства:
. Преобразуем левую часть последнего равенства: ![]() =
= ![]() =
= ![]() . Тогда
. Тогда ![]() =
= ![]() Û
2(p – b) = p. Следовательно,
Û
2(p – b) = p. Следовательно, ![]() Û
3b = a + c Û
Û
3b = a + c Û
![]() .
.
Отметим, что существуют и другие «вычислительные» способы решения задачи, например, можно использовать формулу для вычисления биссектрисы треугольника по его сторонам и теорему об отношении, в котором центр вписанной окружности делит биссектрису.
4.3. Имеется набор из двадцати гирь, массы которых выражаются целым числом граммов. Известно, что если из набора удалить любое количество гирь (в том числе и ноль), то оставшиеся гири нельзя будет разложить на две чашки весов так, чтобы они уравновесились. Докажите, что общая масса набора превосходит одну тонну.
Рассмотрим два произвольных подмножества гирь (возможно, пересекающихся). Докажем, что они имеют различную массу. Действительно, если удалить их общую часть, то оставшиеся наборы (согласно условию задачи) имеют различную массу. Поэтому и исходные подмножества гирь имеют различную массу.
Множество из 20 гирь имеет 220 подмножеств. По доказанному, эти подмножества гирь имеют различные целые неотрицательные массы, поэтому масса самого тяжелого подмножества (а это и есть данный набор гирь) не меньше, чем 220 –1 граммов, что больше одной тонны (1 т = 106 г; 220 = 10242 > 106 + 1).
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Имеет ли уравнение ![]() =
= ![]() целые корни?
целые корни?
Ответ: да, имеет.
Например, x = –2009. Действительно, при x = –2009 получим: ![]() =
= ![]() =
= ![]() =
= ![]() .
.
5.2. В правильной пирамиде РАВСD расстояние от вершины Р до основания АВСD равно половине ребра АВ. Какая из вершин, В или С, находится ближе к прямой РА?
Ответ: вершины В или С равноудалены от прямой РА.
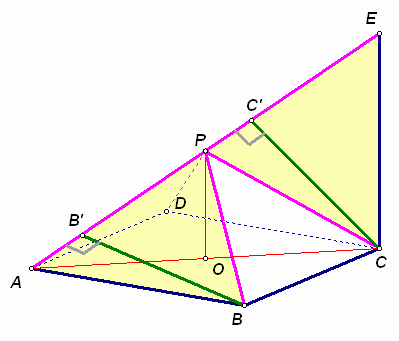
Пусть точка О – центр квадрата АВСD, тогда РО – перпендикуляр к этой плоскости (см. рис. 7а).
Первый способ. В плоскости АРС из вершины С проведем прямую, параллельную РО, которая пересечет прямую PA в некоторой точке Е. Так как ЕС || PO, то отрезок РО – средняя линия треугольника АСЕ, следовательно, АР = РЕ и ЕС = 2РО. По условию, АВ = 2РО, значит равнобедренные треугольники АРВ и СРЕ равны (по трем сторонам). Следовательно, их высоты BB’ и CC’, проведенные к боковым сторонам, также равны.
Второй способ. Проведем перпендикуляры BB’ и CC’ к прямой РА. Они являются высотами, проведенными к боковым сторонам в равнобедренных треугольниках АРВ и АРС соответственно (см. рис. 7а).
Пусть АВ = а, тогда РО = ![]() а. Из прямоугольного треугольника АОР получим, что
а. Из прямоугольного треугольника АОР получим, что 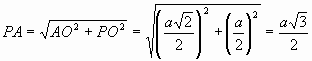 . Высота равнобедренного треугольника АРВ, проведенная к основанию АВ, равна
. Высота равнобедренного треугольника АРВ, проведенная к основанию АВ, равна 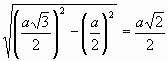 , значит
, значит ![]() . Тогда
. Тогда ![]() . Аналогично,
. Аналогично, ![]() , следовательно,
, следовательно, ![]() .
.
Отметим, что получив равенство площадей треугольников АРВ и АРС, можно было сразу сделать вывод о равенстве высот BB’ и CC’, не вычисляя их.
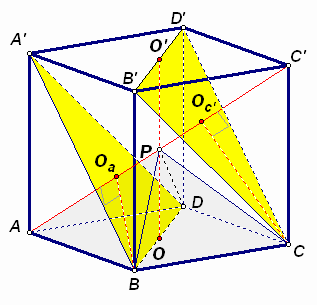
Третий способ. Так как высота пирамиды в два раза меньше ребра основания, то пирамиду можно вписать в куб АВСDA’B’C’D’ так, чтобы ее вершина Р совпала с центром куба (см. рис. 7б).
Докажем, что шесть вершин куба, не лежащих на прямой АС’ (среди них вершины В и С), расположены на равном расстоянии от этой прямой. Действительно, точки A’, B и D равноудалены от точки А, поэтому ортогональная проекция точки А на плоскость A’BD является центром Оа окружности, описанной около равностороннего треугольника A’BD. Аналогично, ортогональная проекция точки C’ на эту же плоскость также является центром окружности, описанной около треугольника A’BD, и совпадает с Оа. Следовательно, АС’^ (A’BD).
Аналогично доказывается, что АС’^ (СB’D’). Так как D A’BD = D СB’D’, то радиусы описанных окружностей этих треугольников равны.
5.3. На плоскости нарисованы красные и синие квадраты, причем множество точек, являющихся вершинами синих квадратов, совпадает со множеством точек, являющихся вершинами красных. Верно ли, что какие-то два квадрата обязательно совпадают?
Ответ: нет, не верно.
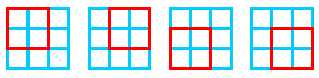
Например, девять синих квадратов (рис. 8а) и 4 красных квадрата (рис. 8б, для наглядности квадраты изображены на отдельных чертежах) имеют одно и то же множество вершин, но никакие два квадрата не совпадают.
