Ответ: (1 + a² – b²)(1 – a² + b²).

Раскроем скобки и перегруппируем: 1 + 4a²b² – (a² + b²)² = 1 + 4a²b² – a⁴ – 2a²b² – b⁴ = 1 – (a⁴ – 2a²b² + b⁴) = 1 – (a² – b²)² = (1 + a² – b²)(1 – a² + b²).

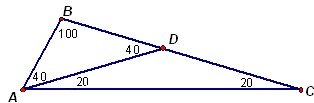
1.2. Два угла треугольника равны 100° и 60° . Покажите, как его разрезать на два равнобедренных треугольника.

Пусть в треугольнике АВС углы А и В равны 60° и 100° соответственно, тогда угол С равен 20° (см. рис. 1). Проведем отрезок AD так, чтобы Ð DAC = 20° . Тогда в каждом из треугольников ADC и ABD есть по два равных угла, то есть эти треугольники – равнобедренные.

Такой же результат можно получить из уравнения , где x – искомая разница во времени (в часах).

Первый способ. Предположим, что год не високосный. Пусть Балда x дней отработал, а (365 – x) дней прогулял, тогда по своему предложению он будет иметь право на x – (365 – x)× 10 = 11x – 365× 10 щелчков, а по предложению попа – на 12x – (365 – x)× 121 = 133x – 365× 121 щелчков.

Поскольку в итоге выяснилось, что количество щелчков в обоих случаях одно и то же, то составляем уравнение 11x – 365× 10 = 133x – 365× 121. Упростив его, получим: 122x = 365× 111. Такое уравнение не имеет натуральных решений.

Если же год високосный, то, рассуждая аналогично, получим уравнение 122x = 366× 111, то есть x = 333. Следовательно, поп должен получить от Балды 333 – (366 – 333)× 10 = 3 щелчка.

Второй способ. Пусть Балда отработал а дней и прогулял b дней, тогда a – 10b = 12a – 121b. Упрощая это равенство, получим, что 11а = 111b. Поскольку числа 11 и 111 – взаимно простые, то a кратно 111, b кратно 11. Так как а £ 366, то а может быть равно 111, 222 или 333. Соответствующие значения b: 11; 22; 33. Тогда сумма а + b (количество дней в году) принимает значения 122, 244 и 366 соответственно. Отсюда заключаем, что год был високосным, то есть а = 333, b = 33. Следовательно, попу причитается a – 10b = 333 – 330 = 3 щелчка.

Отметим, что полученный ответ полностью согласуется с литературным источником: А.С. Пушкин, «Сказка о попе и его работнике Балде».

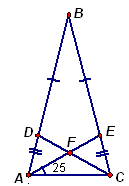
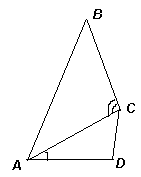
2.2. На боковых сторонах АВ и ВС равнобедренного треугольника АВС выбраны точки D и Е соответственно так, что BD = BE. Отрезки АЕ и CD пересекаются в точке F. Найдите угол AFC, если угол ЕАС равен 25° .

Так как АВ = ВС и BD = BE, то AD = CE (см. рис. 2). Кроме того, Ð ВАС = Ð ВСА (углы при основании равнобедренного треугольника). Рассмотрим треугольники ACD и CAE. Так как у них общая сторона АС, то эти треугольники равны (по двум сторонам и углу между ними). Следовательно, Ð DСA = Ð EAС = 25° . Тогда из треугольника AFC получим, что Ð АFC = 180° – (25° + 25° ) = 130° .

Пусть такое возможно, тогда выполняется равенство a² + b² = x², где a и b – простые числа. Тогда b² = x² – a² = (x – a)(x + a). Это возможно только в двух случаях: x – a = x + a = b или x – a = 1; x + a = b².

В первом случае а = 0, что противоречит условию. Во втором случае x = a + 1, тогда 2a + 1 = b², то есть 2a = (b – 1)(b + 1). Если b = 2, то a – не целое число, следовательно b – нечетное. Тогда b – 1 и b + 1 соседние четные числа, значит, одно из них кратно 2, а другое кратно 4. Следовательно, 2a делится на 8, то есть а делится на 4 – противоречие.

Пусть S – сумма всех полученных оценок, А – оценка Ани, Б – оценка Бори, В – оценка Веры. Из условия задачи следует, что: S – A = A + 10; S – Б = Б + 8; S – В = В + 6. Следовательно, S = 2A + 10 = 2Б + 8 = 2В + 6. Значит, B – Б = Б – А = 1. Так как двоек не было, то возможен только один вариант: А = 3, Б = 4, В = 5. Следовательно, S = 16, тогда S – (A + Б + В) = 4, то есть еще один ученик получил оценку «4».

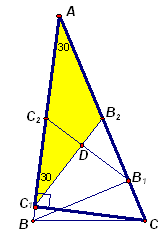
3.2. В остроугольном треугольнике ABC: Ð A = 30° ; BB₁ и CC₁ – высоты; B₂ и C₂ – середины сторон AC и AB соответственно. Под каким углом пресекаются прямые B₁С₂ и С₁B₂?

Ответ: под прямым углом.

Рассмотрим прямоугольный треугольник АВВ₁, В₁С₂ – его медиана (см. рис. 3а). По свойству прямоугольного треугольника В₁С₂ = AB = АС₂. Следовательно, треугольник АС₂В₁ – равнобедренный с углом 30° при основании, значит, Ð AС₂B₁ = 120° . Аналогично, С₁В₂ – медиана прямоугольного треугольника АCC₁ (см. рис. 3б), поэтому С₁В₂ = AС = АB₂. Следовательно, треугольник АВ₂С₁ – также равнобедренный с углом 30° при основании.

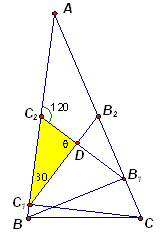
Рассмотрим треугольник С₁С₂D, где D – точка пересечения отрезков B₁С₂ и С₁B₂ (см. рис. 3в). Пусть Ð С₁DC₂ = x. По теореме о внешнем угле треугольника x + 30° = 120° . Следовательно, искомый угол между прямыми B₁С₂ и С₁B₂ равен 90° .

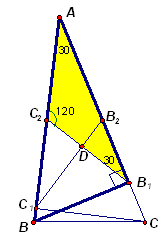
Отметим, что вместо треугольника АВ₂С₁ можно было рассмотреть треугольник В₂CC₁ (см. рис. 3б), в котором С₁В₂ = AС = СB₂ и Ð АСС₁ = 90° – Ð ВАС = 60° . Следовательно, этот треугольник – равносторонний, значит, Ð С₁B₂С = 60° . Тогда по теореме о сумме углов треугольника Ð В₁DB₂ = 90° .

3.3. В школе прошел шахматный турнир, в котором участвовало 20 шахматистов (каждый сыграл с каждым один раз). После подведения итогов оказалось, что Толя с 9,5 очками занял 19-е место, ни с кем его не разделив. Единоличным же победителем оказался Витя. Определите, сколько очков набрал каждый участник. (В шахматах за победу присуждается одно очко, за поражение – 0 очков, за ничью – пол-очка.)

Пусть a = 400, тогда первое выражение примет вид: a⁵ – (a – 1)²(a³ + 2a² + 3a + 4). Преобразуем его: a⁵ – (a – 1)²(a³ + 2a² + 3a + 4) = a⁵ – (a² – 2a + 1)(a³ + 2a² + 3a + 4) = a⁵ – a⁵ – 2a⁴ – 3a³ – 4a² + 2a⁴ + 4a³ + 6a² + 8a – a³ – 2a² – 3a – 4 = 5a – 4. Таким образом, при a = 400 значение выражения равно 1996, что меньше, чем 2000.

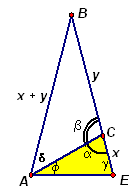
4.2. В четырехугольнике ABCD: Ð САD + Ð ВСА = 180° и АВ = ВС + АD (см. рис.). Докажите, что Ð ВАС + Ð АСD = Ð СDА.

Для удобства введем обозначения: AD = x, BC = y, Ð CAD = a , Ð ACB = b , Ð ADC = g , Ð BAC = d , Ð ACD = f (см. рис. 4а). Тогда a + b = 180° и АВ = х + у (по условию).

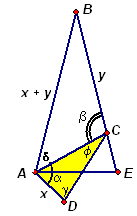
Если сумма двух углов равна 180° , то можно приложить их один к другому так, чтобы они имели общую сторону, а две другие стороны стали противоположными лучами. Поэтому «отрежем» треугольник ACD, перевернем его и приставим обратно, так чтобы вершины А и С поменялись местами. Новое положение вершины D обозначим Е.

Так как a + b = 180° , то точки В, С и Е будут лежать на одной прямой. При этом СЕ = AD = x, то есть ВЕ = х + у = AB (см. рис. 4б). В равнобедренном треугольнике АВЕ углы при основании равны, то есть d + f = g , что и требовалось.

Пусть в первом числе некоторой пары наименьшая цифра равна а, тогда во втором числе наибольшая цифра равна (10 – а). Аналогично, если в первом числе наибольшая цифра равна b, то наименьшая цифра во втором числе равна (10 – b). Тогда в каждой паре сумма двух наименьших и двух наибольших цифр равна 20. Общая сумма таких цифр будет равна 20× 364 = 7280. Добавив к этой сумме 10 (сумма наибольшей и наименьшей цифры числа 555), получим 7290.