Первый способ. Пусть a, b и c – количество пятерок, четверок и троек соответственно. Тогда: 5a + 4b + 3c = 46 и a + b + c = 10. Решая полученную систему уравнений, получим: b = 16 – 2a. Следовательно, b – четное число. Учитывая, что , осуществляем перебор:

1) Если b = 8, то а = 4, что противоречит утверждению a + b + c = 10.

2) Если b = 6, то а = 5, что также противоречит утверждению a + b + c = 10.

3) Если b = 4, то а = 6, что также противоречит утверждению a + b + c = 10.

4) Если b = 2, то а = 7, с = 1.

Второй способ Сумма всех оценок девятиклассника равна 46. Если бы девятиклассник учился на одни пятерки, то эта сумма была бы равна 50, то есть на 4 балла больше, чем в реальности. Замена оценки «5» на «3» уменьшает общую сумму на 2 балла, а замена «5» на «4» – на 1 балл.

Представим число 4 в виде суммы двоек и единиц: 4 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1. Так как все оценки у ученика присутствуют, то возможен только случай 4 = 2 + 1 + 1. Следовательно, возможен единственный набор оценок, который и приведен в ответе.

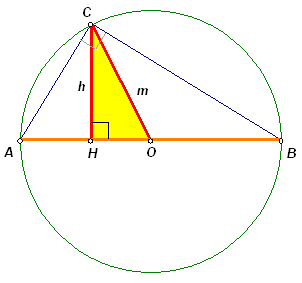
1.2. Сколько существует различных прямоугольных треугольников, у которых одна из сторон равна 5 см, а одна из высот равна 3 см?

Ответ: три.

В любом прямоугольном треугольнике две высоты совпадают с катетами, а третья высота проведена к гипотенузе.

Рассмотрим возможные варианты.

1) Если гипотенуза равна 5 см, то высотой длины 3 см может являться только один из катетов. Действительно, в прямоугольном треугольнике медиана m, проведенная из вершины прямого угла, равна половине гипотенузы, то есть 2,5 см, а высота h, проведенная к гипотенузе, не больше этой медианы (см. рис. 1).

2.1. Известно, что уравнение x⁴ + a = 0 (x – переменная, а – некоторое число) имеет два различных корня. Сколько корней имеет уравнение x⁴ + a = x²?

Уравнение x⁴ = – a имеет два различных корня тогда и только тогда, когда a < 0. В этом случае квадратное уравнение t² – t + a = 0 имеет два корня, так как D = 1 – 4a > 0. Кроме того, из теоремы Виета следует, что знаки этих корней различны. Поэтому уравнение x⁴ + a = x² равносильно уравнению x² = b, где b > 0, которое имеет два корня.

Отметим, что вместо рассуждения о корнях вспомогательного квадратного уравнения можно в одной системе координат рассмотреть графики функций y = x² и y = x⁴ + a, где a < 0. Эти графики пересекаются в двух точках (симметричных относительно оси ординат).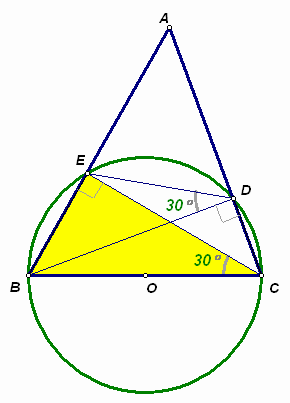

2.2. В остроугольном треугольнике АВС проведены высоты BD и CE. Найдите угол BDE, если ВС = 2ВЕ.

Так как Ð ВЕС = Ð BDС = 90° , то четырехугольник ВЕDC – вписанный (центр О описанной около него окружности – середина стороны ВС). Углы BDE и BCE – вписанные и опираются на одну и ту же дугу ВЕ, поэтому Ð BDE = Ð BCE = 30° .

Отметим, что первую часть доказательства можно было провести иначе, а именно: рассматривая все возможные остатки от деления целого числа на 6, показать, что числа n³ и n имеют одинаковые остатки при делении на 6.

Пусть a – b = m > 0, b – c = n > 0. Сложив эти равенства почленно, получим, что a – c = m + n. Перенесем в доказываемом неравенстве слагаемое с в левую часть и сделаем указанные замены. Тогда неравенство примет вид: .

Полученное неравенство верно, так как при всех x > 0 справедливо, что . Следовательно, доказываемое неравенство также верно.

Отметим, что возможны также и «лобовые» способы доказательства, но они связаны со значительными техническими трудностями.

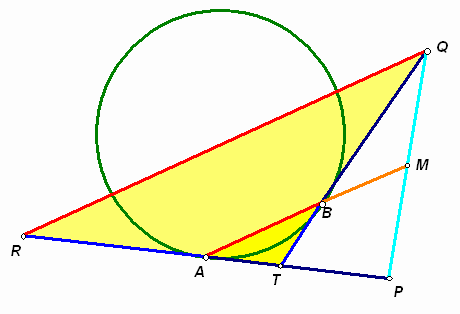
3.2. На окружности отмечены точки А и В, из которых проведены равные отрезки касательных АР и ВQ так, что АВ и РQ не параллельны. В каком отношении прямая АВ делит отрезок РQ?

Первый способ. Пусть заданные отрезки касательных расположены так, как показано на рис. 3а. Тогда Т – точка пересечения прямых АР и BQ, R – точка, симметричная точке Р относительно точки А.

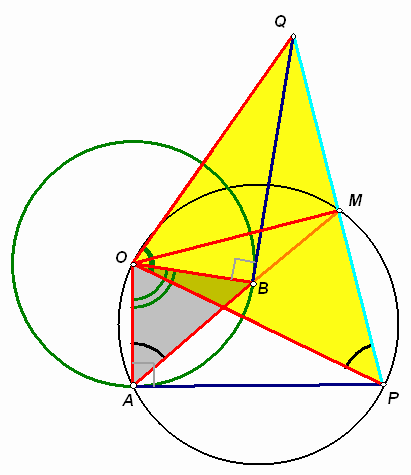
Получим, что ТА = ТВ (отрезки касательных, проведенных к окружности из одной точки), значит, RT = RA + AT = PA + BT = QB + BT = QT. Следовательно, треугольники АТВ и RTQ – равнобедренные с общим углом при вершине, поэтому прямые АВ и RQ параллельны. Так как А – середина отрезка RP, то (по теореме Фалеса) прямая АВ пересекает отрезок PQ в его середине.

Второй способ. Пусть прямая АВ пересекает отрезок PQ в точке М, О – центр данной окружности, тогда радиусы ОА и ОВ перпендикулярны касательным АР и BQ соответственно (см. рис. 3б). Прямоугольные треугольники ОАР и ОВQ равны (по двум катетам), следовательно, ОР = OQ и Ð АОР = Ð BОQ. Тогда Ð АОB = Ð PОQ, то есть в равнобедренных треугольниках АОB и PОQ равны углы при вершинах, следовательно, в этих треугольниках равны углы при основаниях. Из того, что Ð ОАB = Ð ОPQ, следует, что четырехугольник ОАРМ – вписанный, тогда Ð ОАP + Ð ОMP = 180° , значит, Ð ОMP = 90° .

Таким образом, ОМ – высота равнобедренного треугольника POQ, проведенная к основанию, поэтому ОМ – медиана этого треугольника, то есть М – середина РQ.

Пусть по итогам турнира каждая из n команд набрала m очков, то есть всего было набрано mn очков. В турнире было проведено матчей, в которых было разыграно не более, чем очков. Следовательно, , то есть .

Пусть m = 3k + p, где k – количество побед, р – количество ничьих. Тогда . Так как m фиксировано и p = m – 3k, то различных наборов вида (k; p) не больше, чем . При этом, крайние случаи (соответствующие k = 0 и ) не могут реализовываться одновременно, то есть указанных наборов меньше, чем . Тогда, по принципу Дирихле, найдутся хотя бы три команды, имеющие одинаковый набор из побед и ничьих.

4.1. Стороны а, b и c треугольника связаны соотношением a⁸ + b⁸ + c⁸ = 2a⁴b⁴ + 2b⁴c⁴ + 2c⁴a⁴. Определите вид треугольника (по углам).

Преобразуем исходное равенство: a⁸ + b⁸ + c⁸ + 2a⁴b⁴ – 2b⁴c⁴ – 2c⁴a⁴ = 4a⁴b⁴ Û (a⁴ + b⁴ – c⁴)² – (2a²b²)² = 0 Û (a⁴ + b⁴ + 2a²b² – c⁴)(a⁴ + b⁴ – 2a²b² – c⁴) = 0 Û ((a² + b²)²– (c²)²)((a² – b²)²– (c²)²)= 0 Û (a² + b² + c²)(a² + b² – c²)(a² – b² + c²)(a² – b² – c²) = 0.

Так как a² + b² + c² > 0, то справедливо хотя бы одно из трех равенств: a² + b² = c² или a² + c² = b² или b² + c² = a², то есть треугольник – прямоугольный.

4.2. В прямоугольный треугольник вписана окружность и к ней перпендикулярно гипотенузе проведены касательные, пересекающие гипотенузу в точках D и E. Под каким углом виден отрезок DE из вершины прямого угла?

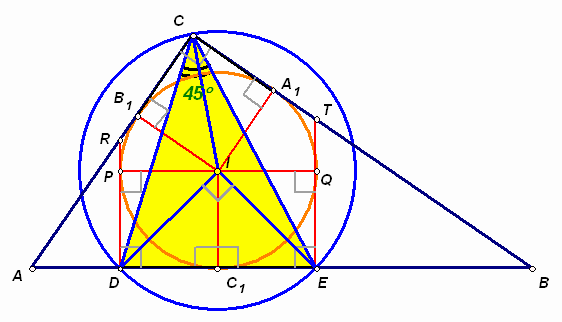
Ответ: Под углом в 45° .

Пусть АВС – данный прямоугольный треугольник (Ð С = 90° ), I – центр вписанной в него окружности, А₁, В₁ и С₁ – точки ее касания со сторонами треугольника, отрезки RD и TE – касательные к окружности (P и Q – точки касания, см. рис. 4 а, б).

Четырехугольники IB₁CA₁, IPDC₁ и IQEC₁ являются равными квадратами со стороной r, равной радиусу вписанной в треугольник окружности (из условия задачи следует, что каждый из них имеет по три прямых угла и пару смежных сторон, равных радиусу).

Далее можно рассуждать по-разному.

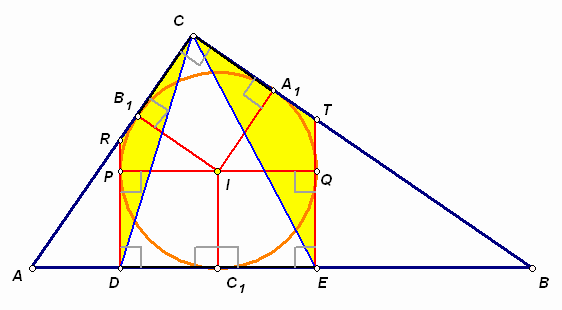
Первый способ. Точки С, D и Е находятся на одинаковом расстоянии, равном , от точки I, значит, существует окружность с центром I, содержащая эти точки (см. рис. 4а). В этой окружности прямой угол DIE – центральный, следовательно искомый угол DСE равен 45° (он вписанный и опирается на ту же дугу DE этой окружности).

Второй способ. Заметим, что треугольники DRC и ETC – равнобедренные (см. рис. 4б). Действительно, DR = DP + RP = RB₁ + B₁C = CR, аналогично, ET = CT. Тогда = . Аналогично получим, что . Таким образом, .

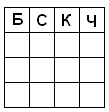
4.3. Дан квадрат 4´ 4 и четыре разных цвета. Сколькими способами можно покрасить клетки квадрата так, чтобы в каждом столбце и в каждой строке присутствовали все цвета?

Ответ: 24² = 576 способами.

Для удобства обозначим цвета: красный, синий, белый и черный. Тогда для верхней строки таблицы существует 4! = 24 способа раскраски. Для каждого из 24 способов раскраски верхней строки существует 3! = 6 способов раскраски левого столбца.

Рассмотрим один из способов раскраски верхней строки. Без ограничения общности можно считать, что клетки покрашены так, как это показано на рис. 5а.

Пусть левый столбец покрашен в таком же порядке (БСКЧ), тогда вторую строку можно покрасить тремя способами, первый из которых дает два случая (см. рис. 5 б, в), а два других однозначно определяют раскраску таблицы (см. рис. 5 г, д). Следовательно, всего существует 24× 6× (3 + 1) = 24² способов раскраски таблицы.

При любом другом способе раскраски левого столбца рассуждения аналогичны, только вместо второй строки рассматривается та строка, в которой самая левая клетка – синяя.

Пятый тур (15 минут; каждая задача – 7 баллов).

5.1. Найдите наименьшее значение выражения , если числа a и b неотрицательны и a + b = 1.

Первый способ. Рассмотрим прямоугольный треугольник АВС с катетами BС = 1 и AС = b и прямоугольный треугольник AED с катетами АD = 1 и DE = a, расположив их так, как показано на рис. 6. Тогда , . Сумма длин этих отрезков наименьшая, если точка А лежит на отрезке ВЕ, тогда искомое значение равно .

Второй способ. Пусть a = 0,5 + t; b = 0,5 – t, где 0 £ t £ 0,5. Тогда S = = + . Следовательно, S² = 2t² + 2,5 + 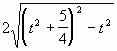= 2t² + 2,5 + . = 2t² + 2,5 + 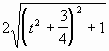. Таким образом, наименьшее значение S² достигается при t = 0 и равно 5.

Так как S > 0, то . Поскольку функция – возрастающая, то наименьшее значение S также достигается при t = 0 и равно .

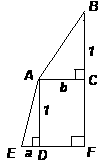
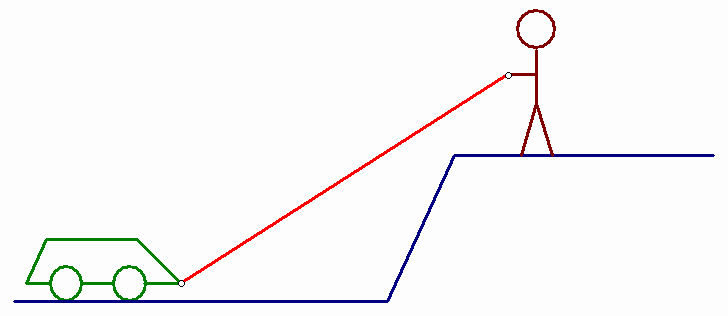
5.2. Ребенок, находящийся на мосту, тянет за веревку игрушечный автомобильчик, который катится по дороге под мостом (см. рисунок). Известно, что, «притягивая» машинку, он намотал 10 см веревки. Верно ли, что игрушка также сдвинется на 10 см? Ответ обоснуйте.

Ответ: нет, не верно.

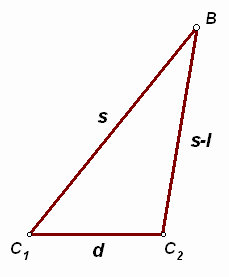
Пусть точка В – местонахождение мальчика и машинка сдвигается из точки С₁ в точку С₂ на расстояние d (см. рис. 7). Введем еще обозначения: s – начальная длина веревки, – длина, на которую мальчик намотал веревку. Тогда расстояние между мальчиком и игрушкой (после перемещения ее в точку С₂) станет равным s – l. Используя неравенство треугольника, получим: ВС₂ + С₂С₁ > BC₁, то есть d + (s – l) > s. Следовательно, d > l, значит, игрушка сдвинется на расстояние, большее, чем 10 см.

 

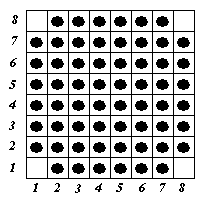
5.3. Ходом фишки, стоящей на некоторой клетке K доски 8´ 8, назовем ее прыжок на свободную клетку, которая симметрична K относительно какой-нибудь другой стоящей на доске фишки. Какое наибольшее количество фишек можно поставить на клетки этой доски так, чтобы любая фишка могла сделать ход?