10 класс
Первый тур (10 минут; каждая задача – 6 баллов).
1.1.
Решите уравнение:Ответ: корней нет.
Так как 4cosp
x £
4, а 4x2 – 4x + 5 = (2x – 1)2 + 4 ³
4, то исходное равенство достигается т. и т. т., когда его левая и правая части равны 4, то есть данное уравнение равносильно системе: ![]() . Но x =
. Но x = ![]() (решение второго уравнения) не является решением первого уравнения, поскольку
(решение второго уравнения) не является решением первого уравнения, поскольку ![]() .
.
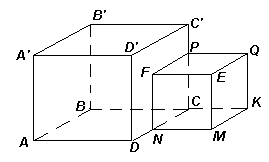
1.2. На плоскости АВС расположены два куба АВСDA’B’C’D’ и
KMNCQEFP – так, как это показано на рисунке. Сравните длины отрезков AP и D’K.Ответ: длины этих отрезков равны.
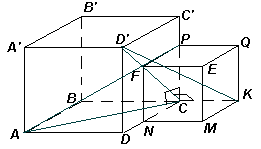
Первый способ. Рассмотрим поворот вокруг прямой
DC на 90° : образом точки А является точка D’, а образом точки Р – точка K (см. рис. 1а). Следовательно, образом отрезка AP является отрезок D’K, значит, AP = D’K.Второй способ. Рассмотрим прямоугольные треугольники АСР и D’СK (см. рис. 1а): АС = D’С (диагонали граней большего куба) и
CP = CK (ребра меньшего куба). Следовательно, D АСР = D D’СK (по двум катетам), значит, AP = D’K.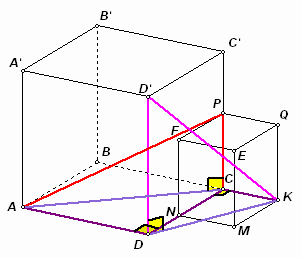
Третий способ. Пусть
a и b – длины ребер большего и меньшего кубов соответственно (см. рис. 1б). Тогда, из прямоугольных треугольников ACP и ADC, получим: AP2 = АС2 + РС2 = AD2 + DC2 + PC2 = 2a2 + b2. Аналогично, из прямоугольных треугольников KDD’ и DCK, получим: D’K2 = DK2 + D’D2 = DC2 + CK2 + D’D2 = 2a2 + b2. Следовательно, AP = D’K.
1.
3. Докажите, что сумма цифр в десятичной записи числа 3200 меньше, чем 1000.Так как 32 < 10, то 3200 < 10100. Следовательно, в десятичной записи числа 3200 не больше, чем 100 цифр. Значит, сумма цифр числа 3200 не превосходит 900, то есть она меньше 1000.
Второй тур (1
5 минут; каждая задача – 7 баллов).2.1. Известно, что а
> b > c. Докажите, чтоРассмотрим разность левой и правой частей доказываемого неравенства и преобразуем ее: ![]() =
= ![]() =
= ![]()
Эту же идею можно реализовать в другой форме: ![]()
2.2.
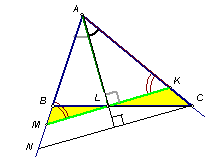
В треугольнике АВС проведена биссектриса АL. Через точку L проведена прямая, перпендикулярная AL и пересекающая лучи АВ и АС в точках М и K соответственно. Найдите AK, если АВ = 4, АС = 6.Ответ: 4,8.
Так как отрезок AL является высотой и биссектрисой треугольника AMK (см. рис. 2 а, б), то этот треугольник – равнобедренный (АМ = AK). Кроме того, из треугольника АВС (по свойству биссектрисы): ![]() . Далее можно рассуждать по-разному.
. Далее можно рассуждать по-разному.
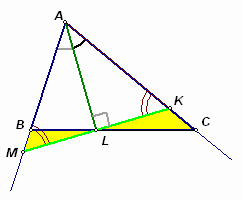
Первый способ. Через точку С проведем прямую, параллельную KM, N – точка ее пересечения с лучом АВ (см. рис. 2а). По теореме о пропорциональных отрезках ![]() . Пусть ВМ = 2x; MN = 3x, тогда, учитывая, что AN = AC, получим: АВ + 5x = АС. Следовательно, x = 0,4; ВМ = 0,8; АK = АМ = 4,8.
. Пусть ВМ = 2x; MN = 3x, тогда, учитывая, что AN = AC, получим: АВ + 5x = АС. Следовательно, x = 0,4; ВМ = 0,8; АK = АМ = 4,8.
Второй способ
. Пусть Ð BLM = Ð CLK = a , Ð AMK = Ð AKM = b (см. рис. 2б). Применим теорему синусов к треугольникам BLM и KLC. Соответственно получим:|
= |
= |
= |
= |
= |
= |
= |
|
|
¡ |
|||||||
|
¡ |
|||||||
|
¡ |
|||||||
|
¡ |
|||||||
|
¡ |
|||||||
|
¡ |
|||||||
|
¡ |
2.3.
Какое наибольшее количество ладей можно расставить на шахматной доске так, чтобы любая белая ладья не била никакую ладью по горизонтали, а любая черная ладья не била никакую ладью по вертикали?Ответ: 14 ладей.
Докажем, что больше, чем 14 ладей поставить нельзя. Заметим, что если в какой-то горизонтали стоит белая ладья, то никаких других ладей в этой горизонтали стоять не может. Следовательно, белых ладей не может быть более восьми. Если черных ладей на доске нет, то всего ладей – не более восьми, то есть заведомо меньше, чем 14. Если же на доске есть хотя бы одна черная ладья, то на одной горизонтали с ней белых ладей быть не может, значит, в этом случае, белых ладей не более, чем 7. Рассуждая аналогично про вертикали, получим, что и черных ладей не более, чем 7. Таким образом, ладей на доске – не более, чем 14.
Пример расстановки 14 ладей – см. рис. 3.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Известно, что m2 + n2 = 1, k2 + p2 = 1 и mk + np = 0. Найдите mn + kp.
Ответ: 0.
Первый способ. Из первых двух данных равенств следует наличие таких углов a и b , что m = cosa ; n = sina ; k = cosb ; p = sinb . Тогда третье равенство примет вид: cosa cosb + sina sinb = 0 Û cos(a – b ) = 0.
Следовательно, mn + kp = cosa
sina
+ cosb
sinb
= ![]() (sin2a
+ sin2b
) = sin(a
+ b
)cos(a
– b
) = 0.
(sin2a
+ sin2b
) = sin(a
+ b
)cos(a
– b
) = 0.
Второй способ. Рассмотрим векторы ![]() и
и ![]() . Из условия задачи следует, что
. Из условия задачи следует, что ![]() ,
, ![]() ,
, ![]() , то есть
, то есть ![]() . Отложим единичные векторы
. Отложим единичные векторы ![]() и
и ![]() от начала координат:
от начала координат: ![]() и
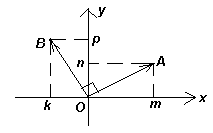
и ![]() , тогда точка В является образом точки А при повороте с центром О на 90°
(в одном из двух возможных направлений). Если этот поворот – против часовой стрелки (см. рис. 4), то из координатных формул поворота на 90°
(либо рассматривая равенство треугольников) получим, что
, тогда точка В является образом точки А при повороте с центром О на 90°
(в одном из двух возможных направлений). Если этот поворот – против часовой стрелки (см. рис. 4), то из координатных формул поворота на 90°
(либо рассматривая равенство треугольников) получим, что ![]() . Аналогично, в случае поворота по часовой стрелки, получим, что
. Аналогично, в случае поворота по часовой стрелки, получим, что ![]() . В обоих случаях mn + kp = 0.
. В обоих случаях mn + kp = 0.
Отметим, что две системы равенств, полученные при втором способе решения, соответствуют тому, что cos(a
– b
) = 0 Û
![]() или
или ![]() , где nÎ
Z, то есть
, где nÎ
Z, то есть ![]() или
или ![]() .
.
3.2. На сторонах ВС и CD квадрата ABCD произвольно выбраны точки Р и Q соответственно.
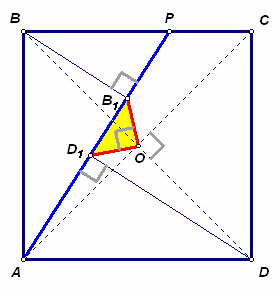
Из вершины В на отрезки АР и АQ опущены перпендикуляры BB1 и BB2, а из вершины D – перпендикуляры DD1 и DD2 соответственно. Докажите, что отрезки B1B2 и D1D2 равны и перпендикулярны.
Первый способ. Пусть диагонали квадрата пересекаются в точке О (см. рис. 5а). Рассмотрим поворот с центром О на 90° . Образом вершины В при этом повороте является вершина А, а образом прямой BB1 – прямая, ей перпендикулярная и проходящая через точку А. Следовательно, образ точки B1 лежит на прямой АР. Кроме того, образом вершины А при рассматриваемом повороте является вершина D, поэтому образ прямой АB1 – прямая, ей перпендикулярная и проходящая через точку D, то есть прямая DD1. Значит, образ точки B1 лежит и на прямой DD1. Таким образом доказано, что при повороте с центром О на 90° образом точки B1 является точка D1.
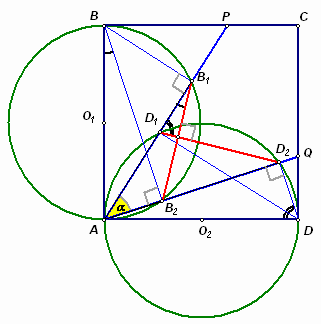
Аналогично доказывается, что при рассматриваемом повороте образом точки B2 является точка D2. Следовательно, образом отрезка B1B2 является отрезок D1D2, поэтому эти отрезки равны и перпендикулярны, что и требовалось (см. рис. 5б).
Второй способ. Пусть Ð
РАQ = a
. Заметим, что отрезок АВ виден из точек B1 и B2 под углом 90°
(см. рис. 5б). Следовательно, точки B1 и B2 лежат на окружности с диаметром АВ. По следствию из теоремы синусов: ![]() . Аналогично, из того, что точки D1 и D2 лежат на окружности с диаметром АD, получим, что
. Аналогично, из того, что точки D1 и D2 лежат на окружности с диаметром АD, получим, что ![]() . Так как АВ = AD, то B1B2 = D1D2.
. Так как АВ = AD, то B1B2 = D1D2.
Докажем теперь, что B1B2^ D1D2. Для этого достаточно доказать, что Ð AB1B2 + Ð B1D1D2 = 90° .
Это можно получить, например, так: Ð
AB1B2 + Ð B1D1D2 = Ð ABB2 + Ð ADD2 = (90° – Ð BAQ) + (90° – Ð DAQ) = 180° – (Ð BAQ + Ð DAQ) = 90° .3.3.
Полоска 1´ 100 разбита на единичные квадраты. В эти квадраты записывают числа 1, 2, ..., 100 следующим образом: сначала в какой-нибудь квадрат записывают число 1, затем в один из соседних квадратов записывают число 2, затем в один из соседних с уже занятыми квадратами записывают число 3, и так далее. Сколькими способами это можно проделать?Ответ: 299.
Первый способ. Заметим, что количество способов расстановки не изменится, если расставлять числа с конца. Число 100 могло оказаться только в одном из концов полоски – два возможных варианта. Уберем его, тогда останется полоска 1´ 99. Число 99 могло оказаться в одном из двух концов этой полоски – снова два возможных варианта. И так далее, каждый раз для того чтобы поставить очередное число у нас будет два варианта, пока мы не дойдем до единичного квадрата, в котором останется только одно свободное место. Значит всего 299 способов восстановить полоску с конца.
Эту же идею решения можно изложить по-другому. Будем расставлять числа от 1 до 100 по тем же правилам, что в условии задачи, но на бесконечной полоске. Запишем 1 в произвольный квадрат. Дальше будет два возможных варианта для того, чтобы поставить число 2, потом два возможных варианта для того, чтобы поставить число 3, и так далее. Получим, что количество вариантов выписать все числа от 1 до 100 по сформулированным правилам равно 299. В любом таком случае записанные числа займут какую-то полоску длины 100. Тогда в каждом случае их можно будет единственным способом сдвинуть так, чтобы они заняли исходную полоску 1´ 100.
Второй способ. Пусть 1 поставили на k-е место от начала. Если после этого выбрать, какие именно k – 1 чисел будут записаны перед 1, то вся запись определяется однозначно. Действительно, первые k – 1 мест будут заняты выбранными числами в порядке убывания, а 100 – k мест после 1 будут заняты оставшимися числами в порядке возрастания.
Выбрать k – 1 число из 99 чисел можно ![]() способами. Так как k может быть любым числом от 1 до 100, то общее количество способов равно:
способами. Так как k может быть любым числом от 1 до 100, то общее количество способов равно: ![]() .
.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Число а является корнем уравнения x3 – 3x2 + 5x – 17 = 0, а число b – корнем уравнения x3 – 3x2 + 5x + 11 = 0. Какие значения может принимать a + b?
Ответ: a + b = 2.
Так как x3 – 3x2 + 5x = (x3 – 3x2 + 3x – 1) + (2x + 1) = (x – 1)3 + (2x + 1), то исходные уравнения можно записать так: (x – 1)3 + 2(x – 1) – 14 = 0 и (x – 1)3 + 2(x – 1) + 14 = 0.
Далее можно рассуждать по-разному.
Первый способ. Поскольку числа а и b соответственно являются корнями полученных уравнений, то выполняются равенства: (a – 1)3 + 2(a – 1) = 14 и (b – 1)3 + 2(b – 1) = –14.
Пусть
a – 1 = m, b – 1 = n, тогда складывая эти равенства почленно, получим: m3 + 2m + n3 + 2n = 0 Û (m + n)(m2 – mn + n2) + 2(m + n) = 0 Û (m + n)(m2 – mn + n2 + 2) = 0.Так как
m2 – mn + n2 + 2 = (m – 0,5n)2 + 0,75n2 + 2 > 0, то m + n = 0. Следовательно, a + b – 2 = 0 Û a + b = 2.Второй способ. Пусть z = x – 1, тогда полученные уравнения примут вид: z3 + 2z = 14 и z3 + 2z = –14. Функция y = z3 + 2z возрастает (сумма возрастающих функций), поэтому каждое из этих уравнений имеет не более одного корня. Заметим, что если число с - корень первого уравнения, то число –с – корень второго. Следовательно, a – 1 = c, b – 1 = –c, то есть a + b = (c + 1) + (–c + 1) = 2.
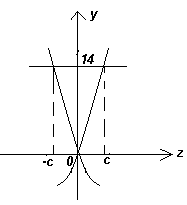
Эту же идею можно реализовать иначе. Уравнение z3 + 2z = –14 равносильно уравнению (–
z)3 – 2z = 14, а графики функций f(z) = z3 + 2z и g(z) = (–z)3 – 2z симметричны относительно оси ординат (эскиз – см. рис. 6). Следовательно, точки пересечения графиков с прямой y = 14 также симметричны относительно оси y, значит их абсциссы – противоположны. Поэтому a – 1 + b – 1 = 0 Û a + b = 2.Отметим, что важную роль в приведенных рассуждениях сыграла нечетность функции
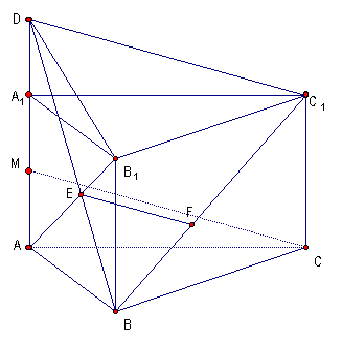
f(z) = z3 + 2z.4.2. Точка М – середина ребра АА1 треугольной призмы АBCA1B1C1. На прямой АВ1 выбрана точка Е, а на прямой ВС1 – точка F так, что прямые EF и СМ параллельны. Найдите ![]() .
.
Ответ: ![]() .
.
Первый способ. Так как EF
|| СМ, а прямая СМ лежит в плоскости AA1C, то EF || AA1C (см. рис. 7а). Плоскость BEF содержит прямую EF и пересекает плоскость AA1C по прямой DC1, значит, DC1 || EF. Таким образом, DC1 || CM.Следовательно, MCC1D – параллелограмм, значит, CM = C1D. Кроме того, так как М – середина АА1, то из равенства прямоугольных треугольников С1
A1D и САМ следует, что DA1 = MA = A1M. Из подобия треугольников ВЕВ1 и DEA следует, что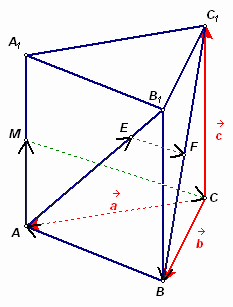
Второй способ. Рассмотрим тройку некомпланарных векторов: ![]() ,
, ![]() ,
, ![]() в качестве базисных (см. рис. 7б). Пусть также
в качестве базисных (см. рис. 7б). Пусть также ![]() ,
, ![]() . Тогда
. Тогда ![]() ,
, ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
Так как EF
|| СМ, то векторыСледовательно, ![]() =
= ![]() . В силу теоремы о единственности разложения любого вектора пространства по трем некомпланарным векторам, полученное уравнение равносильно системе:
. В силу теоремы о единственности разложения любого вектора пространства по трем некомпланарным векторам, полученное уравнение равносильно системе: 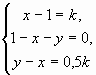 Исключив из нее переменные
Исключив из нее переменные
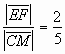 .
.
4.3. Можно ли в десятичной записи числа А = 28999 изменить ровно одну цифру так, чтобы оно стало простым?
Ответ: нет, нельзя.
Число 28999 – четное, значит его последняя цифра четная. Поэтому, если менять не последнюю цифру, то число останется четным, то есть не может стать простым (оно заведомо больше, чем 2). Значит, осталось разобрать возможные случаи изменения последней цифры.
Найдем последнюю цифру в десятичной записи числа 28999. Для удобства записи используем, что последняя цифра в десятичной записи числа является остатком от деления этого числа на 10. Тогда: 281 º 8 (
mod10); 282 º 82 º 4 (mod10); 283 º 83 º 2 (mod10); 284 º 84 º 6 (mod10); 285 º 85 º 8 (mod10), то есть остатки повторяются с периодом 4. Значит, 28999 º 283 º 2 (mod10).Заметим теперь, что число 28 дает остаток 1 при делении на 3, значит, число 28999 также дает остаток 1 при делении на 3. Переберем все варианты замены последней цифры числа 28999 и покажем, что в каждом случае полученное число является составным:
1) Замена последней цифры на другую четную цифру не меняет четности данного числа.
2) Замена последней цифры на 1 означает, что данное число уменьшится на 1, то есть станет равно 28999 – 1 = (28 – 1)(28998 + 28998 + ... + 1). Тогда оно делится на 27.
3) Замена последней цифры на 3 означает, что данное число увеличится на 1, то есть станет равным 28999 + 1 = (28 + 1)(28998 – 28998 + ... + 1). Тогда оно делится на 29.
4) Замена последней цифры на 5 означает, что полученное число кратно 5.
5) Замена последней цифры на 7 означает, что полученное число станет равно 28999 + 5 и будет делиться на 3, так как 28999 º 1 (
mod3).6)
Замена последней цифры на 9 означает, что полученное число будет равно 28999 + 7 и будет делится на 7.Отметим, что очень сложно доказывать простоту достаточно большого числа, поэтому в большинстве подобных задач можно заранее предугадать ответ, а именно, что рассматриваемое число окажется составным.
Пятый тур (1
5 минут; каждая задача – 7 баллов).5.1. Известно, что уравнение x4 + px2 + q = 0 имеет ровно три корня. Сколько корней имеет уравнение x4 + qx2 + p = 0?
Ответ: два корня.
Заметим, что если число
x0 – корень уравнения x4 + px2 + q = 0, то и число –x0 является корнем этого уравнения. Следовательно, если такое уравнение имеет ровно три корня, то один из них равен 0. Значит, q = 0, то есть первое уравнение имеет вид: x4 + px2 = 0 Û x2(x2 + p) = 0. Наличие трех корней у такого уравнения означает, что p < 0.Второе уравнение при
q = 0 имеет вид: x4 + p = 0. При p < 0 оно имеет два корня: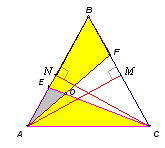
5.2. На боковых сторонах АВ и ВС равнобедренного треугольника АВС взяты точки Е и F соответственно. Отрезки ЕС и FА пересекаются в точке О. Докажите, что если площадь четырёхугольника ВЕОF равна площади треугольника АСО, то АЕ = ВF.
Из равенства площадей в условии задачи следует, что равновелики треугольники АВ
F и АСЕ, так как их площади получаются прибавлением площади треугольника ЕОА к равным площадям (см. рис. 8). Так как треугольник АВС – равнобедренный, то его высоты АM и СN равны, при этом АM и СN являются также высотами треугольников ABF и CAE соответственно. Следовательно, будут равны и соответствующие этим высотам основания, то есть ВF = АЕ, что и требовалось.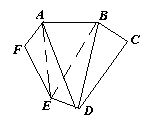
5.3. Существует ли выпуклый шестиугольник, у которого длина одной из сторон равна 1, а длины всех диагоналей – целые числа
?Ответ
: нет, не существует.Пусть шестиугольник АВСDEF со стороной АВ = 1 удовлетворяет условию задачи (см. рис. 9). Рассмотрим треугольник АВD: из неравенства треугольника следует, что |BD – АВ| < AD < BD + АВ, то есть BD – 1 < AD < BD + 1. Учитывая, что длины BD и AD – целые, получим, что AD = BD.
Аналогичное рассуждение можно провести и для треугольника АВЕ. Из того, что треугольники АВD и АВЕ – равнобедренные с основанием АВ следует, что точки D и Е лежат на серединном перпендикуляре к стороне АВ. Тогда вершины А и В лежат в разных полуплоскостях относительно прямой DE, что противоречит выпуклости шестиугольника.