11 класс
Первый тур (10 минут; каждая задача – 6 баллов).
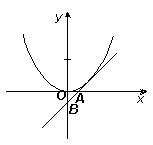
1.1.
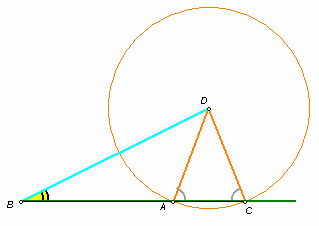
Касательная к графику y = x2 пересекает координатные оси в точках А и В так, что ОА = ОВ. Найдите площадь треугольника АОВ.Ответ: ![]() .
.
Из симметрии графика функции y = x2 следует, что указанным свойством обладают две касательные, симметричные относительно оси ординат. Так как треугольники, отсекаемые ими от осей координат, симметричны, то достаточно рассмотреть любую их них (см. рис. 1).
Треугольник ОАВ – прямоугольный и равнобедренный, значит, угол наклона касательной к оси x равен 45°
, следовательно, уравнение касательной имеет вид: y = x + a. Тогда абсцисса точки касания может быть найдена из соотношения y’(x0) = 1, то есть 2x0 = 1 Û
x0 = ![]() . Так как точка
. Так как точка ![]() принадлежит прямой y = x + a, то
принадлежит прямой y = x + a, то ![]() .
.
Таким образом, ОА = ОВ = ![]() , а площадь треугольника ОАВ равна
, а площадь треугольника ОАВ равна ![]() .
.
1.2.
Существует ли многогранник, у которого все грани – равнобокие трапеции?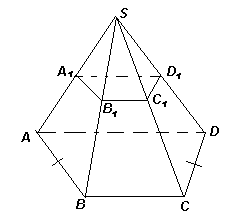
Ответ: да, существует.
Рассмотрим, например, пирамиду SABCD с равными боковыми ребрами, в основании которой лежит равнобокая трапеция ABCD (такая пирамида существует, поскольку равнобокая трапеция является вписанным четырехугольником; см. рис. 2). Проведем сечение пирамиды SABCD, параллельное основанию. Получим усеченную пирамиду ABCDA1B1C1D1, которая является искомой.
Действительно, сечение пирамиды, параллельное основанию, подобно основанию, а точки пересечения плоскости сечения с боковыми ребрами делят эти ребра в одном и том же отношении.
1.3. Найдите все натуральные решения уравнения n2 + 2n – n! = 0.
Ответ: n = 4.
Преобразуем исходное уравнение: n2 + 2n – n! = 0 Û n! = n(n + 2) Û (n – 1)! = n + 2. Непосредственной проверкой убеждаемся, что числа 1, 2 и 3 решениями полученного уравнения не являются, а число 4 – является.
Других решений нет, так как при n > 4 выполняется неравенство: (n – 1)! > 2(n – 1) > n + 2.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Найдите все положительные решения системы уравнений 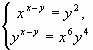 .
.
Ответ: (1; 1), (![]() – 1;
– 1; ![]() + 1).
+ 1).
Перемножим уравнения системы почленно: ![]() Û
Û
![]() Û
Û
1) 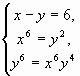
2) 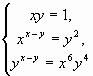
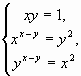 Û
Û
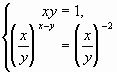 Û
Û
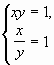 или
или 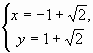 .
.
2.2. В параллелограмме АВСD диагональ АС вдвое больше стороны АВ. На стороне ВС выбрана точка K так, что Ð ADB = Ð KDB. В каком отношении точка K делит сторону ВС?
Ответ: ![]() .
.
Пусть О – точка пересечения диагоналей АС и
BD (см. рис. 3). Так как Ð KBD = Ð ADB = Ð KDB, то BK = DK, то есть KO – высота равнобедренного треугольника BKD.Кроме того, из условия задачи следует, что
AO = AB. Проведем высоту AN равнобедренного треугольника ВАО и продолжим ее до пересечения с прямой ВС в точке М. Так как N – середина ВО и MN || KO, то BM = MK (по теореме Фалеса). Аналогично, так как О – середина АС и OK || AM, то MK = KC. Следовательно,Во второй части решения можно было рассуждать иначе. Пусть М – середина В
K, тогда MO – средняя линия треугольника BDK, значит,2.3. Найдите все тройки (p; q; r) простых чисел, для которых числа |p – q|, |q – r| и |r – p| также являются простыми.
Ответ: (2; 5; 7) и еще пять троек, получаемых из этой с помощью перестановок.
Из условия задачи следует, что числа p, q и r попарно различны. Пусть p < q < r. Тогда p = 2, иначе среди трех указанных модулей разности найдутся два различных четных числа, значит, хотя бы одно из них не будет простым.
Рассмотрим число r – q. Так как числа r и q – нечетные, то r – q = 2. Таким образом, простыми должны являться числа: r, q = r – 2 и |p – q| = |q – 2| = r – 4. Но среди трех последовательных нечетных чисел всегда есть число, кратное 3. Так как все три числа – простые, то это числа 3, 5 и 7. Следовательно, p = 2, q = 5 и r = 7.
Очевидно, что любая перестановка найденных чисел также удовлетворяет условию задачи.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Вычислите ![]() , если
, если ![]()
![]() .
.
Ответ: 0.
Используем, что ![]() . Тогда данное равенство примет вид:
. Тогда данное равенство примет вид: ![]() Û
Û
![]() .
.
Так как ![]() и
и ![]() , то равенство достигается тогда и только тогда, когда
, то равенство достигается тогда и только тогда, когда ![]() или
или ![]() . Следовательно,
. Следовательно, ![]() или
или ![]() , то есть
, то есть ![]() = 0.
= 0.
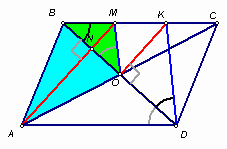
3.2. В треугольнике АВС: R1 и R2 – радиусы окружностей, проходящих через вершину С и касающихся прямой АВ в точках А и В соответственно. Найдите радиус окружности, описанной около треугольника АВС.
Ответ: ![]()
Пусть О1 и О2 – центры окружностей, заданных в условии задачи, О – центр окружности, описанной около треугольника АВС,
R – ее радиус.Первый способ. Проведем диаметры
AA1 и BB1 окружностей с центрами О1 и О2 соответственно, перпендикулярные прямой АВ (см. рис. 4а). Тогда треугольник А1СA – прямоугольный, значит, Ð СA1B = Ð СAB (каждый из них дополняет угол САА1 до прямого угла). Следовательно,Перемножим полученные равенства почленно, тогда ![]() .
.
По следствию из теоремы синусов для треугольника АВС: ![]() и
и ![]() . После перемножения этой пары равенств получим:
. После перемножения этой пары равенств получим: ![]() .
.
Таким образом, ![]() .
.
Равенство двух пар углов, отмеченных на чертеже, можно было получить, не проводя диаметры, а используя теорему об угле между касательной и хордой.
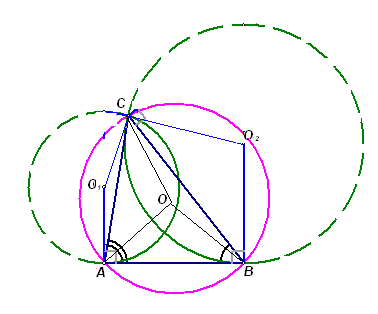
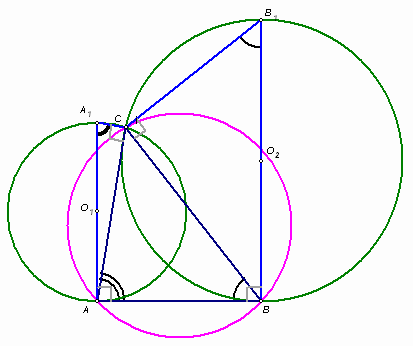
Второй способ. Проведем отрезки, соединяющие точку О со всеми вершинами треугольника АВС, точку О1 – с вершинами А и С, а точку О2 – с вершинами В и С (см. рис. 4б). Угол САВ является вписанным для окружности с центром О и углом между касательной и хордой для окружности с центром О1, значит, центральные углы этих окружностей, опирающиеся на соответствующие дуги, равны: Ð СО
B = Ð СО1A. Следовательно, равнобедренные треугольники СОB и СО1A подобны, поэтому,Аналогично, Ð СОA
= 2Ð СВA = Ð СО2B, то есть подобны треугольники. СО2B и СОA, значит,3.3. В турнире по хоккею участвовало несколько команд. Каждая команда должна была сыграть с каждой по одному матчу. Но в ходе турнира ровно половина команд была дисквалифицирована и эти команды выбыли из турнира. В результате в турнире было сыграно 77 матчей. Оказалось, что все дисквалифицированные команды сыграли одинаковое количество матчей, причем они успели провести между собой все положенные встречи. Сколько команд было в турнире первоначально?
Ответ: 14 команд.
Из условия задачи следует, что количество команд, стартовавших в турнире, было четным числом 2n. Тогда n команд было дисквалифицировано, причем они сыграли между собой ![]() матчей. Такое же количество матчей сыграли между собой и n оставшихся команд
матчей. Такое же количество матчей сыграли между собой и n оставшихся команд
Несложно проверить, что, как
n = 1, так и k = 1 решениями полученного уравнения не являются. Следовательно, второй множитель больше первого, значит,
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Каждое из чисел а, b, c и d лежит на отрезке [2; 4]. Докажите, что выполняется неравенство: 25(ab + cd)2 ³ 16(a2 + d2)(b2 + c2).
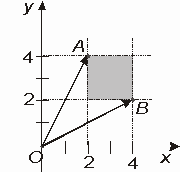
Заметим, что доказываемое неравенство равносильно неравенству ![]() .
.
Рассмотрим два вектора в декартовой системе координат: ![]() и
и ![]() . Тогда
. Тогда ![]() ;
; ![]() ;
; ![]() , то есть доказываемое неравенство имеет вид:
, то есть доказываемое неравенство имеет вид: ![]() .
.
Пусть числа а, b, c и d принадлежат [2; 4]. Тогда точки А и В принадлежат закрашенному квадрату (см. рис. 5). Наименьшее значение косинуса угла АОВ достигается при наибольшем возможном значении этого угла, то есть если точки А и В имеют координаты (2; 4) и (4; 2). Тогда ![]() . В остальных случаях
. В остальных случаях ![]() , что и требовалось.
, что и требовалось.
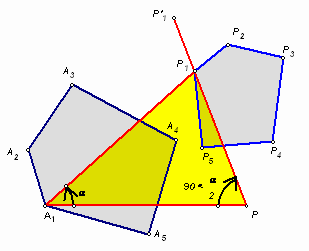
4.2. На плоскости заданы выпуклый n-угольник А1А2 ... An площади S и произвольная точка Р. Повернув точку Р на один и тот же заданный угол a относительно каждой из вершин данного многоугольника, получим новый n-угольник. Найдите его площадь.
Ответ: 2
S(1 – cosa ).Пусть
P1 – образ точки Р при указанном в условии задачи повороте (см. рис. 6). Тогда треугольник РА1Р1 – равнобедренный (с основанием РР1), то есть Ð А1РР1 = Ð А1Р1Р = 90° –Так как поворотная гомотетия с коэффициентом k является преобразованием подобия с коэффициентом |k| (композиция движения и подобия), то ![]() , где S’ – площадь P1P2...Pn. Из треугольника РА1Р1 вычислим коэффициент подобия:
, где S’ – площадь P1P2...Pn. Из треугольника РА1Р1 вычислим коэффициент подобия: ![]() .
.
Следовательно, ![]() .
.
Отметим, что условие выпуклости исходного многоугольника является избыточным.
4.3. Римский патриций решил устроить большой праздник и для этого приготовил 240 бочек вина. Однако к нему в подвал пробрался враг, который подсыпал яд в одну из бочек. У патриция есть 5 драгоценных камней со следующим свойством: если камень окунуть в отравленное вино, то он почернеет в течение часа (в какой момент – неизвестно). До праздника осталось ровно два часа. Патриций готов пожертвовать камнями, чтобы найти отравленную бочку. Объясните, каким образом это можно сделать.
Первый способ. Приготовим 5 больших бокалов, в каждый из которых будем окунать один из 5 камней, и будем смешивать в них содержимое бочек по следующей схеме: вино из первой бочки нальем во все бокалы, затем для каждой четверки камней (всего таких четверок 5) нальем вина еще из двух бочек (итого будет использовано еще 5´ 2 = 10 бочек), для каждой тройки камней (таких троек 10) нальем вина из четырех новых бочек (то есть использовано еще 10´ 4 = 40 бочек), для каждой пары камней (их также 10) – еще из восьми бочек (еще 10´ 8 = 80 бочек), и для каждого камня в отдельности добавим вина еще из 16 бочек (то есть использовано еще 80 бочек).
Таким образом, в первый час будет использовано 1 + 10 + 40 + 80 + 80 = 211 бочек.
Если почернеют все камни, то отравлено вино из первой бочки. Если почернеет какая-то четверка камней, то отравлено вино в какой-то из двух бочек. В одну из них в начале второго часа мы окунем еще не почерневший камень, что позволит определить отравленную бочку. Если почернеет какая-то тройка камней, то на подозрении будут четыре бочки. В начале второго часа окунем в первую бочку оба не почерневших камня, во вторую бочку – один, в третью – другой, что позволит также определить отравленную бочку. Аналогичную схему в начале второго часа применим и в случаях, когда останутся три или четыре не почерневших камня. Если же ни один камень не почернеет, то с их помощью нужно будет выбрать одну из 29 неиспользованных бочек, что можно сделать по аналогичной схеме, так как 29 < 32 = 25.
Понятно, что задача легко обобщается для случая, когда камней n, а бочек – не более, чем 3n, так как по сути мы используем, что ![]() .
.
Второй способ. Занумеруем камни числами от 1 до 5, а бочки – в троичной системе счисления, начиная с нуля. Так как 240 < 243 = 35, то номера всех бочек будут не более чем пятизначными числами. Если в номере меньше пяти цифр, то для удобства спереди добавим нули так, чтобы все числа стали пятизначными. Еще 3 бочки можно залить водой.
|
Камень 1 |
Камень 2 |
|||
|
I час |
II час |
I час |
II час |
|
|
00 |
+ |
+ |
||
|
0 1 |
+ |
+ |
||
|
02 |
+ |
|||
|
10 |
+ |
+ |
||
|
11 |
+ |
+ |
||
|
12 |
+ |
|||
|
20 |
+ |
|||
|
21 |
+ |
|||
|
22 |
||||
В начале первого часа окунём камень с номером
k в каждую бочку, у которой в k-ом разряде номера стоит цифра 0. Рассмотрим камни, не почерневшие по истечении первого часа. В номере ядовитой бочки в разрядах, соответствующих номерам этих камней, могут стоять только цифры 1 или 2, а в разрядах, соответствующих номерам почерневших камней, стоят нули. Зафиксируем числа с соответствующими нулевыми разрядами, и в начале второго часа окунем все не почерневшие камни во все бочки, в номерах которых в разрядах, соответствующих номерам камней, стоит цифра 1. Если камень почернел, то в номере ядовитой бочки соответствующий разряд равен 1, а если нет, то 2. Тем самым номер отравленной бочки однозначно определяется.Для того, чтобы наглядно представить описанное соответствие, приведем алгоритм действий в виде таблицы для двух камней и 9 = 32 бочек (знак «+» показывает, какой камень и в какой час нужно окунуть в бочку с данным номером).
Пятый тур (15 минут; каждая задача – 7 баллов).
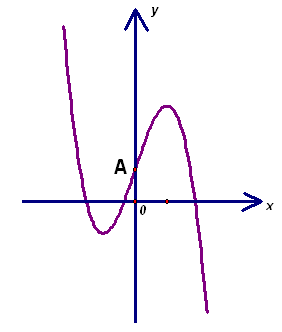
5.1. Точка А – центр симметрии графика функции f(x)
= ах3 + bх2 + сх + d (см. рисунок). Сравните коэффициенты а, b, с и d с нулем.Ответ:
a < 0; b = 0; c > 0; d > 0.1)
d = f(0) > 0.2
) Так какПо-другому: f(x)
= a(x – x1)(x – x2)(x– x3), где x1 < x2 < x3. Так как при x > x3 f(x) < 0, то а < 0.3) Функция
g(x)= ах3 + bх2 + сх является нечетной, следовательно, b = 0 (при любых значениях x выполняется равенство g(–x) = –g(x) Þ –ах3 + bх2 – сх = –ах3 – bх2 – сх Û bх2 = 0).4) На отрезке, содержащем x = 0, ![]() возрастает, следовательно, c = f’(0) > 0.
возрастает, следовательно, c = f’(0) > 0.
По-другому: f’(x) = 3ax2 + 2bx + c. Так как функция имеет две точки экстремума, то уравнение f’(x) = 0 имеет два корня, то есть b2 – 3ac > 0. При a < 0 ![]() .
.
Найдя знаки некоторых коэффициентов, для поиска знаков остальных коэффициентов можно также использовать теорему Виета.
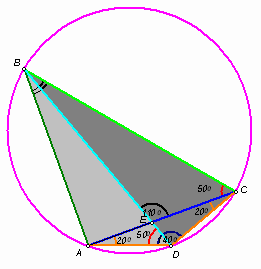
5.2.
В четырехугольнике АВСD диагональ BD является биссектрисой угла АВС, Е – точка пересечения диагоналей, AD = DC, Ð ADC = 140° , Ð BEC = 110° . Найдите угол АСВ.Ответ: 50° .
Первый способ. Рассмотрим треугольники BAD и BCD: BD – общая сторона, AD = CD и Ð ABD = Ð СBD (см. рис. 6а). В такой ситуации возможны два случая (*):
1) Ð ВAD = Ð ВСD, и тогда эти треугольники равны.
2) Ð ВAD + Ð ВСD = 180° , и тогда эти треугольники различны.
Первый случай невозможен, так как по условию Ð BEC = 110° , то есть смежный с ним угол – острый.
Во втором случае четырехугольник АВСD является вписанным, тогда Ð
ADC = 40°
, значит Ð
АСВ = 180°
– Ð
BEC – ![]() Ð
ADC = 50°
.
Ð
ADC = 50°
.
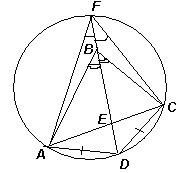
*Это следует, например, из решения задачи на построение треугольника по двум сторонам и углу, противолежащему одной из этих сторон (см. рис. 6б) или из теоремы синусов (см. рис. 6а): ![]() =
= ![]() , то есть
, то есть ![]() .
.
Второй способ. Так как ВЕ – биссектриса треугольника АВС, то ![]() . Рассмотрим окружность, описанную около равнобедренного треугольника ADC. Предположим, что эта окружность пересекает прямую BD в точке F, отличной от В (см. рис. 6в). Тогда FE – биссектриса треугольника AFC, значит,
. Рассмотрим окружность, описанную около равнобедренного треугольника ADC. Предположим, что эта окружность пересекает прямую BD в точке F, отличной от В (см. рис. 6в). Тогда FE – биссектриса треугольника AFC, значит, ![]() . Таким образом, точки В и F принадлежат ГМТ, отношение расстояний которых от точек А и С равно
. Таким образом, точки В и F принадлежат ГМТ, отношение расстояний которых от точек А и С равно ![]() . Этим ГМТ является либо прямая (если k = 1), либо окружность, называемая окружностью Аполлония (если k ¹
1).
. Этим ГМТ является либо прямая (если k = 1), либо окружность, называемая окружностью Аполлония (если k ¹
1).
Первый случай невозможен, так как если АЕ = ЕС, то угол ВЕС – прямой. Второй случай невозможен, так как прямая BD не может иметь с окружностью Аполлония три общие точки: Е, В и F. Следовательно, рассмотренная изначально окружность проходит через точку В. Вычисление искомого угла приведено выше.
5.3. Существует ли 2009-значное натуральное число N, для которого число M = NN + (N + 1)N + 1 является составным?
Ответ: да, существует.
Заметим, что существует четное 2009-значное число N, которое при делении на 3 дает в остатке 1, то есть N = 6k + 4 (среди 2009-значных таких чисел много). Тогда N + 1 = 6k + 5.
Так как N º 1 (mod 3), то и NN º 1 (mod 3) (это следует, например, из разложения числа (3m + 1)N по биному Ньютона).
Аналогично, N + 1 º –1 (mod 3) и число N + 1 – нечетное, значит, (N + 1)N + 1 º –1 (mod 3). Таким образом, M º 0 (mod 3), то есть является составным.