7 класс

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Существуют ли такие натуральные числа а и b, что число b является натуральной степенью числа a и число b в 16 раз больше числа а?

Ответ: да, существуют.

Возможные примеры: a = 2, b = 32 или a = 4, b = 64 или a = 16, b = 256.

Можно доказать, что других пар значений а и b, удовлетворяющих условию задачи, не существует. Действительно, из условия следует, что b = an и b = 16a, значит, an = 16a. Разделив обе части этого равенства на а (а – натуральное число), получим: an – 1 = 16. Так как n – также натуральное число, то а может принимать только три значения: 2, 4 или 16.

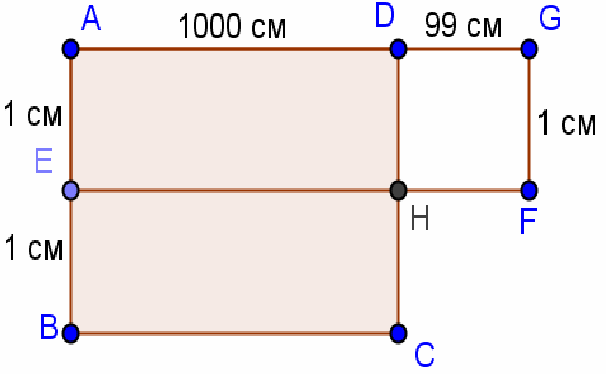
1.2. Одно из измерений прямоугольника увеличили на 99 см, а другое – уменьшили на 1 см, и получили новый прямоугольник. Можно ли утверждать, что площадь прямоугольника увеличилась? Ответ обоснуйте.

Ответ: нет, это утверждать нельзя.

Рассмотрим, например, прямоугольник ABCD, в котором АВ = 2 см, AD = 1000 см (см. рис. 1). После уменьшения стороны АВ на 1 см площадь прямоугольника уменьшилась на 1000 см2. Увеличив теперь сторону AD на 99 см, мы добавим к площади прямоугольника только 99 см2. Следовательно, площадь исходного прямоугольника уменьшилась.

Отметим, что возможен и более общий подход, а именно, если измерения исходного прямоугольника а см и b см, то измерения нового прямоугольника – (a + 99) см и (b – 1) см. Тогда разность площадей нового и исходного прямоугольников равна (a + 99)(b – 1) – ab = 99b – a – 99. Таким образом, площадь исходного прямоугольника увеличится, если выполняется неравенство 99b – a – 99 > 0, то есть а < 99(b – 1). Любые положительные значения а и b, не удовлетворяющие полученному неравенству, также могут служить в качестве контрпримера.

1.3. Незнайка лжет по понедельникам, вторникам и пятницам, а в остальные дни недели говорит правду. В какие дни недели Незнайка может сказать: «Я лгал позавчера и буду лгать послезавтра»? Ответ обоснуйте.

Ответ: по понедельникам, вторникам, средам, пятницам и воскресеньям.

Незнайка может сказать фразу, приведенную в условии, в двух случаях:

1) в те дни, когда он говорит правду, если за два дня до этого и через два дня после этого он лжет; 2) в те дни, когда он лжет, если за два дня до этого или через два дня после этого он говорит правду.

Последовательной проверкой всех семи дней недели можно убедиться, что этим условиям удовлетворяют все дни недели, кроме четверга и субботы.

 

Второй тур (15 минут; каждая задача – 7 баллов).

2.1. В доме двое механических часов: одни отстают на 15 минут в сутки, а другие на 10 минут в сутки спешат. Сегодня в полдень и те, и другие часы показывали правильное время. Когда в следующий раз они одновременно покажут правильное время?

Ответ: через 144 суток.

Первые часы отстают на 15 минут в сутки. Следовательно, через четверо суток они будут отставать на час, а через 48 суток отстанут на 12 часов, то есть впервые покажут правильное время. Вторые часы будут спешить на час через 6 суток, а правильное время впервые покажут, когда будут спешить на 12 часов, то есть по прошествии 72 суток.

Так как НОК(48; 72) = 144, то и те, и другие часы впервые покажут правильное время через 144 суток.

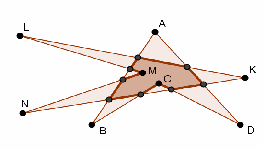
2.2. Можно ли так изобразить два четырехугольника, чтобы их общая часть (пересечение) оказалась десятиугольником?

Ответ: да, можно.

Например, см. рис. 2. Общая часть четырехугольников ABCD и KLMN является десятиугольником.

Отметим, что искомые четырехугольники должны быть невыпуклыми.

Также отметим, что больше чем десять вершин в пересечении двух четырехугольников получить нельзя. Действительно, каждая сторона любого из исходных четырехугольников может «порождать» либо одну сторону многоугольника – пересечения, либо две (если она пересекает две стороны другого четырехугольника, образующие плоский угол, который больше развернутого). Поскольку таких углов не больше двух, то количество сторон в пересечении не больше, чем 2× 2 + 6× 1 = 10.

2.3. В поезде Москва – Тьмутаракань ввели сплошную нумерацию мест в вагонах. Во всех вагонах одинаковое количество мест. Известно, что места 385 и 416 находятся в одном вагоне, а места 544 и 577 находятся в разных вагонах, причем эти вагоны – не соседние. Сколько мест в одном вагоне? Ответ обоснуйте.

Ответ: 32 места.

Поскольку места 385 и 416 находятся в одном вагоне, то количество мест в вагоне не меньше, чем 416 – 385 + 1 = 32. С другой стороны, между местами 544 и 577 находится 577 – 544 – 1 = 32 места. Это означает, что в одном вагоне не больше, чем 32 места. Таким образом, в вагоне ровно 32 места.

 

Третий тур (15 минут; каждая задача – 7 баллов).

3.1. При каких значениях k прямые у = kх и у = х + 1 пересекаются в первой координатной четверти?

Ответ: при k > 1.

Пусть M – точка пересечения данных прямых, тогда справедливы равенства и . Точка М располагается в первой координатной четверти тогда и только тогда, когда одновременно выполняются два неравенства: > 0 и > 0.

Выразим сначала , приравняв правые части записанных равенств: ; . При k = 1 это уравнение решений не имеет, поэтому , где k ¹ 1. Следовательно, > 0, если k > 1.

Выразим теперь , используя, например, что . Получим, что . При k > 1 неравенство > 0 заведомо выполняется. Таким образом, точка М находится в первой координатной четверти при k > 1.

Отметим, что при k = 1 данные прямые параллельны, а при k < 1 – пересекаются, но не в первой четверти. Совпадать эти прямые не могут ни при каких значениях k.

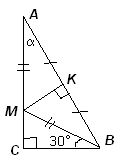
3.2. В прямоугольном треугольнике АВС точка K – середина гипотенузы АВ, а точка М делит катет АС в отношении 2 : 1 (считая от вершины А). Найдите острые углы треугольника АВС, если отрезок MK перпендикулярен АВ.

Ответ: 30° и 60° .

Проведем отрезок МВ, тогда МК – медиана и высота треугольника АМВ (см. рис. 3). Следовательно, треугольник АМB – равнобедренный: МB = МА. Тогда в прямоугольном треугольнике СВМ катет СМ в два раза меньше гипотенузы МВ, следовательно, угол СВМ равен 30°.

Пусть Ð САВ = a , тогда Ð АВМ = Ð САВ = a (по свойству равнобедренного треугольника). В прямоугольном треугольнике АВС сумма острых углов равна 90°, поэтому, 2a + 30° = 90°, то есть a = 30°. Следовательно, Ð САВ = 30°, Ð СВА = 60°.

В заключительной части решения можно было действовать иначе: в треугольнике СМВ один из острых углов равен 30° , поэтому другой острый угол равен 60° . Этот угол СМВ – внешний угол при вершине равнобедренного треугольника АМВ, поэтому он равен 2a , значит, a = 30°.

3.3. В шахматном турнире каждый участник сыграл с каждым по одной партии. Победитель выиграл у всех и набрал в 5 раз меньше очков, чем все остальные вместе. Сколько было участников? (Победа – 1 очко, ничья – 0,5 очка, поражение – 0 очков)

Ответ: 12 участников.

Пусть в турнире участвовало n человек, тогда каждый из них сыграл n – 1 партию. Всего в турнире было сыграно партий, при этом без участия победителя было сыграно – (n – 1) = партий.

Заметим, что в каждой партии между участниками распределяется 1 очко. Поэтому победитель набрал n – 1 очко, а все остальные вместе набрали очков. Учитывая условие задачи, составляем уравнение: = 5(n – 1). Так как n > 1, то решением уравнения является только n = 12.

Четвертый тур (20 минут; каждая задача – 8 баллов).

4.1. Существуют ли такие три различных числа а, b и с, что а(b – c) = b(c – a) = c(a – b)?

Ответ: нет, не существуют.

Первый способ. Пусть а(b – c) = b(c – a) = c(a – b) = x, тогда 3x = а(b – c) + b(c – a) + c(a – b) = ab – ac + bc – ba +ca – cb = 0, то есть x = 0.

Если а(b – c) = 0 и b ¹ c (по условию), то а = 0. Аналогично, если b(c – a) = 0 и c ¹ a, то b = 0. Таким образом, а = b, что противоречит условию.

Второй способ. Преобразуем равенство а(b – c) = b(c – a): ab – ac = bc – ab, то есть . Аналогично, из равенства b(c – a) = c(a – b) получим, что , а из равенства а(b – c) = c(a – b) получим, что .

Следовательно, каждое из трех чисел ab, bc и ac является средним арифметическим двух других. Если эти числа различны, то такое невозможно, поскольку среднее арифметическое любых двух различных чисел больше одного из них и меньше другого. Таким образом, ab = bc = ac. Но из равенства ab = bc и условия a ¹ c следует, что b = 0. Аналогично, из равенства bc = ac и условия a ¹ b следует, что c = 0. Значит, b = c, что противоречит условию задачи.

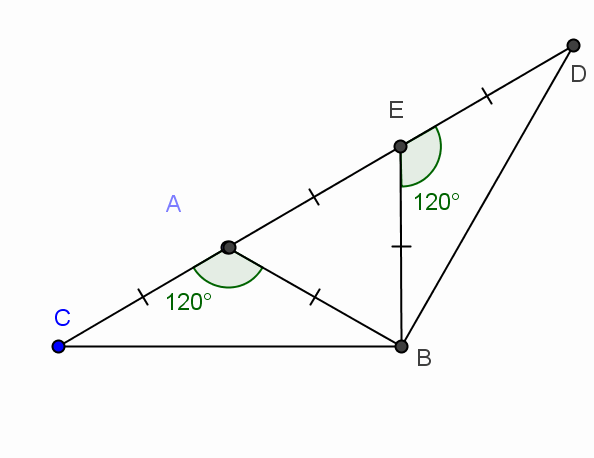
4.2. Треугольник ABC – равнобедренный, Ð BAC = 120° . На продолжении стороны AС за вершину A взята точка D так, что AD = 2AB. Докажите, что треугольник BDC – также равнобедренный.

Пусть Е – середина отрезка AD, тогда АЕ = АD = AB (см. рис. 4). Так как Ð BAC = 120° , то смежный с ним угол ВАЕ равен 60° . Таким образом, треугольник ВАЕ – равнобедренный с углом 60° при вершине, значит, треугольник ВАЕ – равносторонний.

Кроме того, . Значит, треугольники BAC и BED равны по двум сторонам и углу между ними. Следовательно, BD = BC, то есть треугольник BDC – равнобедренный.

Последнюю часть рассуждений можно провести иначе: так как медиана BЕ треугольника АВD равна половине стороны AD, к которой она проведена, то треугольник ABD – прямоугольный, Ð ABD = 90° . Поскольку Ð АСВ = Ð АВС = 30° , то Ð DВС = 120° . Тогда из треугольника CBD получим, что Ð CDB = 180° – (Ð CBD + Ð BCD) = 30° = Ð BCD. Таким образом, в этом треугольнике равны два угла, следовательно, треугольник BDC – равнобедренный.

4.3. На экране компьютера было записано число 123456789. Вася так вставил пробелы между некоторыми цифрами этого числа, что оно разбилось на несколько кусков, причем числа, записанные на любых двух кусках, оказались взаимно простыми. Какое наибольшее количество кусков могло при этом получиться? (Напомним, что взаимно простыми называются натуральные числа, у которых есть ровно один общий делитель – единица.)

Ответ: шесть.

Заметим, что из четырех четных цифр: 2, 4, 6 и 8 целый кусок может составить не более, чем одна. Остальные три обязаны войти в куски, состоящие из двух или более цифр (причём войти не в качестве последней цифры). Это значит, что кусков не может быть больше шести (три куска по две цифры и три куска по одной цифре).

Приведем один из возможных примеров разбиения данного числа на шесть кусков:

1 23 4 5 67 89.