8 класс

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Вычислите (не используя микрокалькулятор): .

Ответ: 2010.

= = = = 2010.

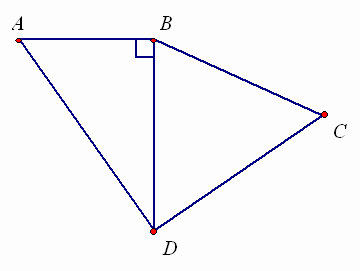
1.2. Определите вид четырехугольника, в котором каждая диагональ разбивает его на два прямоугольных треугольника. Ответ объясните.

Ответ: прямоугольник.

Пусть АВСD – искомый четырехугольник (см. рис. 1). Рассмотрим одну из его диагоналей, например, BD. По условию, треугольник АВD – прямоугольный. Докажем, что прямым может быть только угол с вершиной А.

Действительно, если, например, угол ABD – прямой, то угол ABC – тупой, что противоречит условию, так как треугольник ABC – уже не прямоугольный.

Аналогично, в любом из треугольников, получающихся при разбиении, прямой угол лежит напротив диагонали четырехугольника. Следовательно, вершинами прямых углов являются вершины четырехугольника, то есть АВСD – прямоугольник.

1.3. С полудня до полуночи Кот Ученый спит под дубом, а с полуночи до полудня рассказывает сказки. На дубе он повесил плакат: «Через час я буду делать то же самое, что делал два часа назад». Сколько часов в сутки эта надпись верна?

Ответ: 18 часов.

Выясним промежутки времени, в которые надпись неверна. Они начинаются за час до того момента, когда Кот меняет вид деятельности, и продолжаются еще 2 часа после этого момента. Таким образом, надпись неверна с 11 до 14 часов и с 23 часов до 2 часов, то есть 6 часов в сутки. В остальное время надпись верна, значит, она верна 18 часов в сутки.

 

Второй тур (15 минут; каждая задача – 7 баллов).

2.1. Найдите предпоследнюю цифру в десятичной записи числа S = 20092008 + 20092009.

Ответ: 1.

1) Так как 20092008 + 20092009 = 20092008(1 + 2009) = 20092008× 2010 = 20092008× 2000 + 20092008× 10, то предпоследняя цифра числа S совпадает с последней цифрой числа 20092008.

2) Последняя цифра числа 20092008 совпадает с последней цифрой числа 92008. Так как 92008 = 811004, то последняя цифра этого числа – 1.

Следовательно, предпоследняя цифра числа S – 1.

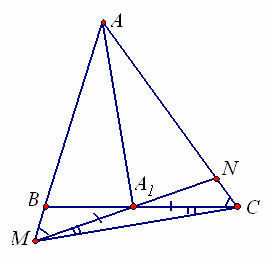
2.2. В треугольнике АВС длины сторон попарно различны. На сторонах АВ и АС угла ВАС выбираются точки М и N соответственно так, что АМ = АС и АN = АВ. Отрезок МN пересекается со стороной ВС в точке А1. Аналогично, на сторонах угла АВС выбираются точки K и L так, что BK = BC и BL = BA, В1 – точка пересечения KL и АС. Точка С1 на стороне АВ также определяется аналогично. Докажите, что прямые АА1, ВВ1 и СС1 пересекаются в одной точке.

Из условия задачи следует, что (АМ = АС, АN = АВ, угол A – общий, см. рис. 2), следовательно, . Кроме того, из равнобедренного треугольника AMС получим, что . Следовательно, , значит, треугольник A1CM – также равнобедренный: MA1 = CA1 Тогда (по трем сторонам), откуда следует, что , то есть AA1 – биссектриса угла CAB. Аналогично доказывается, что BB1 и СС1 – также биссектрисы треугольника АВС. Следовательно, эти три отрезка пересекаются в одной точке (центре окружности, вписанной в треугольник АВС).

Отметим, что по сути приведенное рассуждение показывает, что прямая АА1 является осью симметрии угла ВАС.

2.3. Имеются три слитка с массами 1, 2 и 3 кг. Процентные содержания золота в разных слитках – различны (но неизвестны). Каждый слиток надо разделить на три части и изготовить из них три новых слитка с теми же массами 1, 2 и 3 кг так, чтобы процентное содержание золота во всех новых слитках стало бы одинаковым (независимо от того, каким оно было в исходных кусках). Объясните, как это можно сделать.

Ответ: каждый слиток можно разделить в отношении 1 : 2 : 3 и сплавить вместе меньшие части кусков, средние и большие.

Суммарная масса кусков – 6 кг. Так как масса первого сплава составляет часть от этой суммы, масса второго сплава – часть, а масса третьего сплава – , то новые слитки будут иметь требуемые массы.

Объяснить, почему содержание золота в новых слитках станет одинаковым, можно по-разному.

Первый способ («арифметический»). Массы второго и третьего сплавов больше, чем масса первого сплава, в 2 и в 3 раза соответственно. При этом во второй сплав из каждого первоначального слитка взято в 2 раза больше золота, чем в первый сплав, а в третий сплав из каждого слитка взято в 3 раза больше золота, чем в первый.

Второй способ («алгебраический»). Пусть доля золота в первом слитке равна х, во втором – у, а в третьем – z. Тогда в сплаве, состоящем из меньших кусков, содержание золота равно: 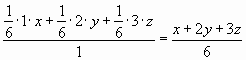. В сплаве, состоящем из средних кусков, содержание золота равно: 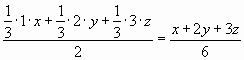. В сплаве, состоящем из больших кусков, содержание золота равно: .

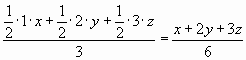Можно доказать, что способ, приведенный в ответе, – единственный (от школьников это не требуется).

 

Третий тур (20 минут; каждая задача – 8 баллов).

3.1. Разложите число 2202 + 1 на два множителя, каждый из которых не меньше миллиона.

Ответ: 2202 + 1 = (2101 + 251 + 1)(2101 – 251 + 1).

Пусть 250 = x, тогда исходное выражение примет вид 4x4 + 1. Разложим на множители это выражение: 4x4 + 1 = 4x4 + 4x2 + 1 – 4x2 = (2x2 + 1)2 – (2x)2 = (2x2 + 2x + 1)(2x2 – 2x + 1).

Таким образом, 2202 + 1 = (2101 + 251 + 1)(2101 – 251 + 1), что и требовалось, поскольку 2101 + 251 + 1 > 2101 – 251 + 1 > 2100 = (210)10 = 102410 > 10002 = 1000000.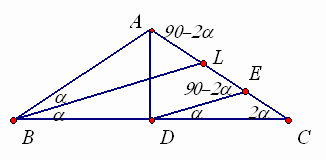

3.2. В равнобедренном треугольнике АВС с основанием ВС биссектриса BL вдвое больше высоты AD. Найдите углы треугольника.

Ответ: два угла по 36° и угол 108° .

Первый способ. Пусть Ð АВС = 2a . Проведем отрезок DE параллельно BL (точка E – на стороне AC, см. рис. 3а). Тогда угол AED – внешний для треугольника EDC, значит, Ð АED = a + 2a = 3a .

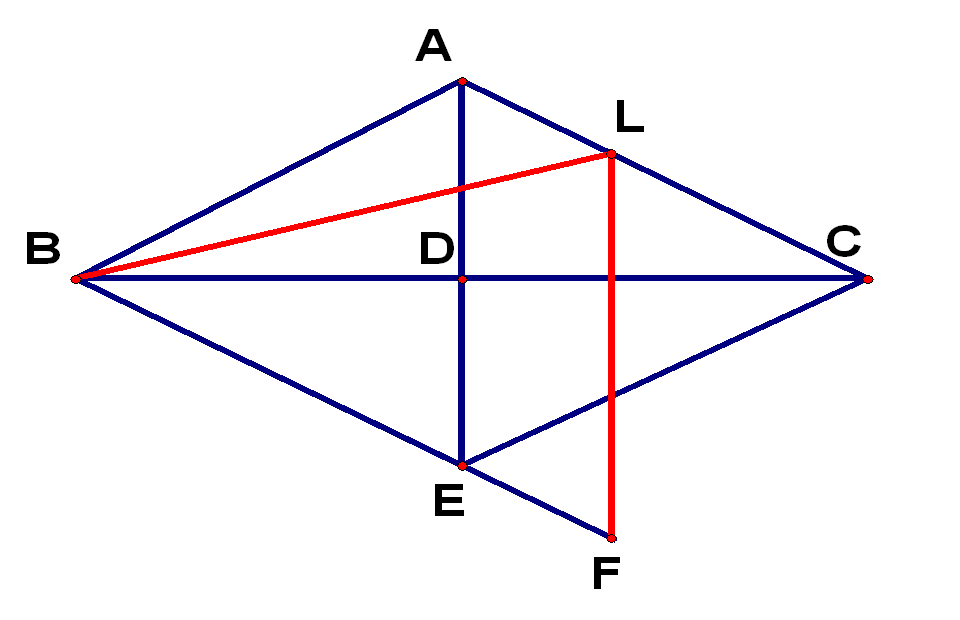
По теореме Фалеса точка Е – середина отрезка CL, то есть DE – средняя линия треугольника LBC. Следовательно, DE = BL = AD, то есть треугольник ADE – равнобедренный. Тогда Ð АED = Ð EAD = 90° – 2a .

Таким образом, 90° – 2a . = 3a Û a = 18° . Следовательно, Ð АBC = Ð ACB = 2a = 36° ; Ð BAC = 108° .

Второй способ. Отметим на луче AD такую точку Е, что ED = AD, тогда АЕ = ВL (см. рис. 3б). Так как высота AD является также и медианой треугольника АВС, то получившийся четырехугольник АВЕС – ромб. Через точку L проведем прямую LF, параллельную АЕ (F – точка ее пересечения с прямой BF). По построению, АLFЕ – параллелограмм, следовательно, LF = АЕ = ВL, то есть треугольник ВLF – равнобедренный.

Пусть Ð LВС = a , тогда Ð АСB = Ð АВС = 2a , Ð DАС = Ð LFВ = Ð LВF = 3a . Из прямоугольного треугольника DАС получим, что 2a + 3a = 90° , то есть a = 18° .

Следовательно, Ð АBC = Ð ACB = 36° ; Ð BAC = 108° .

3.3. После окончания учебного года Миша решил вырвать из своего учебника математики все листы, на каждом из которых сумма номеров страниц (на обеих сторонах листа) является квадратом целого числа, а Гриша собрался удалить все листы, для которых эта же сумма является кубом целого числа. Кто из них нанесет учебнику больший ущерб?

Ответ: если в учебнике не меньше, чем 7 листов, то больший ущерб нанесет Гриша, иначе – ущерба не будет.

На каждом листе одна страница имеет нечетный номер, а другая – четный, причем нечетное число меньше четного. Запишем нечетное число в виде 2n – 1, тогда четное будет равно 2n, где n – натуральное число. Сумма номеров страниц на одном листе равна 4n – 1.

Докажем, что число такого вида (имеющее остаток 3 при делении на 4) не может быть квадратом целого числа. Действительно, если число k – четное, то есть k = 2m (m – целое), то k2 = 4m2, значит, его квадрат делится на 4 без остатка. Если же число k нечетно, то есть k = 2m – 1, то k2 = (2m – 1)2 = 4m2 – 4m + 1 = 4(m2 – m) + 1, значит, его квадрат имеет остаток 1 при делении на 4.

Таким образом, Миша в любом случае не вырвет из учебника ни одного листа. При этом, 13 + 14 = 27 = 33, то есть если в учебнике – хотя бы 7 листов, то Гриша наверняка сможет вырвать седьмой лист с номерами страниц 13 и 14.

Отметим, что кубы нечетных чисел имеют тот же остаток при делении на 4, что и сами числа, так как (4m ± 1)3 = 64m3 ± 48m2 + 12m ± 1 = 4(16m3 ± 12m2 + m) ± 1. Поэтому следующий лист учебника, который сможет вырвать Гриша, – восемьдесят шестой, поскольку 73 = 343 = 171 + 172.

 

 

Четвертый тур (25 минут; каждая задача – 9 баллов).

4.1. Сравните x и z, если известно, что x + yzt = y + ztx = z + txy = t + xyz и x > y, z > t.

Ответ: x = z.

Первый способ. 1) Преобразуем первое равенство: x + yzt = y + ztx Û x – y = zt(x – y). Так как x ¹ y, то zt = 1.

2) Аналогично, из последнего равенства: z + txy = t + xyz Û z – t = xy(z – t). Так как z ¹ t, то xy = 1.

3) Поскольку x > y и xy = 1, то 0 < y < 1 или y < –1. Аналогично, z > t и zt = 1, значит, 0 < t < 1 или t < –1. Следовательно, yt ¹ 1.

4) Преобразуем еще одно данное равенство: x + yzt = z + txy Û (x – z) – yt(x – z) = 0 Û (x – z)(1 – yt) = 0. Так как yt ¹ 1, то x = z.

Второй способ (для тех, кто уже знаком с квадратными уравнениями). Заметим, что zt ¹ 0, иначе из первого равенства следует, что x = y. Аналогично, xy ¹ 0, иначе из последнего равенства следует, что z = t. Таким образом, x ¹ 0, y ¹ 0, z ¹ 0 и t ¹ 0.

Пусть x + yzt = y + ztx = z + txy = t + xyz = А, xyzt = B, тогда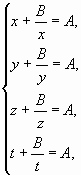 Û 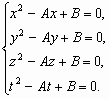Следовательно, числа x, y, z и t являются корнями одного и того же квадратного уравнения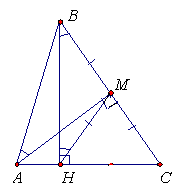 . Так как квадратное уравнение имеет не более двух корней, а по условию x > y и z > t, то x = z и y = t.

4.2. В треугольнике АВС медиана АМ равна высоте BH. Кроме того, равны углы МАВ и НВС. Докажите, что треугольник АВС – равносторонний.

Из условия задачи следует, что НМ – медиана прямоугольного треугольника BCH, проведенная к гипотенузе, следовательно, НМ = ВС = BM. Тогда треугольник ВМН – равнобедренный, значит, Ð МНВ = Ð НВС. Используя также, что Ð НВС = Ð МАВ (по условию), получим, что Ð МНВ = Ð МАВ.

Таким образом, отрезок ВМ виден из точек А и Н под одинаковыми углами, поэтому точки A, B, M и H лежат на одной окружности. Так как прямой угол АНВ – вписанный, то АВ – диаметр этой окружности, тогда вписанный угол АМВ – также прямой.

Следовательно, медиана AM треугольника ABC является также и его высотой, поэтому треугольник ABC – равнобедренный: AB = AC. Кроме того, равны прямоугольные треугольники АМС и ВНС (АМ = BH, угол С – общий). Следовательно, AС = BC. Таким образом, треугольник АВС – равносторонний, что и требовалось.

4.3. Найдите все натуральные числа, которые можно представить в виде суммы двух взаимно простых чисел, отличных от 1.

Ответ: все натуральные числа, кроме 1, 2, 3, 4 и 6.

Рассмотрим сначала нечетные числа. Очевидно, что числа 1 и 3 указанным способом представить нельзя. Пусть N – нечетное и N ³ 5. Тогда N = 2k + 1 = k + (k + 1), где k – натуральное и k ³ 2. Так как любые два последовательных натуральных числа взаимно просты, то все указанные N удовлетворяют условию.

Рассмотрим четные числа. Непосредственной проверкой убеждаемся, что числа 2, 4 и 6 нельзя представить в указанном виде. Остальные четные числа можно разбить на две группы: числа, кратные 4, то есть N = 4k, и числа, не кратные 4, то есть N = 4k + 2 (k – натуральное и k ³ 2).

В первом случае: N = 4k = (2k + 1) + (2k – 1), причем НОД(2k + 1; 2k – 1) = НОД(2k – 1; 2) = 1. Во втором случае: N = 4k + 2 = (2k + 3) + (2k – 1), причем НОД(2k + 3; 2k – 1) = НОД(2k – 1; 4) = 1.

Для нечетных чисел, начиная с 5, возможно также и другое представление, удовлетворяющее условию: если k ³ 2, то N = 2k + 1 = 2 + (2k – 1).