11 класс
Результаты | Решения (doc-файл) | Решения (pdf-файл)Первый тур (10 минут; каждая задача – 6 баллов).
1.1.
Решите неравенство: x + y2 +1.2. Верно ли, что в пространстве два угла с соответственно перпендикулярными сторонами либо равны, либо составляют в сумме 180° ?
1.3. В клетках квадратной таблицы 10´ 10 стоят ненулевые цифры. В каждой строчке и в каждом столбце из всех стоящих там цифр произвольным образом составлено десятизначное число. Может ли оказаться так, что из двадцати получившихся чисел ровно одно не делится на 3?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Функция f(x) принимает только положительные значения. Известно, что ![]() и при любых а и b
и при любых а и b ![]() . Найдите
. Найдите ![]() .
.
2.2. Внутри параллелограмма ABCD выбрана произвольная точка Р и проведены отрезки РА, РВ, РС и PD. Площади трех из образовавшихся треугольников равны 1, 2 и 3 (в каком-то порядке). Какие значения может принимать площадь четвертого треугольника?
2.3. На шахматной доске расставили n белых и n черных ладей так, чтобы ладьи разного цвета не били друг друга. Найдите наибольшее возможное значение n.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1.
Найдите наибольшее значение выражения x2y – y2x, если 0 < x < 1 и 0 < y < 1.3.2. На сторонах АВ, ВС и СА треугольника АВС отмечены точки С1, А1 и В1 соответственно так, что ВС1 = С1А1 = А1В1 = В1С. Докажите, что точка пересечения высот треугольника С1А1В1 лежит на биссектрисе угла А.
3.3. Найдите все пары натуральных чисел (а; b), для которых выполняется равенство: НОК(а; b) – НОД(а; b) = ![]() .
.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Найдите все неотрицательные решения системы уравнений: 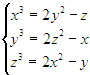 .
.
4.2. Вписанная окружность треугольника ABC касается его сторон ВС, АС и АВ в точках A', B' и C' соответственно. Точка K – проекция точки C' на прямую A'B'. Докажите, что KC' – биссектриса угла AKB.
4.3. В некотором государстве система авиалиний устроена таким образом, что любой город соединен авиалиниями не более, чем с тремя другими, и из любого города можно попасть в любой другой, сделав не более одной пересадки. Какое наибольшее количество городов может быть в этом государстве?
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. В классе находятся учитель и несколько учеников. Известно, что возраст учителя на 24 года больше среднего возраста учеников и на 20 лет больше среднего возраста всех присутствующих в классе. Сколько учеников находится в классе?
5.2. В тетраэдре ABCD плоские углы BAD и BCD – тупые. Сравните длины ребер AC и BD.
5.3. В шахматном турнире было 12 участников (каждый сыграл с каждым по одному разу). По итогам турнира оказалось, что есть 9 участников, каждый из которых набрал не более четырех очков. Известно, что Петя набрал ровно 9 очков. Как он сыграл с каждым из двух остальных шахматистов? (Победа – 1 очко, ничья – 0,5 очка, поражение – 0 очков.)
| Команда | I | II | III | IV | V | Итого | Диплом | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| 2 А | 5 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 9 | 9 | 7 | 7 | 103 | I | |
| СУНЦ А | 5 | 0 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 9 | 0 | 9 | 7 | 0 | 7 | 88 | II |
| 1543 Б | 4 | 6 | 6 | 7 | 7 | 7 | 8 | 0 | 8 | 9 | 0 | 9 | 7 | 0 | 7 | 85 | II |
| СУНЦ Б | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 5 | 1 | 0 | 0 | 7 | 7 | 7 | 82 | II |
| 5 Долгопрудный | 6 | 0 | 6 | 7 | 7 | 7 | 8 | 0 | 8 | 9 | 0 | 0 | 7 | 7 | 7 | 79 | III |
| Переславль | 4 | 0 | 6 | 5 | 6 | 7 | 8 | 8 | 0 | 9 | 9 | 9 | 7 | 1 | 0 | 79 | III |
| 218 А | 6 | 6 | 6 | 7 | 7 | 7 | 0 | 8 | 8 | 9 | 0 | 0 | 7 | 0 | 7 | 78 | III |
| 1514 Б | 4 | 6 | 6 | 7 | 7 | 2 | 8 | 0 | 8 | 9 | 0 | 0 | 7 | 7 | 7 | 78 | III |
| 2 В | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 7 | -1 | 0 | 9 | 7 | 0 | 0 | 77 | III |
| 218 Б | 6 | 6 | 6 | 7 | 7 | 7 | 2 | 0 | 8 | 9 | 0 | 9 | 0 | 0 | 7 | 74 | III |
| 1514 В | 6 | 6 | 6 | 7 | 7 | 2 | 0 | 8 | 8 | 9 | 0 | 0 | 7 | 0 | 7 | 73 | III |
| 315 А | 1 | 6 | 6 | 7 | 7 | 2 | 0 | 0 | 8 | 1 | 9 | 0 | 7 | 7 | 7 | 68 | пп |
| 2 Г | 0 | 6 | 6 | 7 | 6 | 2 | 8 | 0 | 8 | 7 | 0 | 2 | 7 | 0 | 7 | 66 | пп |
| 853 | 6 | 0 | 6 | 7 | 7 | 2 | 6 | 0 | 8 | 4 | 0 | 2 | 7 | 0 | 7 | 62 | пп |
| 1189 А | 6 | 0 | 6 | 3 | 0 | 7 | 8 | 0 | 0 | 9 | 0 | 9 | 7 | 0 | 7 | 62 | пп |
| 2007 А | 6 | 6 | 6 | 3 | 7 | 2 | 6 | 0 | 8 | 0 | 0 | 0 | 7 | 0 | 7 | 58 | пп |
| 218 В | 6 | 6 | 0 | 0 | 7 | 4 | 0 | 0 | 0 | 9 | 0 | 9 | 7 | 0 | 7 | 55 | пп |
| 1543 А | 0 | 6 | 6 | -1 | 7 | 7 | 4 | 0 | 8 | 1 | 0 | 9 | 7 | 0 | 0 | 54 | пп |
| 1514 А | 0 | 6 | 6 | 7 | 7 | 7 | 0 | 0 | 2 | 1 | 0 | 0 | 7 | 0 | 7 | 50 | пп |
| 54 А | 6 | 0 | 6 | 2 | 7 | 7 | 2 | 0 | 8 | 1 | 0 | 0 | 7 | 0 | 0 | 46 | |
| 444 А | 4 | 0 | 0 | 5 | 7 | 7 | 8 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 6 | 46 | |
| 1332 А | 5 | 0 | 6 | 0 | 7 | 7 | 8 | 0 | 4 | 9 | 0 | 0 | 0 | 0 | 0 | 46 | |
| 1581 А | 0 | 0 | 6 | 7 | 7 | 2 | 8 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 7 | 46 | |
| 30 С-Петербург | 6 | 0 | 6 | 2 | 7 | 2 | 0 | 0 | 0 | 7 | 0 | 0 | 7 | 0 | 7 | 44 | |
| 1151 А | 6 | 0 | 0 | 7 | 7 | 7 | 0 | 0 | 1 | 1 | 0 | 0 | 7 | 0 | 7 | 43 | |
| 1537 Б | 0 | 6 | 6 | 2 | 0 | 2 | 0 | 0 | 1 | 9 | 0 | 3 | 7 | 0 | 7 | 43 | |
| 1511 А | 6 | 0 | 6 | 3 | 7 | 2 | 8 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 40 | |
| 2007 Г | 4 | 0 | 6 | 5 | 4 | 2 | 8 | 0 | 4 | 0 | 0 | 7 | 0 | 40 | |||
| 2 Б | 4 | 1 | 0 | 0 | 4 | 0 | 1 | 0 | 0 | 9 | 0 | 5 | 7 | 0 | 7 | 38 | |
| 218 Г | 6 | 4 | 0 | 0 | 7 | 7 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 4 | 7 | 37 | |
| Троицк А | 0 | 0 | 6 | 0 | 0 | 2 | 8 | 0 | 0 | 5 | 0 | 0 | 7 | 0 | 7 | 35 | |
| 315 Б | 0 | 0 | 0 | 0 | 7 | 2 | 8 | 0 | 0 | 4 | 0 | 7 | 0 | 6 | 34 | ||
| 91 Б | 0 | 4 | 0 | 3 | 3 | 2 | 3 | 0 | 0 | 4 | 0 | 0 | 7 | 0 | 6 | 32 | |
| 1511 Б | 0 | 0 | 0 | 7 | 7 | 2 | 8 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 0 | 32 | |
| 1534 Б | 5 | 0 | 0 | 3 | 3 | 2 | 3 | 0 | 0 | 1 | 0 | 1 | 7 | 0 | 7 | 32 | |
| 2007 В | 6 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 7 | 0 | 7 | 30 | |
| 354 А | 0 | 1 | 0 | 1 | 0 | 7 | 8 | 0 | 0 | 2 | 0 | 0 | 7 | 0 | 0 | 26 | |
| 1840 А | 0 | 0 | 0 | 0 | 0 | 2 | 8 | 0 | 0 | 7 | 0 | 0 | 7 | 0 | 0 | 24 | |
| 2007 Б | 5 | 0 | 0 | 0 | 4 | 7 | 0 | 7 | 0 | 1 | 0 | 0 | 0 | 24 | |||
| 315 В | 0 | 0 | 0 | 7 | 2 | 2 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 0 | 19 | ||
| 1581 Б | 6 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 3 | 7 | 0 | 0 | 19 | |
| Троицк Б | 0 | 0 | 0 | 0 | 2 | 8 | 8 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 19 | ||
| 1189 Б | 5 | 0 | 0 | 0 | 7 | 2 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 | |
| 1332 Б | 0 | 0 | 0 | 0 | 7 | 2 | 0 | 0 | 0 | 2 | 0 | 0 | 7 | 0 | 0 | 18 | |
| 1537 А | 5 | 6 | 0 | 0 | 0 | 2 | 3 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 18 | |
| 444 Б | 4 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 0 | 17 | ||
| 1557 А | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 7 | 0 | 0 | 15 | |
| 1580 | 0 | 0 | 0 | 2 | 0 | 1 | 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 7 | 13 | |
| 7 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 0 | 12 | |
| 1564 А | 0 | 6 | 0 | 0 | 3 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 12 | |
| 25 | 0 | 0 | 0 | 0 | 7 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | ||
| 1564 Б | 6 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 10 | |
| 1590 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 0 | 10 | |
| 1151 Б | 0 | 0 | 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 6 | |||
| 1986 А | 0 | 0 | 0 | 3 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 6 | |
| 91 А | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | |
| 1212 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 4 | |
| 1534 А | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 4 | ||
| 354 Б | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | ||
| 1652 А | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |