11 класс
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Для каких значений x выполняется неравенство:Ответ: при n = 2 или n = 3.
Решение. Заметим, что n2 – 1 = (n + 1)(n – 1), а НОД(n + 1; n – 1) = d ≤ 2. Если d = 2, то n2 – 1 является степенью двойки, а если d = 1, то n2 – 1 – это первая степень простого числа. В первом случае >n + 1 = 2k и n - 1 = 2m, причем значения этих степеней различаются на 2. Значит, k = 2, m = 1, тогда n = 3. Во втором случае n – 1 = 1, то есть n = 2.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Существует ли такое значение α, что все члены бесконечной последовательности cosα; cos2α; ... ; cos(2n;α); ... принимают отрицательные значения? Ответ: да, существует. Пусть, например, α =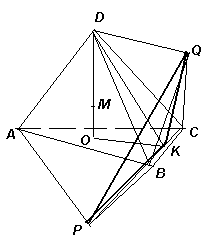 2.2. На каждой грани правильного тетраэдра с ребром 1 во внешнюю сторону построены правильные тетраэдры. Четыре их вершины, не принадлежащие исходному тетраэдру, образовали новый тетраэдр. Найдите его ребра.
Ответ: каждое ребро равно
2.2. На каждой грани правильного тетраэдра с ребром 1 во внешнюю сторону построены правильные тетраэдры. Четыре их вершины, не принадлежащие исходному тетраэдру, образовали новый тетраэдр. Найдите его ребра.
Ответ: каждое ребро равно 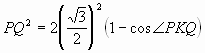 . Следовательно,
. Следовательно, 2.3. Может ли объединение двух треугольников оказаться 13-угольником?
Ответ: нет, не может. Решение. Пусть объединением двух треугольников является некоторый n- угольник. Докажем, что n ≤ 12. Действительно, вершинами n-угольника могут являться либо вершины исходных треугольников, либо точки попарного пересечения их сторон. Вершин у двух треугольников – 6. Каждая сторона одного треугольника не может пересечь более двух сторон другого, поэтому таких точек не более, чем 3× 2 = 6. Значит, всего вершин не более, чем 12. Отметим, что объединяя два треугольника, легко получить двенадцатиугольник. Именно так получается шестиконечная звезда.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Сумма восьми чисел равна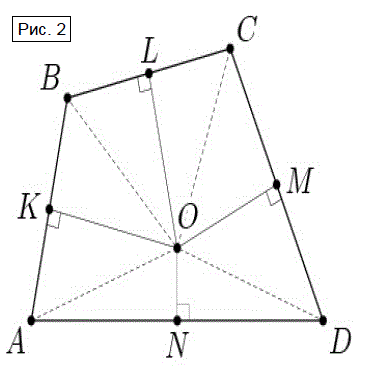 Из двух наклонных, проведенных из одной точки больше та, у которой проекция больше. Поэтому из неравенств, заданных в условии задачи, следует, что ОА ≥ OB ≥ OC ≥ OD ≥ OA. Значит, ОА = OB = OC = OD , то есть О – центр окружности, описанной около четырехугольника АВСD (см. рис. 2). Тогда точки K, L, M и N являются серединами сторон АВСD.
По теореме Вариньона (середины сторон четырехугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника) получим, что
Из двух наклонных, проведенных из одной точки больше та, у которой проекция больше. Поэтому из неравенств, заданных в условии задачи, следует, что ОА ≥ OB ≥ OC ≥ OD ≥ OA. Значит, ОА = OB = OC = OD , то есть О – центр окружности, описанной около четырехугольника АВСD (см. рис. 2). Тогда точки K, L, M и N являются серединами сторон АВСD.
По теореме Вариньона (середины сторон четырехугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника) получим, что Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Числа x, y, z и t лежат в интервале (0, 1). Докажите неравенство:![]() < 4 .
< 4 .
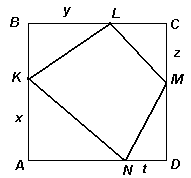 Второй способ. Рассмотрим квадрат ABCD со стороной 1. На его сторонах АВ, ВС, С D и DA отложим отрезки AK = x, BL = y, CM = z и DN = t соответственно (см. рис. 3).
Тогда требуемое неравенство примет вид NK + KL + LM + MN < 4. По неравенству треугольника: NK < AK + AN; KL < BK + BL; LM < CL + CM и MN < DM + DN. Сложив эти неравенства почленно, получим, что NK + KL + LM + MN < AB + BC + CD + DA = 4 .
Второй способ. Рассмотрим квадрат ABCD со стороной 1. На его сторонах АВ, ВС, С D и DA отложим отрезки AK = x, BL = y, CM = z и DN = t соответственно (см. рис. 3).
Тогда требуемое неравенство примет вид NK + KL + LM + MN < 4. По неравенству треугольника: NK < AK + AN; KL < BK + BL; LM < CL + CM и MN < DM + DN. Сложив эти неравенства почленно, получим, что NK + KL + LM + MN < AB + BC + CD + DA = 4 .
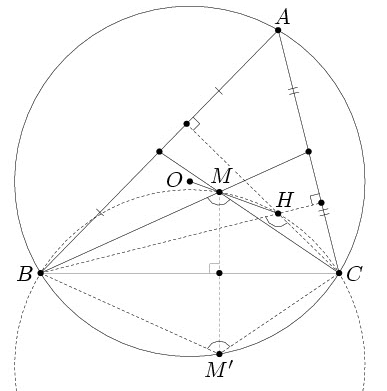 4.2. Известно, что в неравностороннем треугольнике ABC точка, симметричная точке пересечения медиан относительно стороны BC, принадлежит описанной окружности. Докажите, что ∠
BAC < 60°.
Пусть ∠BAC = α, М – точка пересечения медиан треугольника АВС, а точка М' симметрична ей относительно ВС (см. рис. 4). Тогда ∠BMC = ∠ BM'C = 180° – α.
Так как точка М лежит внутри треугольника АВС, то 180°
– α
> α
, то есть α
< 90°
. Следовательно, центр О окружности, описанной около треугольника АВС, лежит в одной полуплоскости с вершиной А (относительно ВС), поэтому ∠
BОC = 2α
.
Докажем, что О лежит вне окружности, описанной около треугольника ВМС. Действительно, если Н – ортоцентр треугольника, то ∠ВНС = 90° + ∠НBA = 180° – α = ∠BMC, значит, точка Н лежит на окружности, описанной около треугольника ВМС. Кроме того, точка М лежит на отрезке ОН (теорема о прямой Эйлера). Следовательно, точка О лежит вне окружности, описанной около треугольника ВМС.
Тогда ∠
BОC < ∠
B M C, то есть 2α
< 180°
– α
⇔
α
< 60°
.
В заключительной фазе решения использовано, что точки О, М и Н попарно различны, так как треугольник АВС – не равносторонний.
4.3. Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого из рыцарей ровно три врага, причём враги его друзей являются его врагами. При каких n такое возможно?
Ответ: при n = 4 или n = 6.
Из условия задачи следует, что рыцарей – не менее четырех. Заметим, что у рыцаря не может быть более двух друзей, иначе найдутся 4 рыцаря, у которых есть общий враг, но тогда у этого врага, в свою очередь, будет не менее четырех врагов, что противоречит условию. Значит, у каждого рыцаря не более двух друзей и ровно три врага, следовательно, всего рыцарей – не более шести.
Докажем, что не могло быть пяти рыцарей. Пусть рыцарей – 5: A , B , C , D и E . Тогда есть 2 рыцаря которые дружат между собой. Пусть A и B дружат, тогда C , D и E – их враги. Заметим, что C , D и E не могут попарно враждовать или попарно дружить, так как тогда у каждого из них либо по 4 врага, либо по 2. Если же дружат только двое, например, C и D , то у E – 4 врага, а если С дружит и с D, и с Е, то у него 2 врага. Оба случая невозможны, значит, рыцарей не может быть ровно 5.
4.2. Известно, что в неравностороннем треугольнике ABC точка, симметричная точке пересечения медиан относительно стороны BC, принадлежит описанной окружности. Докажите, что ∠
BAC < 60°.
Пусть ∠BAC = α, М – точка пересечения медиан треугольника АВС, а точка М' симметрична ей относительно ВС (см. рис. 4). Тогда ∠BMC = ∠ BM'C = 180° – α.
Так как точка М лежит внутри треугольника АВС, то 180°
– α
> α
, то есть α
< 90°
. Следовательно, центр О окружности, описанной около треугольника АВС, лежит в одной полуплоскости с вершиной А (относительно ВС), поэтому ∠
BОC = 2α
.
Докажем, что О лежит вне окружности, описанной около треугольника ВМС. Действительно, если Н – ортоцентр треугольника, то ∠ВНС = 90° + ∠НBA = 180° – α = ∠BMC, значит, точка Н лежит на окружности, описанной около треугольника ВМС. Кроме того, точка М лежит на отрезке ОН (теорема о прямой Эйлера). Следовательно, точка О лежит вне окружности, описанной около треугольника ВМС.
Тогда ∠
BОC < ∠
B M C, то есть 2α
< 180°
– α
⇔
α
< 60°
.
В заключительной фазе решения использовано, что точки О, М и Н попарно различны, так как треугольник АВС – не равносторонний.
4.3. Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого из рыцарей ровно три врага, причём враги его друзей являются его врагами. При каких n такое возможно?
Ответ: при n = 4 или n = 6.
Из условия задачи следует, что рыцарей – не менее четырех. Заметим, что у рыцаря не может быть более двух друзей, иначе найдутся 4 рыцаря, у которых есть общий враг, но тогда у этого врага, в свою очередь, будет не менее четырех врагов, что противоречит условию. Значит, у каждого рыцаря не более двух друзей и ровно три врага, следовательно, всего рыцарей – не более шести.
Докажем, что не могло быть пяти рыцарей. Пусть рыцарей – 5: A , B , C , D и E . Тогда есть 2 рыцаря которые дружат между собой. Пусть A и B дружат, тогда C , D и E – их враги. Заметим, что C , D и E не могут попарно враждовать или попарно дружить, так как тогда у каждого из них либо по 4 врага, либо по 2. Если же дружат только двое, например, C и D , то у E – 4 врага, а если С дружит и с D, и с Е, то у него 2 врага. Оба случая невозможны, значит, рыцарей не может быть ровно 5.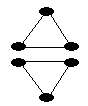 Примеры: если рыцарей – 4, то друзей ни кого из них нет и каждый враг каждому, а если рыцарей – 6, то разбиваем рыцарей на две тройки и каждый рыцарь дружит с рыцарями из своей тройки и враждует с рыцарями из другой.
Второй способ. Заметим, что из условия задачи следует, что отношение “быть другом” – транзитивно. Действительно, пусть А дружит с B , а B дружит с C, тогда А и C не могут быть врагами, так как в этом случае они должны быть врагами и для B. Значит, А и С – друзья.
Рассмотрим сначала граф, у которого n вершин, обозначающих рыцарей, а ребра соединяют пары врагов. Так как у каждого рыцаря ровно три врага, то n
Примеры: если рыцарей – 4, то друзей ни кого из них нет и каждый враг каждому, а если рыцарей – 6, то разбиваем рыцарей на две тройки и каждый рыцарь дружит с рыцарями из своей тройки и враждует с рыцарями из другой.
Второй способ. Заметим, что из условия задачи следует, что отношение “быть другом” – транзитивно. Действительно, пусть А дружит с B , а B дружит с C, тогда А и C не могут быть врагами, так как в этом случае они должны быть врагами и для B. Значит, А и С – друзья.
Рассмотрим сначала граф, у которого n вершин, обозначающих рыцарей, а ребра соединяют пары врагов. Так как у каждого рыцаря ровно три врага, то n
Пятый тур (15 минут; каждая задача – 7 баллов).
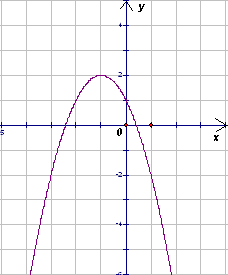 5.1. На координатной плоскости изображен график функции y = ax2 + bx + c (см. рисунок). На этой же координатной плоскости схематически изобразите график функции y = cx2 + 2bx + a . Ответ поясните.
5.1. На координатной плоскости изображен график функции y = ax2 + bx + c (см. рисунок). На этой же координатной плоскости схематически изобразите график функции y = cx2 + 2bx + a . Ответ поясните.
Ответ: см. рис. 6.
Вычислим значения a, b и c . Первый способ. Выберем три удобные точки данного графика, например, (0; 1); (1; –2) и (–1; 2). Учитывая, что y(0) = c; y(1) = a + b + c; y(–1) = a – b + c, получим систему уравнений: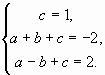 Ее решением является: a = – 1; b = – 2; c = 1.
Ее решением является: a = – 1; b = – 2; c = 1. 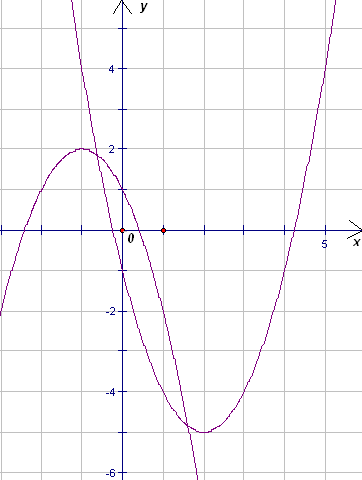 Второй способ. Заметим, что данный график получается параллельным переносом графика функции y = – x2 , поэтому a = – 1 . Значение b = – 2 вычисляется из равенства
Второй способ. Заметим, что данный график получается параллельным переносом графика функции y = – x2 , поэтому a = – 1 . Значение b = – 2 вычисляется из равенства 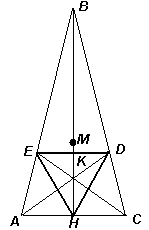 5.2. Верно ли, что в любом треугольнике точка пересечения медиан лежит внутри треугольника, образованного основаниями биссектрис?
5.2. Верно ли, что в любом треугольнике точка пересечения медиан лежит внутри треугольника, образованного основаниями биссектрис?
Ответ: нет, неверно.
Приведем один из возможных примеров. Рассмотрим равнобедренный треугольник АВС, в котором АВ = ВС = 3, АС = 1(см.рис. 7). Пусть ВН - его высота, АD и CE - биссектрисы, M - точка пересечения медиан. Тогда BE : EA = BD : DC = AB : AC = 3 : 1 (по свойству биссектрисы треугольника). Пусть отрезок DE пересекает ВН в точке K, тогда BK : KH = 3 : 1 ( по теореме о пропорциональных отрезках ) . BM : MH = 2 : 1 ( по свойству медиан треугольника). Следовательно, точка G лежит вне треугольника DEH , образованного основаниями биссектрис.
5.3. Найдите все трехзначные числа, квадраты которых оканчиваются на 1001.
Ответ: 501; 749. Первый способ. Пусть