10 класс

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Сумма трёх чисел равна нулю. Может ли сумма их попарных произведений быть положительной?

Ответ: нет, не может.

Решение. Пусть a +b +c = 0. Докажем, что ab + bc + ca ≤ 0.

Первый способ. Из условия задачи следует, что (a +b +c) ² = 0 ⇔ a² +b² +c² + 2( ab + bc + ca) = 0. Так как a² +b² +c² ≥ 0, то ab + bc + ca ≤ 0.

Второй способ. Из условия задачи следует, что с = –( а +b), тогда ab + bc + ca =ab + c( a +b) =ab – (а +b) ² = – (a² +ab +b²) ≤ 0, так как в скобках стоит неполный квадрат двучлена.

Следовательно, условие ab + bc + ca > 0 выполняться не может.

1.2. Дан треугольник со сторонами 3, 4 и 5. Построены три круга радиусами 1 с центрами в вершинах треугольника. Найдите суммарную площадь частей кругов, заключенных внутри треугольника.

Ответ: .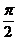

Решение. Из условия задачи следует, что построенные круги не пересекаются. Кроме того, высота данного прямоугольного треугольника, проведенная к гипотенузе, равна 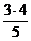> 1, значит, каждая часть круга, лежащая внутри треугольника, является сектором радиуса 1, центральный угол которого совпадает с углом треугольника. Так как сумма углов треугольника равна π, то суммарная площадь этих секторов равна площади половины единичного круга, то есть равна .

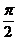1.3. Три трехзначных простых числа, составляющие арифметическую прогрессию, записаны подряд. Может ли полученное девятизначное число быть простым?

Ответ: нет, не может.

Решение. Первый способ. Так как данные простые числа составляют арифметическую прогрессию, то их можно записать в виде: а – d, а, а +d. Сумма цифр каждого из этих чисел дает тот же остаток при делении на 3, что и само число. Значит, сумма цифр девятизначного числа дает тот же остаток при делении на 3, что и сумма данных чисел, которая равна 3а. Таким образом, полученное число делится на 3, то есть оно не является простым.

Второй способ. Заметим, что разность прогрессии должна быть кратна трем, иначе три члена прогрессии будут иметь разные остатки от деления на 3, то есть среди них будет число, кратное трем, которое не может быть простым. Следовательно, данные числа имеют одинаковые остатки при делении на 3 и такие же остатки при делении на 3 имеют суммы их цифр, поэтому сумма цифр девятизначного числа кратна трем. Таким образом, полученное число делится на 3, то есть оно не является простым.

Ситуация, описанная в условии, возможна: например, записаны числа 107, 137, 167 или 167, 197, 227. Отметим также, что доказанное утверждение справедливо для любой тройки простых чисел, не обязательно трехзначных.

Второй тур (15 минут; каждая задача – 7 баллов).

2.1. Найдите 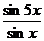, если .

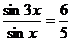Ответ: –0,76.

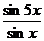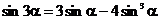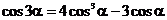Решение. 1) Преобразуем , используя формулы тройного аргумента ( и ), а также формулы синуса суммы и двойного аргумента: 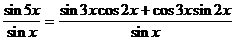= (3 – 4sin ²x)cos2 x + 2cos x(4cos ³x –3cos x) = (3 – 4sin ²x)(1 – 2sin ²x) + 8cos ⁴x – 6cos ²x = 3 – 4sin ²x – 6sin ²x + 8sin ⁴x + 8cos ⁴x – 6cos ²x = –3 – 4sin ²x + 8sin ⁴x + 8(1 – sin ²x) ² = –3 – 4sin ²x + 8sin ⁴x + 8 – 16sin ²x + 8sin ⁴x= 16sin ⁴x – 20sin ²x + 5.

2) Найдем значение sin ²x: 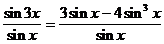= 3 – 4sin ²x; 3 – 4sin ²x = 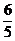⇔ sin ²x =.

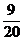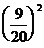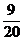3) Вычислим: 16sin ⁴x – 20sin ²x + 5 = 16 – 20 + 5 =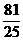 – 4 = – 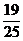= –0,76.

В пункте 1)фактически доказана формула:sin5x = 16sin ⁵x– 20sin ³x + 5sinx.

2.2. В прямоугольном параллелепипеде АВСDA’ B’ C’ D’ АВ =ВС =а, AA’ =b. Его ортогонально спроектировали на некоторую плоскость, содержащую ребро CD. Найдите наибольшее значение площади проекции.

Ответ: .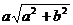

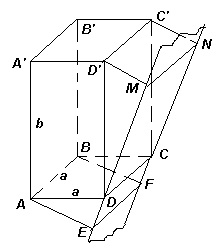
Решение. Пусть плоскость проекции a расположена так, как показано на рис. 1. Тогда проекция параллелепипеда совпадает с проекцией его диагонального сечения АВС’ D’. Так как площадь ортогональной проекции многоугольника не превосходит площади многоугольника, то площадь проекции будет наибольшей, если a параллельна этому сечению. В этом случае S_np = S_ABC'D' = AB * AD' = .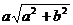

Если плоскость a содержит внутренние точки параллелепипеда, то его проекция совпадает с проекцией диагонального сечения A’ B’ CD. Так как площади диагональных сечений равны, то ответ не изменится.

Этот же результат можно получить непосредственным вычислением. ПустьMNFE –проекция параллелепипеда (см. рис. 1).Так как АВ|| CD,то АВ||α. Аналогично,C’D’||α, значит, искомая проекция состоит из двух прямоугольниковCDEFиCDMN, являющихся проекциями гранейABCDиCDD’C’соответственно. Пустьα составляет угол φ с плоскостью граниCDD’C’, тогда угол между ней и плоскостью грани АВСD равен 90°–φ. Тогда S_np = S_CDD'C'* cos φ + S_ABCD * cos (90° - φ) = ab cos φ + a² sin φ = a(a sin φ + b cos φ). Учитывая, что наибольшее значение выражения в скобках равно 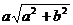, получим ответ.

2.3. Натуральные числа 1, 2, ..., 199, 200 разбили на 50 множеств. Всегда ли хотя бы в одном из множеств найдутся три числа, являющиеся длинами сторон какого-либо треугольника?

Ответ: всегда.

Решение. Рассмотрим все числа от 100 до 200. Для любых трех чисел из этого набора существует треугольник с такими длинами сторон. Так как в рассмотренном наборе – 101 число, то в каком-то из множеств разбиения окажутся хотя бы 3 числа из этого набора (принцип Дирихле).

Третий тур (20 минут; каждая задача – 8 баллов).

3.1. По положительным числам х и у вычисляют а = и b = y +. После этого находят С – наименьшее число из трех: x, a и b. Какое наибольшее значение может принимать C?

Ответ: .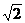

Решение. Из условия задачи следует, что С ≤ x, С ≤ а и С ≤ b. Так как b =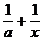, то С ≤ 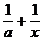. Кроме того, так как все числа – положительные, то 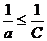и 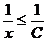. Таким образом, С ≤ 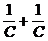, то есть С ≤ .

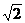Значение 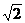достигается, если x = 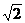, y = 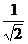, так как в этом случае а = 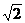и b = .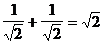

3.2. Четырехугольник ABCD вписан в окружность, АС =а, BD =b, AB⊥CD. Найдите радиус окружности.

Ответ: .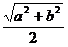

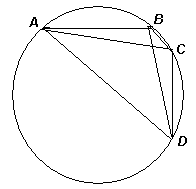
Решение. Пусть R – радиус окружности, ∠BAD = α, тогда, так как AB⊥ CD, то ∠CDА = 90° – α (см. рис. 2). По следствию из теоремы синусов BD = 2Rsin ∠BAD = 2Rsin α; AC = 2Rsin ∠CDА = 2Rcos α. Следовательно, BD² +AC² = 4R², значит, R = .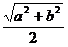

Отметим, что ответ не изменится, если концы хорд АВ и CD расположены на окружности в другом порядке, образуя четырехугольник АСBD с перпендикулярными диагоналями.

3.3. В турнире участвовало 11 шахматистов: 4 – из России и 7 зарубежных. Каждый шахматист сыграл с каждым по две партии (выигрыш – 1 очко, ничья – 0,5 очка, поражение – 0). По окончании турнира оказалось, что все участники набрали различное количество очков, причем сумма очков, набранных россиянами, равна сумме очков, набранных иностранцами. Могло ли в тройке призеров не оказаться ни одного россиянина?

Ответ: нет, не могло.

Решение. Количество партий, сыгранных в турнире, равно = 110. Очков было разыграно столько же, значит, как россияне, так и иностранцы в сумме набрали по 55 очков. Лучший из российских шахматистов не мог набрать меньше, чем 14,5 очков (иначе, сумма очков, набранных россиянами, не больше, чем 14 + 13,5 + 13 + 12,5 = 53 < 55). Пусть его опередили хотя бы трое иностранцев, тогда они набрали в сумме не меньше, чем 15 + 15,5 + 16 = 46,5 очков. Значит, четыре остальных зарубежных шахматиста набрали в сумме не больше, чем 55 – 46,5 = 8,5 очков. Но эти шахматисты только во встречах между собой разыграли = 12 очков, то есть сумма набранных ими очков не могла быть меньше, чем 12. Полученное противоречие показывает, что хотя бы один из россиян стал призером турнира.

Четвертый тур (25 минут; каждая задача – 9 баллов).

4.1. Найдите все строго возрастающие последовательности натуральных чисел a₁, a₂, …, a _n, ..., в которых a₂ = 2 и a _nm =a _na _m для любых натуральных n и m.

Ответ: а_n = n.

Решение. Так как a₁ < a₂ и a₁ – натуральное число, то a₁ = 1. Докажем теперь методом математической индукции, что .

1) База: 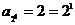. 2) Шаг индукции: пусть 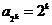, тогда .

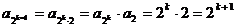Доказав, что 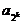, заметим: между и находится ровно 2^{k + 1} – 2^k – 1 = 2^k – 1 членов последовательности и столько же натуральных чисел. Учитывая также, что искомая последовательность (а_n) – строго возрастающая, получим, что для любых натуральных n должно выполняться равенство а_n = n.

В этом случае a _nm =nm =a _na _m для любых натуральных n и m.

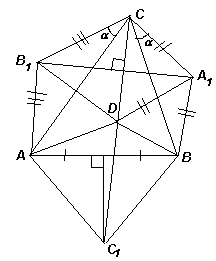
4.2. Дан неравнобедренный остроугольный треугольник АВС. Вне его построены равнобедренные тупоугольные треугольники АВ₁С и ВА₁С с одинаковыми углами a при их основаниях АС и ВС. Перпендикуляр, проведенный из вершины С к отрезку А₁В₁ пересекает серединный перпендикуляр к стороне АВ в точке С₁. Найдите угол АС₁В.

Ответ: 2a.

Решение. Заметим, что ∠АСВ + 2α < 90° + 2*45° = 180°, поэтому А₁В₁ пересекает стороны АС и ВС (см. рис. 3). Пусть точка D симметрична вершине С относительно А₁В₁, тогда D лежит на отрезке СС₁. Кроме того, А₁D =А₁B = А₁C.

В четырехугольнике А₁BDC: ∠ВА₁С = 180° – 2<α, ∠BDC = ∠А ₁BD + ∠А ₁CD =x, тогда 2x + 180° – 2α = 360°, значит, x = 90° + α. Аналогично, ∠ADC = 90° + α.

Следовательно, ∠ADC₁= ∠A₁DC₁= 90° – α, то есть DC₁ – биссектриса угла АDВ. Тогда точка С₁ пересечения биссектрисы треугольника АDВ и серединного перпендикуляра к стороне АВ лежит на окружности, описанной около этого треугольника. Таким образом, ∠АС₁В = 180° – ∠АDВ = 2a.

ТочкуDможно получить иначе. Рассмотрим окружности с центрами А ₁ и В ₁ и радиусами А ₁С и В ₁С соответственно. Так как точка С принадлежит обеим окружностям, а СС ₁ – перпендикуляр к их линии центров, тоD –вторая точка пересечения этих окружностей. В этом случае ∠BDC = 180° – 0,5 ∠BA ₁C = 90° +α (по теореме о вписанном и центральном углах).

4.3. Решите в целых числах уравнение (x² – y²) ² = 16 y + 1.

Ответ: (±1; 0), (±4; 3), (±4; 5).

Решение. Так как в правой части уравнения – нечетное число, то x² – y² = (x – y)( x + y) ? 0, то есть x – y ? 0 и x + y ? 0. Тогда (х + у) ² ≥ 1 и (х – у) ² ≥ 1. Следовательно, (x² – y²) ² ≥ (x + y) ² и (x² – y²) ² ≥ (x – y) ². Сложив два последних неравенства, получим: 2( x² – y²) ² ≥ (x + y) ² +( x – y) ² = 2x² + 2y². Следовательно, 2(16 y + 1) ≥ 2( x² +y²) ⇔ x² +y² – 16y ≤ 1 ⇔ x² + (y – 8) ² ≤ 65. Значит, 0 ≤ y ≤ 16. При этом, 16 y + 1 является полным квадратом, поэтому возможны только четыре значения y: 0, 3, 5, 14. Подставляя их в исходное уравнение, находим соответствующие целые значения x, если они существуют.

Пятый тур (15 минут; каждая задача – 7 баллов).

5.1. Найдите все натуральные n > 2, для которых многочлен x ⁿ + x² + 1 делится нацело на многочлен x² +x+ 1.

Ответ: n = 3k + 1, k∈N.

Решение. Рассмотрим различные остатки от деления n на 3:

1) Если n = 3k + 1 (k∈N), то x ⁿ +x² + 1 =x^{3 k +1} – x + x² +x + 1 =x( – 1) + (x² +x + 1) делится на x² +x+ 1, так как – 1 делится на x³ –1, а x³ –1 делится на x² +x + 1.

2) Если n = 3k + 2 (k∈N), то x ⁿ +x² + 1 =x^{3 k +2} – x² + 2x² + 1 = x²( – 1) + (2 x² + 1) не делится на x² +x+ 1, так как – 1 делится на x² +x + 1, а 2x² + 1 не делится на x² +x + 1.

3) Если n = 3k (k∈N), то x ⁿ +x² + 1 = ( – 1) + (x² + 2) не делится на x² +x+ 1, так как – 1 делится на x² +x + 1, а x² + 2 не делится на x² +x + 1.

Школьники, уже знакомые с комплексными числами, могли действовать по-другому: найти комплексные корни трехчлена x² +x+1, а затем, подставив их в многочлен xⁿ + x² + 1, потребовать, чтобы его значение равнялось нулю.

5.2. Существует ли непрямоугольный треугольник, вписанный в окружность радиуса 1, у которого сумма квадратов длин двух сторон равна 4?

Ответ: да, существует.

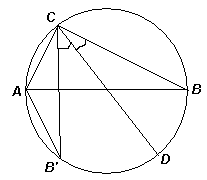
Решение. Первый способ. Пусть АВ = 2 – диаметр окружности, С – произвольная точка на окружности, тогда угол АСВ – прямой (см. рис. 4а). Проведем диаметр CD и отразим отрезок ВС относительно него. Тогда в непрямоугольном треугольнике АСВ’ получим, что AC² + B’ C² =AC² +BC² =АВ² = 4, что и требовалось.

Эту же идею решения можно реализовать, получив конкретный числовой пример. ПустьАС = 1, тогда ВС = 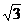,∠AB’C =∠ABC = 30°.Тогда из треугольника АСВ’ по теореме синусов: 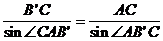, то естьsin ∠CAB’ = 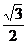. Учитывая, что этот угол – тупой, получим: ∠CAB’ = 120°, тогда ∠AСB’ =30° иAB’ = AC = 1. Тем самым, для решения задачи достаточно предъявить равнобедренный треугольник с боковой стороной 1 и углом при вершине 120°, вписанный в данную окружность.

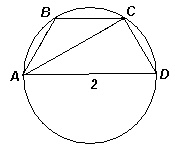
Второй способ. Впишем в данную окружность с диаметром AD = 2 трапецию АВСD. Так как трапеция – вписанная, то она – равнобокая. Проведем диагональ АС, тогда ∠ACD = 90° (см. рис. 4б). Тупоугольный треугольник АВС – искомый, так как AC² +AB² = АС² +CD² =AD² = 4.

И эту идею можно «конкретизировать», если выбрать точки В и С так, чтобыAB = BC = CD = 1, то есть, чтобы трапеция являлась «половиной» правильного вписанного шестиугольника. Тогда треугольник АВС – искомый, так как ∠ABC = 120°, АС = .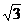

5.3. Прямоугольный параллелепипед размером m×n×k разбит на единичные кубики. Сколько всего образовалось параллелепипедов (включая исходный)?

Ответ: .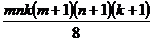

Решение. На трех ребрах данного параллелепипеда, исходящих из одной вершины, образовалось m + 1, n + 1 и k + 1 точка разбиения соответственно (включая концы). Далее можно рассуждать по-разному.

Первый способ. Каждый параллелепипед однозначно определяется тремя ребрами, исходящими из одной вершины. Количество возможных различных ребер по каждому из измерений равно количеству способов выбрать две точки из имеющихся, то есть оно равно 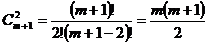; 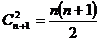и 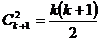соответственно.

Выбор ребра по каждому из измерений происходит независимо, поэтому искомое количество параллелепипедов равно × × = .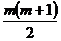

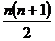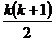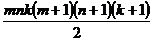Второй способ. Всего после разбиения в пространстве образуется (m + 1)( n + 1)( k + 1) точек, которые могут стать вершинами параллелепипедов. Заметим, что любые две точки, не лежащие в плоскости, параллельной одной из граней данного параллелепипеда, могут стать концами диагонали ровно одного из искомых параллелепипедов. Для каждой точки разбиения существует mnk точек, которые могут стать вторым концом такой диагонали, поэтому количество диагоналей равно 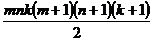. Но в каждом параллелепипеде – 4 диагонали, поэтому искомое количество параллелепипедов в 4 раза меньше, то есть оно равно .

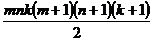Отметим, что можно провести аналогичные рассуждения, введя декартову систему координат в пространстве.