8 класс

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Вася сложил четвертую степень и квадрат некоторого числа, отличного от нуля, и сообщил результат Пете. Сможет ли Петя однозначно определить Васино число?

Ответ: нет, не сможет.

Решение. Предположим, что Вася выбрал число 1. Так как 1⁴ + 1² = 2, то результат, который он сообщит Пете – число 2. Но то же самое число 2 он сообщит Пете, если задумает число -1, поскольку (-1) ⁴ + (-1) ² = 2.

Так как равенство (-а) ² + (-а) ⁴ = а ² + а ⁴ справедливо для любого а, то какое бы число Вася изначально не выбрал, Петя его определить не сможет.

1.2. В прямоугольном треугольнике АВС проведена высота СН из вершины прямого угла. Из вершины В большего острого угла проведен отрезок BK так, что ∠ CBK = ∠ CАB (см. рисунок). Докажите, что СН делит BK пополам.

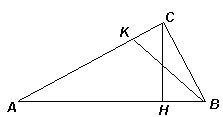
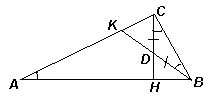
Решение. Пусть отрезки СН и BK пересекаются в точке D (см. рис. 1). Так как ∠ BСН = ∠ CАB = ∠ CBK, то треугольник BCD – равнобедренный: CD =BD. Тогда CD – медиана прямоугольного треугольника BCK, то есть BD =KD.

Заключительный вывод можно также сделать из того, что равны углы KCD и CKD (они дополняют равные углы до прямого), поэтому СD =KD.

1.3. По окончании шахматного турнира Незнайка сказал: «Я набрал на 3,5 очка больше, чем потерял». Могут ли его слова быть правдой? (Победа – 1 очко, ничья – 1/2очка, поражение – 0.)

Ответ: нет, не могут.

Решение. Первый способ. Пусть Незнайка потерял x очков, а набрал x + 3,5. Так как сумма набранных и потерянных очков равна количеству сыгранным им партий, то 2x + 3,5 должно быть целым числом, то есть 2x + 3,5 =N. Тогда 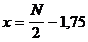, то есть дробная часть числа x равна 0,25 или 0,75, что невозможно (в реальности дробная частьx может быть равна только нулю или 0,5).

Второй способ. Перед началом турнира разность между набранными и потерянными очками равнялась нулю. Если партия результативна, то эта разность изменяется на 1, а если партия закончилась вничью, то разность не изменяется. Следовательно, такая разность может принимать только целые значения, то есть не может быть равна 3,5.

Второй тур (15 минут; каждая задача – 7 баллов).

2.1. Упростите выражение (избавьтесь от как можно большего количества знаков корней): .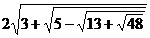

Ответ: + .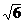

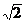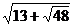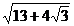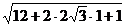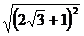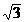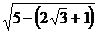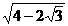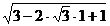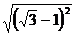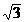Решение. 1) = = = = 2 + 1; 2) = = = = – 1; 3) = = = = + .

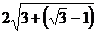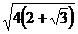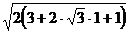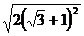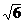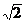2.2. Бумажный прямоугольный треугольник АВС перегнули по прямой так, что вершина С прямого угла совместилась с вершиной В и получился четырехугольник. В каких отношениях точка пересечения диагоналей четырехугольника делит эти диагонали?

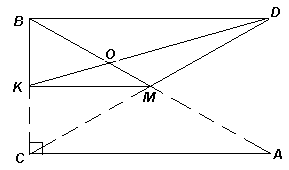
Ответ: обе диагонали – в отношении 2 : 1.

Решение. Из условия задачи следует, что линия сгиба – серединный перпендикуляр к отрезку ВС. Пусть этот перпендикуляр пересекает стороны ВС и АВ в точках K и М соответственно, тогда после перегибания получен четырехугольник BKMD, диагонали которого пересекаются в точке О (см. рис. 2). Далее можно рассуждать по-разному.

Первый способ. ВМ и DK – медианы треугольника ВСD, O – точка их пересечения, значит, ВО :ОМ =DO :OK = 2 : 1.

Второй способ. Так как KM – средняя линия треугольника АВС, то KM|| AC || BD и KM = 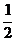AC = 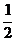BD. Значит, BKMD – трапеция, поэтому треугольники KOM и BOD подобны. Следовательно, ВО :ОМ =DO :OK =BD :KM = 2 : 1.

2.3. В клетках таблицы 3x3 расставили цифры от 1 до 9. Затем нашли суммы цифр в каждой строке. Какое наибольшее количество из этих сумм может оказаться полным квадратом?

Ответ: две.

3	1	5
2	6	8
4	9	7

Решение. Наименьшая возможная сумма цифр в строке: 1 + 2 + 3 = 6, а наибольшая: 7 + 8 + 9 = 24. Значит, если сумма является полным квадратом, то она должна быть равна 9 или 16. Предположим, что в каждой строчке таблицы сумма равна 9 или 16, тогда сумма всех цифр в таблице равна 9 + 9 + 9 = 27 или 9 + 9 + 16 = 34 или 9 + 16 + 16 = 41 или 16 + 16 + 16 = 48. Но сумма чисел от 1 до 9 равна 45, то есть трех сумм – полных квадратов быть не может.

Две такие суммы возможны, например, см. таблицу:

Отметим, что в этом примере полными квадратами являются суммы как в первых двух строчках, так и в первых двух столбцах.

Третий тур (20 минут; каждая задача – 8 баллов).

3.1. Набор из нескольких чисел, среди которых нет одинаковых, обладает следующим свойством: среднее арифметическое каких-то двух чисел из этого набора равно среднему арифметическому каких-то трех чисел из набора и равно среднему арифметическому каких-то четырех чисел из набора. Каково наименьшее возможное количество чисел в таком наборе?

Ответ: 5 чисел.

Решение. Условию задачи удовлетворяют числа 1, 2, 3, 4, 5. Действительно, 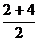= = 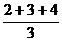= 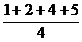3. Докажем, что четыре числа в наборе быть не может.

Пусть 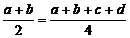, тогда a +b =c +d. Далее достаточно рассмотреть два случая:

1) В рассматриваемых наборах из двух и трёх чисел совпали два числа, то есть 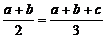. Тогда a +b = 2c. С учетом условия, полученного ранее, 2c =c +d, то есть c =d, что противоречит условию (числа должны быть различны).

2) В рассматриваемых наборах из двух и трёх чисел совпало одно число, то есть 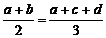. Тогда a + 3b = 2c + 2d. С учетом условия, полученного ранее, a + 3b = 2a + 2b, то есть а =b, что также противоречит условию.

Существуют и другие примеры.

3.2. В треугольнике ABC на сторонах AB, AC и BC выбраны точки D, E и F соответственно так, что BF = 2CF, CE = 2AE и угол DEF – прямой. Докажите, что DE – биссектриса угла ADF.

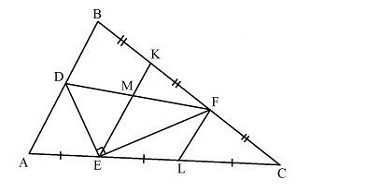
Решение. Первый способ. Через точки Е и F проведем прямые, параллельные АВ. Пусть они пересекают ВС и АС в точках K и L соответственно (см. рис. 3а). По теореме Фалеса K – середина отрезка BF, L – середина отрезка CE. Отметим точку M пересечения KE и DF, тогда, также по теореме Фалеса, M – середина отрезка DF.

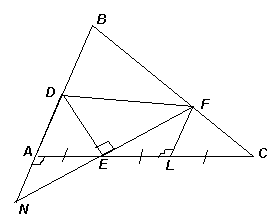
Таким образом, ЕМ – медиана прямоугольного треугольника DEF, проведенная к гипотенузе, поэтому МЕ =MD. Следовательно, ∠ MDE = ∠ MED. Кроме того, из параллельности прямых МЕ и AD следует, что ∠MED =∠EDA. Значит, ∠ ADE = ∠ FDE, то есть DE – биссектриса угла ADF.

Второй способ. Пусть прямая, проходящая через точку F и параллельная АВ, пересекает АС в точке L (см. рис. 3б). Тогда, по теореме о пропорциональных отрезках, AL = 2LC. Значит, Е – середина отрезка AL. Продлим FE до пересечения с прямой АВ в точке N. Из равенства треугольников АЕN и LEF (по стороне и прилежащим к ней углам) следует, что NE =FE. Тогда в треугольнике NDF отрезок DE является высотой и медианой, значит, этот треугольник – равнобедренный. Следовательно, DE – биссектриса угла ADF.

3.3. На доске выписаны числа 1, 2, …, 100. На каждом этапе одновременно стираются все числа, не имеющие среди нестертых чисел делителей, кроме себя самого. Например, на первом этапе стирается только число 1. Какие числа будут стерты на последнем этапе?

Ответ: 64 и 96.

Решение. На следующем этапе после стирания единицы будут стерты все простые числа (так как у них нет делителей, кроме 1 и самого числа). Далее будут стерты числа, в разложение которых входит ровно 2 простых множителя (необязательно различных), затем стерты числа, в разложение которых входит ровно 3 простых множителя, и так далее. Так как 2⁷ > 100, то среди заданных нет чисел, в разложение которых входит больше шести простых множителей. Следовательно, на последнем шаге будут стерты числа, в разложение которых входит ровно 6 простых множителей. Так как 3² x 2 ⁴ > 100, то таких чисел всего два: 2⁶ = 64 и 3 x 2 ⁵ = 96.

Четвертый тур (25 минут; каждая задача – 9 баллов).

4.1. Три числа x, y и z отличны от нуля и таковы, что x² – y² =yz и y² – z² =xz. Докажите, что x² – z² =xy.

Решение. Заметим, что |x| ≠ |y| и |y| ≠ |z| (иначе среди данных трех чисел есть нули). Сложив почленно два равенства из условия, получим: x² – z² =yz +xz, поэтому достаточно доказать, что yz +xz =xy.

Так как z ≠ 0, то из второго равенства в условии следует, что 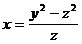. Подставив это значение x в первое равенство, получим: 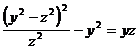⇔ 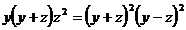Учитывая, что |y| ≠ |z|, далее получим: ⇔ .

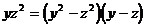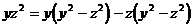Почленно разделим обе части последнего равенства на z, тогда: 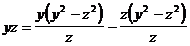⇔ yz =xy – xz, то есть xz +yz =xy, что и требовалось.

4.2. В параллелограмме ABCDO – точка пересечения диагоналей. Точка M лежит на продолжении стороны AB за точку B. Известно, что угол AMO равен углу ВAD. Докажите, что MC = MD.

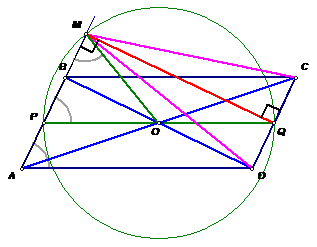
Решение. Первый способ. Заметим, что доказываемое утверждение равносильно тому, что точка М лежит на серединном перпендикуляре к отрезку CD (см. рис. 4а).

Рассмотрим отрезок PQ, проходящий через середины сторон АВ и CD соответственно. Так как PQ ||AD и PO =OQ, то ∠ MPO = ∠ BAD = ∠ PMO, то есть МО = РО.

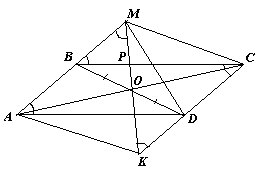
Таким образом, точка О – центр окружности, описанной около треугольника РМQ, PQ– диаметр этой окружности, значит, ∠ PMQ = 90°. Так как CD ||PM, то МQ^ CD. Учитывая, что Q –середина CD, получим требуемое.

Второй способ. Пусть прямая МО пересекает прямые ВС и CD в точках Р и K соответственно (см. рис. 4б). Тогда треугольники KOD и МОВ равны (по стороне и двум прилежащим углам). Следовательно, KD =MB.

Так как ∠ MBC = ∠ BAD = ∠ AMO, то треугольник ВМР – равнобедренный: ВР =MP. Так как ∠ MKC = ∠ AMK = ∠ BAD = ∠ BCD, то треугольник KCP – также равнобедренный: CР =KP. Следовательно, MK =BC.

Таким образом, равны треугольники MKD и СВМ (MK =BC, KD =MB, ∠ MKD = ∠ MBC), значит MD = MC.

Эту же идею решения можно реализовать по-другому. Заметим, что точки М и К симметричны относительно точки О – центра симметрии данного параллелограмма, значит отрезки СМ иAKтакже симметричны относительно О (см. рис. 4б). Тогда, доказав, чтоMK =BC =AD, получим, что в трапеции АМDKравны диагонали. Следовательно, эта трапеция – равнобокая, то есть МD =AK =MC.

4.3. В ряд записаны 20 различных натуральных чисел. Произведение любых двух чисел, стоящих подряд, является квадратом натурального числа. Первое число равно 42. Докажите, что хотя бы одно из чисел больше, чем 16000.

Решение. Заметим, что 42 = 2x3x7, то есть все простые множители – в первой степени. Следовательно, чтобы произведение первых двух чисел являлось полным квадратом, второе число должно иметь вид 42 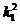, где k₁ – натуральное число.

Так как произведение второго и третьего числа – полный квадрат, то третье число, по тем же причинам, имеет вид 42 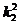, где k₂ – натуральное число, и так далее. Таким образом, все записанные числа, кроме первого, имеют вид 42 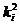, где k _i – натуральное число, отличное от единицы. Так как все числа различны, то наибольшее из чисел k _i не может быть меньше, чем 20. Следовательно, одно из записанных чисел не меньше, чем 42x20² > 16000.