10 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. На координатной плоскости изобразите множество точек, удовлетворяющих неравенству: 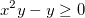
1.2. В выпуклом четырехугольнике тангенс одного из углов равен числу m. Могут ли тангенсы каждого из трех остальных углов также равняться m?
1.3. Можно ли поставить в ряд все натуральные числа от 1 до 100 так, чтобы любые два соседних числа отличались или на 2, или в два раза?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. (sinx, siny, sinz) – возрастающая арифметическая прогрессия. Может ли последовательность (cosx, cosy, cosz) также являться арифметической прогрессией?
2.2. Диагонали четырехугольника АВСD пересекаются в точке О, М и N – середины сторон ВС и AD соответственно. Отрезок MN делит площадь четырехугольника пополам. Найдите отношение ОМ : ОN, если AD = 2BC.
2.3. Число 1047 при делении на A дает остаток 23, а при делении на A + 1 – остаток 7. Найдите A.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Пусть a, b, c, d – действительные числа, удовлетворяющие системе равенств: 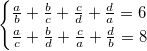
Какие значения может принимать выражение 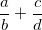 ?
?
3.2. Все грани треугольной пирамиды SABC – остроугольные треугольники. SX и SY – высоты граней ASВ и BSС. Известно, что четырехугольник AXYC – вписанный. Докажите, что прямые AC и BS перпендикулярны.
3.3. Кодовый замок откроется, если в каждой клетке квадрата размером 4×4 набрать число от 1 до 16 (не повторяясь) так, чтобы сумма чисел в каждом квадрате 2×2 была кратна 17. Можно ли открыть такой замок?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Сто положительных чисел записаны по кругу. Квадрат каждого числа равен сумме двух чисел, стоящих за этим числом по часовой стрелке. Какие числа могут быть записаны?
4.2. Трапеция с основаниями AD и BC описана вокруг окружности, E – точка пересечения ее диагоналей. Докажите, что угол AED – тупой.
4.3. В правильном 21-угольнике 6 вершин покрашены красным цветом, а 7 вершин – синим. Обязательно ли найдутся два равных треугольника, один из которых с красными вершинами, а другой – с синими?
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Решите уравнение: 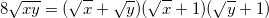
5.2. Две окружности пересекаются в точках А и В. Через точку В проведена прямая, пересекающая окружности в точках М и N так, что АВ – биссектриса треугольника МАN. Докажите, что отношение отрезков ВМ и BN равно отношению радиусов окружностей.
5.3. Какие значения может принимать наибольший общий делитель натуральных чисел m и n, если известно, что при увеличении числа m на 6 он увеличивается в девять раз?