VI СОРОСОВСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ.

ПЕРВЫЙ (ЗАОЧНЫЙ) ТУР

Внимание! В задаче N 6 по математике для 10 класса найдена и исправлена опечатка.

Дорогие юные друзья!

Международная Соросовская Программа Образования в Области Точных Наук (ISSEP) приглашает Вас принять участие в VI Соросовской олимпиаде школьников по математике, биологии, физике и химии.

В прошлом, 1998/99 учебном году после проведения заочного, очного и финального туров дирекция Олимпиады получила для проверки 281000 тетрадей школьников из всех регионов России, многих стран СНГ и ближнего зарубежья. 11700 школьников из 2400 школ 81 региона России, а также Украины, Белоруссии, Молдавии, Казахстана, Киргизии, Грузии, Армении и Эстонии были допущены к участию в финальном туре Олимпиады. Финальный тур проходил одновременно в 90 городах России и других стран. Победителями Олимпиады стали 733 школьника.

Организаторы всегда стремятся устроить Олимпиаду как праздник ярких идей, открытый и доступный для всех желающих. Структура проведения Олимпиады предоставляет возможность любому школьнику вне зависимости от территориальных делений и национальных границ принимать в ней участие, и только благодаря собственным успехам он может далее подниматься по ее крутым ступеням.

Олимпиада этого года по традиции начинается с проведения заочного тура по математике (для 7, 8, 9, 10,11-х классов), биологии и химии (9, 10 и 11-х классов), физике (для 10-х и 11-х классов). Участник может выполнять задания за класс, в котором он учится в 1999/2000 учебном году, или за старшие классы (требования к решениям одинаковы независимо от возраста). Участник Соросовской олимпиады может соревноваться по одному или нескольким предметам. Решения заданий по каждому предмету или классу будут проверяться и оцениваются отдельно, поэтому они должны содержаться в отдельных тетрадях. Результаты проверки высылаются участникам в школы. Решения задач будут опубликованы.

Правила оформления работ заочного тура

Решения задач должны быть представлены на русском языке в обыкновенной школьной тетради в клетку. На обложке напишите печатными буквами свою фамилию, класс и предмет, по которому выполнена работа.
На первой (белой) странице тетради (за обложкой) напишите печатными буквами разборчиво без сокращений:

1) название предмета, по которому выполнена работа;
2) класс, за который выполнена работа;
3) вашу фамилию, имя, отчество;
4) номер школы или юридическое название школы, в которой вы учитесь;
5) полный адрес школы с индексом;
6) телефон школы с кодом города;
7) полный домашний адрес с индексом;
8) домашний телефон с кодом города;
9) фамилию, имя, отчество вашего учителя по данному предмету.

Внимание! В случае нарушения правил оформления или неразборчивого почерка мы не можем гарантировать, что ваша работа будет проверена.

На второй странице (оборот первый) обязательно выпишите все ответы по всем решенным задачам в порядке их следования в задании. Если вы не решали задачу, то против ее номера поставьте прочерк. Если ответ в задаче выносить не следует, об этом сказано в ее условии.

Условия задач переписывать не нужно. Решение каждой задачи следует писать в порядке ее следования в задании, начиная с третьей страницы. Решение каждой задачи желательно поместить на одном листе (оно должно быть лаконичным, но без ущерба для полноты изложения). Решение каждой задачи начинайте с новой страницы.

Работы заочного тура необходимо выслать почтой не позднее 13 декабря 1999 года (для отдаленных районов 20 декабря) по адресу: 117234, Москва, а/я 590, "Олимпиада".

Желаем успехов!

Уважаемые руководители школ и учителя!

За пять лет Соросовские олимпиады собрали более 700000 участников из всех регионов России, многих стран СНГ и ближнего зарубежья. Система организации олимпиад совершенствуется год от года, обеспечивая соблюдение принципа максимальной доступности: двери, ведущие на Олимпиаду, всегда широко открыты для всех желающих в ней участвовать. Но никакая самая отлаженная система управления не смогла бы воплотить в жизнь принципы Соросовской олимпиады, если бы они не были востребованы и не нашли масштабной поддержки образовательного сообщества.

Дирекция Международной Соросовской Образовательной Программы считает необходимым выразить глубокую благодарность всем руководителям и работникам департаментов образования, директорам и учителям школ, родителям школьников, приложившим немало усилий для того, чтобы сотни тысяч школьников смогли проявить свои знания и способности, поверить в свои силы и в конечном итоге выбрать свой путь в жизни.

VI Соросовская олимпиада школьников по традиции начинается с проведения заочного тура. Мы надеемся, что задания этого тура станут доступными для учащихся вашей школы и они вместе с десятками тысяч школьников России и других стран получат возможность попробовать свои силы в Олимпиаде. После подведения итогов первого (заочного) тура планируется проведение второго (очного) тура во многих школах России и других странах.

Дирекция Соросовской олимпиады предлагает организовать проведение второго (очного) тура на базе вашей школы.

Заявку на проведение второго (очного) тура в вашей школе с указанием ее адреса и телефона, подписанную директором или другим должностным лицом и заверенную печатью школы, просим послать по почте в адрес дирекции (указан выше) не позднее 22 ноября 1999 года.

Даты проведения, регламент и задания второго тура в случае вашего согласия будут высланы в ваш адрес заказным письмом или доставлены нашим представителем заблаговременно.

Телефон для справок: (095) 939-39-45, 939-45-03

Факс (095) 939-47-85

E-mail: оlymp@issep.rssi.ru

С уважением,
директор программы "Соросовская олимпиада школьников" Б. И. Миропольский

Условия задач

МатематикаФизикаХимияБиология
7 класс
8 класс
9 класс9 класс9 класс
10 класс10 класс10 класс10 класс
11 класс11 класс11 класс11 класс

Математика

Математика. 7 класс.

1. Города A, B, C, D и E расположены друг за другом по шоссе на расстоянии 5 км друг от друга. Автобус курсирует по шоссе от города A до города E и обратно. Автобус расходует 20 литров бензина на каждые 100 километров. В каком городе кончится бензин у автобуса, если вначале в его баке было 150 литров бензина?

2. Найдите минимальное четырехзначное число, произведение всех цифр которого равно 729. Ответ объясните.

3. На параде солдаты выстроены в две шеренги одинаковой длины, причем в первой шеренге расстояние между соседними солдатами на 20% больше, чем во второй (между соседними солдатами в одной шеренге одинаковое расстояние). Сколько солдат в первой шеренге, если во второй шеренге 85 солдат?

4. Про три числа известно, что сумма любых двух из них не меньше удвоенного третьего числа, а сумма всех трех равна 300. Найдите все тройки таких (не обязательно целых) чисел.

5. Турист набирает два бака воды, используя два шланга. Из первого шланга в минуту вытекает 2,9 литров воды, из второго - 8,7 литров. В тот момент, когда меньший бак наполнился до половины, турист поменял шланги местами, после чего оба бака заполнились одновременно. Какова емкость большего бака, если емкость меньшего - 12,5 литров?

6. Можно ли на плоскости отметить 6 точек и соединить их непересекающимися отрезками (с концами в этих точках) так, чтобы из каждой точки выходило ровно по четыре отрезка?

7. Петя написал все натуральные числа от 1 до 1000 и обвел в кружочек те из них, которые представляются в виде разности квадратов двух целых чисел. Каких чисел среди обведенных больше - четных или нечетных?

8. На листе бумаги "в клетку" нарисуйте окружность максимального радиуса, пересекающую линии сетки только в узлах. Ответ объясните.

9. Вдоль железной дороги стоят километровые столбы на расстоянии 1 км друг от друга. Один из них покрасили в желтый цвет и шесть - в красный. Сумма расстояний от желтого столба до всех красных равна 14 км. Чему может быть равно максимальное расстояние между красными столбами?

10. Островное государство расположено на 100 островах, соединенных мостами, причем некоторые острова соединены мостом и с материком. Известно, что с каждого острова можно проехать на каждый (возможно, через другие острова). В целях повышения безопасности движения на всех мостах было введено одностороннее движение. Оказалось, что с каждого острова можно уехать только по одному мосту и что хотя бы с одного из островов можно уехать на материк. Докажите, что с каждого острова можно доехать до материка, причем по единственному маршруту.

Математика. 8 класс.

1. Может ли число, оканчивающееся на 1999, быть квадратом натурального числа?

2. Трехголовый Змей Горыныч праздновал свой день рождения. Его головы по очереди лакомились именинными пирогами и за 15 минут съели два одинаковых пирога. Известно, что каждая голова ела столько времени, сколько понадобилось бы двум другим, чтобы вместе съесть один такой же пирог. За сколько минут три головы Змея Горыныча съели бы вместе один пирог?

3. Найдите сумму коэффициентов многочлена, полученного после раскрытия скобок и приведения подобных членов в выражении:

а) (7x - 6)4 - 1; б) (7х - 6)1999 - 1.

4. Генерал хочет расположить семь зенитных установок так, чтобы среди любых трех из них нашлось две установки, расстояние между которыми ровно 10 километров. Помогите генералу решить эту задачу.

5. Гулливер, рост которого равен 999 лилиметров, строит башню из кубиков. Первый кубик имеет высоту 1/2 лиликилометра, второй - 1/4 лиликилометра, третий - 1/8 лиликилометра и т. д. Сколько кубиков будет в башне, когда ее высота превысит рост Гулливера. (1 лиликилометр равен 1000 лилиметров).

6. Известно, что в любом пятиугольнике можно выбрать три диагонали, из которых можно составить треугольник. Существует ли пятиугольник, в котором такие диагонали можно выбрать единственным способом.

7. Известно, что для натуральных чисел a и b выполняется равенство 19a = 99b. Может ли a + b быть простым числом?

8. Витя задумал 5 целых чисел и сообщил Ване все их попарные суммы:

0, 1, 5, 7, 11, 12, 18, 24, 25, 29.

Помогите Ване отгадать задуманные числа.

9. В квадрате 3*3 расставлены числа так, что суммы чисел в каждой строке, в каждом столбце и на каждой большой диагонали равны 0. Известно, что сумма квадратов чисел верхней строки равна n. Чему может быть равна сумма квадратов чисел нижней строки?

10. На окружности отмечено N точек. Два игрока играют в такую игру: первый игрок соединяет две из этих точек хордой, из конца которой второй игрок проводит хорду в одну из оставшихся точек так, чтобы не пересечь уже проведенную хорду. Затем такой же "ход" делает первый игрок - проводит из конца второй хорды новую хорду в одну из оставшихся точек так, чтобы она не пересекала ни одну из уже проведенных. Проигрывает тот, кто не может сделать такой "ход". Кто выигрывает при правильной игре? (Хордой называется отрезок, концы которого лежат на данной окружности)

Математика. 9 класс.

Примечание: в целях максимальной совместимости с различными программами просмотра html-страниц в условиях некоторых задач по математике радикалы n-й степени заменены на возведение в степень 1/n.

1. В телевизионной передаче "Поле чудес" ведущий разыгрывал приз следующим образом. Играющему показывали три шкатулки, в одной из которых находился приз. Играющий указывал на одну из шкатулок, после чего ведущий открывал одну из двух других оставшихся шкатулок, которая оказывалась пустой. После этого играющий мог либо настаивать на первоначальном выборе, либо сменить его и выбрать третью шкатулку. В каком случае его шансы на выигрыш возрастают? (Возможны три варианта ответа: обе шкатулки равноправны, лучше сохранить первоначальный выбор, лучше его изменить. Попытайтесь обосновать свой ответ.)

2. Найдите наименьшее натуральное n такое, что при всех целых m > n найдутся целые положительные x и y, для которых имеет место равенство

17x + 23y = m.

3. Найдите x + y, если

(x+(x2+1)1/2)(y+(y2+1)1/2) = 1.

4. На единичном отрезке расположено несколько непересекающихся отрезков красного цвета, общая длина которых больше 0,5. Обязательно ли найдутся две красные точки на расстоянии: а) 1/99; б) 1/100 ?

5. Угол А в треугольнике АВС равен a. Окружность, проходящая через А и В и касающаяся ВС , пересекает медиану к стороне ВС (или ее продолжение) в точке М, отличной от А. Найдите угол ВМС.

6. При всех допустимых значениях a и b упростите выражение

((4b-a2+2ab+4)1/2+a)/((4ab-10b2-8)1/2+b)

7. На прямой l расположены точки А, B, C и D так, что

(AB/BC)=(AC/CD)=l . Некоторая окружность касается прямой l в точке С. Через A проведена прямая, пересекающая эту окружность в точках M и N таких, что серединные перпендикуляры к отрезкам BM и DN пересекаются в точке Q на прямой l. В каком отношении точка Q делит отрезок AD?

8. На плоскости даны прямая l и луч р с началом на этой прямой. Построены две фиксированные окружности (не обязательно равные), вписанные в два образовавшихся угла. На луче р берется точка А так, что касательные из А к заданным окружностям, отличные от р, пересекают прямую l в точках В и С и при этом треугольник АВС содержит заданные окружности. Найдите геометрическое место центров окружностей, вписанных в треугольник АВС (при перемещении А).

9. На плоскости расположены два равнобедренных не пересекающихся прямоугольных треугольника ABC и DEC (AB и DE - гипотенузы, АВDЕ - выпуклый четырехугольник), причем AB = 2 DE . Построим еще два равнобедренных прямоугольных треугольника: BDF (с гипотенузой BF, расположенной вне треугольника BDC) и AEG (с гипотенузой AG, расположенной вне треугольника AEC). Докажите, что прямая FG проходит через точку N такую, что DCEN - квадрат.

10. Школьник написал домашнее сочинение на тему "Как я провел лето". Два его товарища из соседней школы решили не утруждать себя работой и переписали его сочинение. Но при переписывании они сделали несколько ошибок - каждый свои. Прежде чем сдать работы, оба школьника дали переписать сочинения четырем другим своим товарищам (каждый дал двум знакомым). Эти четыре школьника делают то же самое и т. д. При каждом переписывании сохраняются все предыдущие ошибки и, возможно, делаются новые. Известно, что в какой-то день в каждом новом сочинении оказалось не менее 10 ошибок. Докажите, что был такой день, когда в сумме было допущено не менее 11 новых ошибок.

Математика. 10 класс.

Примечание: в целях максимальной совместимости с различными программами просмотра html-страниц в условиях некоторых задач по математике радикалы n-й степени заменены на возведение в степень 1/n.

1. Назовем "соросовским произведением" двух различных чисел, a и b, число a + b + ab. Можно ли, исходя из чисел 1 и 4, после многократного применения этой операции к уже полученным произведениям получить:

а) число 1999; б) число 2000?

2. На валютной бирже продаются динары (D), гульдены (G), реалы (R) и талеры (T). Биржевые игроки имеют право совершать сделку купли-продажи с каждой парой валют не более одного раза в день. Курсы обмена следующие: D = 6G; D = 25R; D = 120T; G = 4R; G = 21T; R = 5T. Утром у игрока имелось 32 динара. Какое максимальное число

а) динаров; б) талеров он может получить к вечеру?

3. Центр окружности, проходящей через середины всех сторон треугольника АВС, лежит на биссектрисе его угла С. Найдите сторону АВ, если ВС = а, АС = b (a не равно b).

4. Решите уравнение

16x3 = (11x2 + x - 1)(x2 - x + 1)1/2 .

5. Известно, что существует прямая, делящая периметр и площадь некоторого описанного около окружности многоугольника в одном и том же отношении. Докажите, что эта прямая проходит через центр указанной окружности.

6. Пусть a3 - a - 1 = 0. Найдите точное значение выражения

(3a2-4a)1/3 + a(2a2+3a+2)1/4

Обратите внимание! В этой формуле была опечатка - последняя цифра во второй скобке была 3, а нужно 2.

7. Пусть прямая, перпендикулярная стороне AD параллелограмма ABCD, проходящая через точку В, пересекает прямую CD в точке M, а прямая, проходящая через точку В и перпендикулярная стороне CD, пересекает прямую AD в точке N. Докажите, что прямая, проходящая через точку В перпендикулярно диагонали АС, проходит через середину отрезка MN.

8. Имеется 100 положительных чисел a1, a2, ..., a100 таких, что

(a1+1)-1+(a2+1)-1+...+(a100+1)-1 < 1.

Докажите, что a1*a2*...*a100 > 99100.

9. Докажите, что для любого l > 3 найдется число х, для которого

sin x + sin (lx) > 1,8

10. Возьмем на стороне ВС треугольника АВС произвольную точку D и проведем окружность через точку D и центры окружностей, вписанных в треугольники ABD и АCD. Докажите, что все окружности, полученные для различных точек D стороны ВС, имеют общую точку

Математика. 11 класс.

1. В игре участвуют два игрока А и Б. Игрок А задаёт значение одного из коэффициентов a, b или c многочлена

x3 + ax2 + bx + c.

Игрок Б указывает значение любого из двух оставшихся коэффициентов. Затем игрок А задаёт значение последнего коэффициента. Существует ли стратегия игрока А такая, что как бы ни играл игрок Б, уравнение

x3 + ax2 + bx + c = 0

имеет три различных (действительных) решения?

2. Пусть

f(x) = (...((x - 2)2 - 2)2 - 2)2... - 2)2

(здесь скобок ( ) - n штук). Найдите f''(0)

3. Числа a , b и c таковы , что

a2 + b2 + c2 = 1.

Докажите, что a4 + b4 + c4 + 2(ab2 + bc2 + ca2)2 < 1. При каких a, b и c неравенство превращается в равенство?

4. Пусть прямая L перпендикулярна плоскости P. Три сферы попарно касаются друг друга так, что каждая сфера касается плоскости P и прямой L. Радиус большей сферы равен 1. Найдите минимальный радиус наименьшей сферы.

5. На валютной бирже острова Удача продают динары (D), гульдены (G), реалы (R) и талеры (T). Биржевые маклеры имеют право совершить сделку купли-продажи с любой парой валют не более одного раза за день. Курсы валют такие: D = 6G, D = 25R, D = 120 T, G = 4R, G = 21T, R = 5T. Например, запись D = 6G означает, что 1 динар можно купить за 6 гульденов (или 6 гульденов можно продать за 1 динар). Утром у маклера было 80 динаров, 100 гульденов, 100 реалов и 50400 талеров. Вечером у него было одинаковое число динаров и талеров. Каково максимальное значение этого числа?

6. Известно, что n-вершинник содержит внутри себя многогранник M с центром симметрии в некоторой точке Q и сам содержится в многограннике, гомотетичном M, с центром гомотетии в точке Q и коэффициентом k . Найдите наименьшее значение k, если

а) n = 4, b) n = 5.

7. Докажите, что существуют арифметические прогрессии произвольной длины, состоящие из различных попарно взаимно простых натуральных чисел.

8. Докажите, что плоскость, делящая в одинаковом отношении площадь поверхности и объем описанного многогранника, проходит через центр вписанной в этот многогранник сферы.

9. Найдите наибольшее c такое, что для любого l > 1 найдется a, удовлетворяющее неравенству

sin a + sin al > c.

10. В треугольнике ABC угол A равен a, а угол B равен 2a. Окружность с центром в точке C радиуса CA пересекает прямую, содержащую биссектрису внешнего угла при вершине B в точках M и N. Найдите углы треугольника MAN.

Физика

Физика. 10 класс.

1. С какой скоростью нужно бросить вертикально вверх камень, чтобы его перемещение за четвертую секунду составило ровно 1 метр?

2. Заяц бежит по прямой с постоянной скоростью 5 м/с. В некоторый момент его замечает лиса и начинает погоню. Скорость лисы меньше, чем у зайца, она постоянна по величине и составляет 4 м/с, движется лиса тоже не самым лучшим образом - скорость ее в каждый момент направлена точно в ту точку, где находится заяц. Вначале расстояние между ними уменьшается, затем начинает возрастать. Минимальное расстояние между лисой и зайцем составляет 30 м. Какое ускорение было у лисы в тот момент, когда расстояние было минимальным?

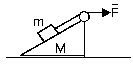
3. Тележка массы m находится на наклонной поверхности клина массы М (рис.1). К тележке привязана нить, переброшенная через блок, закрепленный на верхнем ребре клина. К свободному концу нити приложена горизонтальная сила F. При каком значении силы F клин и тележка могут двигаться вместе, без проскальзывания? Угол при основании клина a. Трения нет. Кусок нити между блоком и тележкой параллелен наклонной грани клина.


Рис. 1

4. На гладком горизонтальном столе происходит лобовой удар двух одинаковых тел: одно из них вначале покоится, другое налетает на него со скоростью v0. В каком направлении и с какой скоростью будет двигаться после удара налетевшее тело, если при ударе в тепло переходит 1% максимальной энергии деформации тел?

5. Высокий вертикальный сосуд содержит небольшое количество гелия под поршнем массы М, на который поставлена гиря массы 49 М. В состоянии равновесия поршень "висит" над дном сосуда на высоте h. Гирю снимают с поршня, и он начинает движение вверх. Оцените максимальную высоту подъема поршня. На какой высоте над дном сосуда поршень в конце концов остановится? Считайте при расчете, что трения в системе нет, стенки и поршень совершенно не проводят тепло, а теплоемкость стенок и поршня сосуда очень мала. Опыт проводят на Луне, где сила тяжести в шесть раз меньше, чем на Земле. Атмосферы на Луне нет.

6. Внутри большого теплоизолированного сосуда находится 32 г кислорода, температура сосуда и кислорода 300 К, манометр показывает давление 1 атм. Еще внутри сосуда находится очень легкая, маленькая капсула, содержащая 1 г гелия при температуре 500 К. Капсула лопается, и гелий выходит из нее в сосуд. Как будут меняться со временем показания манометра? Теплоемкость большого сосуда составляет 1000 Дж/К.

7. Для того чтобы не пришлось запоминать значение числа p ( p = 3,1415926...) электротехник решил соединить несколько резисторов и получить сопротивление, равное примерно p Ом ( а омметр у него всегда с собой ). В его распоряжении пять резисторов, их сопротивления равны, соответственно, 1, 2, 3, 4 и 5 Ом. Как их нужно соединить между собой для получения по возможности точного числа? Какая при этом получится точность?

8. К батарейке U = 1,5 В подключена очень длинная цепь из множества одинаковых амперметров и такого же количества одинаковых вольтметров (рис. 2). Каждый из амперметров имеет сопротивление r = 1 Ом, сопротивление каждого вольтметра R = 10 кОм. Что показывают первый и второй амперметры? Найдите сумму показаний всех амперметров и сумму показаний всех вольтметров в этой цепи


Рис. 2

Физика. 11 класс.

1. Заяц бежит по прямой с постоянной скоростью 5 м/с. В некоторый момент его замечает лиса и начинает погоню. Скорость лисы меньше, чем у зайца, она постоянна по величине и составляет 4 м/с, движется лиса тоже не самым лучшим образом - скорость ее в каждый момент направлена точно в ту точку, где находится заяц. Вначале расстояние между ними уменьшается, затем начинает возрастать. Минимальное расстояние между лисой и зайцем составляет 30 м. Какое ускорение было у лисы в тот момент, когда расстояние было минимальным? Оцените ускорение лисы за одну секунду до этого момента.

2. На горизонтальной поверхности стола находится большой и очень легкий куб (рис. 3). На его верхней гладкой грани помещен кубик массы М, к которому при помощи легких нерастяжимых нитей привязаны кубики М и 2М. Нити переброшены через блоки, закрепленные на противоположных ребрах верхней грани, свисающие концы нитей вертикальны. Систему растормаживают. При каком значении коэффициента трения между большим кубом и столом этот куб может оставаться неподвижным?


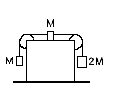
Рис. 3

3. На гладком горизонтальном столе происходит лобовой удар двух одинаковых тел: одно из них вначале покоится, другое налетает на него со скоростью Vo. Оцените скорость, с которой будет двигаться после удара налетевшее тело, если в тепло переходит 90% максимальной энергии деформации тел при таком ударе.

4. Конденсаторы С, 2С и 3С соединены между собой, как показано на рисунке 4. Между свободными выводами конденсаторов С и 2С подключен резистор 3R, между свободными выводами конденсаторов С и 3С - резистор 2R, между оставшимися - резистор R. В начальный момент конденсатор 2С заряжен до напряжения U, остальные конденсаторы не заряжены. Какое количество тепла выделится за большое время на резисторе R? На резисторе 2R? На резисторе 3R?


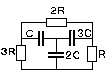
Рис. 4

5. Две одинаковые катушки индуктивности расположены недалеко друг от друга. Одна из них подключена к источнику синусоидального переменного напряжения последовательно с амперметром, к концам другой катушки подключен второй амперметр. Амперметры показывают 1 А и 0,2 А (угадайте сами, какой из них показывает 1 А, а какой - 0,2А). Один из амперметров отключают (при отключении амперметра цепь разрывается). Что покажет после этого оставшийся амперметр? Катушки, приборы и источник можно считать идеальными. Сопротивление проводов пренебрежимо мало.

6. К источнику переменного напряжения, частоту которого можно изменять в широких пределах, подключена цепь из двух одинаковых катушек L, двух конденсаторов С и амперметра переменного тока с очень малым сопротивлением (рис. 5). Амплитуда напряжения источника U0. На какой частоте сила тока через амперметр будет минимальна? Чему равна амплитуда этого тока? Элементы цепи считайте идеальными.


Рис. 5

7. В большом спортивном зале стены, пол и потолок оклеены звукопоглощающими (полностью поглощающими звук) покрытиями. На высоте h = 5 см от пола находится мощный точечный источник звука частоты f = 2000 Гц, излучающий звуковые волны равномерно во все стороны. Микрофон малых размеров находится на высоте Н = 3 м от пола на расстоянии L = 4 м по горизонтали от источника. Подключенный к микрофону чувствительный вольтметр показывает амплитуду переменного напряжения U = 0,01 В. Как изменятся показания этого вольтметра, если удалить звукопоглощающее покрытие на полу под микрофоном? Считайте, что от пола звуковые волны отражаются без потерь энергии. Какими будут показания вольтметра в том случае, когда покрытие на полу будет восстановлено (но оно окажется очень тонким, качеством похуже и будет поглощать только половину падающей энергии волны, а ослабленная волна будет отражаться от пола зеркально)?

8. На расстоянии d = 0,6 см от центра стеклянного шара радиуса R = 1 см находится точечный источник света. При каких значениях коэффициента преломления стекла n весь испускаемый источником световой поток выйдет наружу? Оценить долю вышедшего наружу потока при значении n1=1,7. Снаружи - вакуум, источник излучает во все стороны равномерно.

Химия

Химия. 9 класс.

1. Во время ремонта в лаборатории случайно покрасили одинаковой краской баллоны с водородом и метаном. Предложите три разных способа определения: в каком баллоне какой газ находится. Приведите, если нужно, уравнения реакций.

2. Мама поручила юному химику "посмотреть за кашей". Вместо того чтобы помешивать варящуюся кашу, он просто смотрел на эмалированную кастрюлю. В результате каша подгорела. Чтобы отмыть кастрюлю, юный химик залил ее 40%-м раствором гидроксида натрия и подогрел. Нагар растворился, эмаль - тоже.
1. Почему без перемешивания каша подгорает?
2. Почему растворилась эмаль? Приведите возможные уравнения реакций.
3. Какие правила техники безопасности нарушил юный химик?

3. Автор средневекового алхимического трактата приводит следующий рецепт "водки для золота":

"Возьми совершенно сухого венгерского синего купороса и селитры, более фунта нашатырной соли. Сделай из этого крепкую водку в стеклянном, хорошо замазанном сосуде, снабженном стеклянной крышкой или колпаком".
1. Какие реактивы предлагает использовать алхимик? Приведите их формулы.
2. Как "сделать водку" из этих реактивов? Опишите последовательность операций, укажите условия проведения реакций.
3. Приведите уравнения реакций. Какой качественный состав имеет "водка для золота"?
4. Напишите уравнение реакции растворения золота в этой "водке".

4. В два стеклянных сосуда, соединенных с манометрами для измерения давления, поместили пучки медной проволоки, распределенные по всему объему сосудов. Затем первый сосуд наполовину заполнили 15%-й соляной кислотой. Оставшийся объем сосуда заполнили кислородом до давления 1 атм. Второй сосуд наполовину заполнили 37%-й соляной кислотой. Оставшийся объем второго сосуда заполнили аргоном до давления 1 атм. Оба сосуда изредка покачивали для перемешивания. Через некоторое время оказалось, что давление в обоих сосудах изменилось, причем в одном из них оно уменьшилось, а в другом увеличилось.
1. Какие реакции могли протекать в первом и втором сосудах? Приведите уравнения.
2. В каком сосуде давление уменьшилось и почему?
3. В каком сосуде давление увеличилось и почему?
4. Известно, что согласно положению в ряду напряжений (активности) металлов медь не реагирует с соляной кислотой. Почему в описанных случаях возможно протекание реакций?

5. Лаборант решил обезвредить ртуть из разбитого термометра. Для этого он залил собранную ртуть смесью крепкой соляной кислоты с небольшим количеством азотной кислоты и оставил в закрытой банке на несколько суток. Получившийся белый осадок лаборант растворил в избытке азотной кислоты. Все работы лаборант выполнял на алюминиевом поддоне. Случайно пролитый на поддон сильнокислый раствор лаборант тщательно нейтрализовал содой и вытер. В результате неаккуратной работы у лаборанта сильно корродировали алюминиевый поддон и вилка, которой он пользовался в столовой.
1. Напишите уравнения упомянутых реакций.
2. Какие ошибки допустил лаборант?
3. Ваш младший брат (сестра) разбил медицинский термометр, взрослые придут не скоро. Что вы будете делать?

6. В колбе объемом 2,8 л содержится 7,0 г индивидуального газа при 0 oC и 2 атм.
1. Какой это может быть газ? Приведите не менее трех вариантов ответа.
2. Для каждого варианта напишите уравнение реакции этого газа с кислородом.

7. В качестве консервирующей добавки при производстве газированных (шипучих) вин используется оксид серы (IV) (сернистый ангидрид) в количестве до 400 мг на литр вина. Растворимость оксида углерода (IV) в газированных напитках - около 800 мл газа на литр жидкости при комнатной температуре (20 oС).
1. Сколько процентов (по объему) сернистого ангидрида содержит углекислый газ, используемый для производства шипучих вин?
2. Как обнаружить примесь сернистого ангидрида в углекислом газе? Приведите уравнения реакций.

8. Лаборант случайно разбил склянку с реактивом. На полу среди бесцветных кристаллов лежал кусок этикетки с надписью: "...стый перегнанный". Догадавшись, что было в банке (соль, не содержащая редких или ядовитых элементов), лаборант стал убирать с пола остатки мокрой тряпкой... Произошел довольно громкий хлопок, комната наполнилась клубами очень едкого тумана. Удивленный лаборант (к счастью, он работал в маске) решил проанализировать оставшиеся кристаллы. Навеску массой 0,445 г он осторожно растворил в 100 мл 5%-й азотной кислоты и добавил избыток раствора нитрата серебра. Выпал белый творожистый осадок, масса которого после высушивания составила 1,435 г. Результаты анализа соответствовали первоначальной догадке лаборанта.
1. Какой состав имела соль из разбитой банки?
2. Почему эта соль бурно реагировала с мокрой тряпкой?
3. Почему лаборант растворял соль не в воде, а в разбавленной азотной кислоте?
4. Почему эту соль можно очищать перегонкой? В каких условиях это делают?
5. Можно ли убирать данный реактив мокрой тряпкой, если на этикетке написано "кристаллический"? Чем отличается "кристаллический" реактив от "перегнанного"?

9. Напишите формулы и названия всех известных вам кислот, образованных хлором, водородом и кислородом.
1. Для каких из перечисленных кислот хлора существуют аналогичные кислоты фтора? Напишите их формулы и названия.
2. Какие степени окисления проявляют фтор и хлор в этих кислотах? Сколько связей они при этом образуют? Объясните на основании электронного строения атома, почему не для всех кислот хлора есть аналогичные кислоты фтора.

10. В каких случаях при разложении безводных солей образуются свободные металлы? Приведите не менее трех разных примеров, напишите уравнения реакций.

Химия. 10 класс.

1. Одним из недавно разработанных методов гидрирования углеводородов является обработка непредельного соединения литием и гексагидратом хлорида никеля. Напишите уравнения возможных реакций, протекающих при гидрировании гексена-1, и объясните роль каждого из компонентов смеси в процессе гидрирования.

2. При изготовлении "золотой" и "серебряной" красок используют порошкообразные металлы или их сплавы. Напишите уравнения реакций, с помощью которых можно установить, что является основным компонентом а) "серебряного" порошка, б) "золотого" порошка:
а) серебро, алюминий или "новое серебро" (нейзильбер);
б) золото, бронза или латунь.
(В ответе укажите на характерные признаки протекающих реакций, наблюдая которые вы будете устанавливать состав порошков: появление осадка и его цвет, изменение окраски раствора, выделение газа и т. д.)

3. При сливании 50 мл раствора соли А и 50 мл раствора соли Б выпало 2,69 г осадка, содержащего, по данным элементного анализа, 1,5% водорода, 14,9% кальция, 23,8% серы, 24,2% цинка и кислород. При упаривании фильтрата получают менее 0,01 г сухого остатка.
1. Установите формулы солей.
2. Напишите уравнение проведенной реакции.
3. Вычислите содержание солей в исходных растворах в г/л.

4. Жидкость А получена упариванием при 150-200 oС водного раствора соединения Х, которое широко используется в технике. При полном сгорании образца А массой 2,84 г в атмосфере кислорода образовались только диоксид углерода массой 3,52 г и вода - 2,52 г.
1. Установите молекулярную формулу вещества Х и количественный состав жидкости А.
2. Предложите возможные структурные формулы вещества Х и выберите из них наиболее вероятную, отвечающую условию задачи.
3. Как называют выбранное вами соединение Х в технике и в справочной литературе? Какое практическое применение оно находит?

5. Продукты полного сгорания 0,512 г смеси бензола, стирола и циклогексана в избытке кислорода были пропущены последовательно через трубку с сульфатом меди и сосуд, содержащий 17,5 мл 16,25%-го раствора едкого кали (плотность раствора равна 1,142 г/мл). Масса трубки при этом возросла на 0,504 г.
1. Напишите уравнения проведенных реакций.
2. Вычислите массовые доли соединений, содержащихся в растворе после окончания поглощения продуктов сгорания.

6. При медленном растворении 10,0 г смеси мелкоизмельченного металлического железа с его оксидами (II и III) в избытке 10%-й соляной кислоты (плотность равна 1,05 г/мл) выделяется 604 мл газа, измеренного при 20 oС и давлении 756 мм рт. ст.
1. Напишите уравнения химических реакций, протекающих при растворении смеси.
2. Вычислите минимальное и максимальное содержание каждого из компонентов смеси (в процентах по массе).
3. Вычислите возможные минимальный и максимальный объемы кислоты, необходимые для растворения смеси.

7. Избыток газообразного бромоводорода пропускают в раствор стирола в толуоле в присутствии органического пероксида. Напишите уравнения всех протекающих реакций.

8. При взаимодействии предельных углеводородов с хлором образуются смеси хлорпроизводных сложного состава. Разделение этих смесей, содержащих в том числе и изомерные вещества с весьма близкими физическими свойствами, в лабораторных условиях представляет собой очень трудную экспериментальную задачу и часто просто невыполнимо. Поэтому для получения индивидуальных соединений обычно используют синтетические методы, позволяющие получать каждое из веществ с высоким выходом.
1. Сколько может существовать хлорэтанов состава C2H6-xClx? Напишите их структурные формулы.
2. Предложите схемы синтеза каждого из этих соединений, исходя из этанола. Укажите в схемах необходимые реагенты и условия проведения реакций.

9. Для получения различных карбениевых ионов R1R2R3C+ используют либо реакции присоединения протона или других электрофильных агентов к двойной связи С=С (С=Х), либо реакции гетеролитического разрыва связи R1R2R3C-Х. При этом ионизация идет тем легче, чем стабильнее уходящая группа Х, поэтому в случае малоустойчивых карбокатионов ионизацию инициируют действием солей серебра (отщепляется галогенид серебра) или сильных кислот Льюиса типа SbF5 (отщепляется устойчивый анион типа SbF6-). Аналогичные реакции с образованием алкенильных катионов R1R2C=С(R3)+ также описаны, но реализовать их гораздо труднее из-за меньшей устойчивости винильных катионов. Все попытки получить ацетиленовый катион RC=C+ реакцией ионизации были безуспешными из-за еще большей нестабильности катионов такого типа (очевидно, реакция присоединения электрофилов к кратной связи здесь в принципе невозможна). Не подходят для этого и диазониевые катионы типа RC=CN2+, поскольку они очень устойчивы и не теряют молекулы азота даже при нагревании. Тем не менее ацетиленовые катионы все же были генерированы (хотя и в очень малом количестве), и изучены их реакции с различными реагентами. Предложите возможный способ получения таких катионов.

10. Один из гальванических элементов представляет собой стеклянный сосуд, в который погружен керамический сосуд из обожженной пористой глины. В оба сосуда помещают разбавленные растворы серной кислоты: в стеклянный - 5%-й раствор, в керамический - 10%-й раствор. Если теперь в сосуды поместить пластины из платинированного угля и замкнуть цепь, то в цепи появляется электрический ток.
1. Напишите уравнения реакций, протекающих при работе этого элемента.
2. Поясните принцип действия гальванического элемента, подтвердив его расчетом.
3. В каком из растворов находится отрицательный полюс элемента?
4. Будет ли работать этот элемент при замене раствора серной кислоты на: а) соляную кислоту; б) раствор щелочи; в) раствор хлорида натрия? Ответ поясните.

Химия. 11 класс.

1. Для полного сгорания 20 мл вещества А и такого же количества вещества Б потребовалось одинаковое количество кислорода. Продукты сгорания А были полностью поглощены щелочью, а после обработки избытком щелочи продуктов сгорания Б было получено 20 мл газа В, не поддерживающего горения. Определите возможные структуры А и Б.

2. Два индивидуальных вещества A и Б (жидкости при обычных условиях) реагируют между собой в присутствии каталитических количеств воды с образованием кристаллической соли В, которая при нагревании разлагается на два простых вещества.
1. Что представляют собой вещества А-В? Предложите два варианта решения.
2. Напишите уравнения реакций.

3. В одном из решений задач Соросовской олимпиады было приведено уравнение реакции: NaOH + Ne = NeOH + Na. Это уравнение содержит две грубые ошибки: гидроксид неона не существует, а неон не вступает в реакцию замещения с NaOH. Тем не менее известно, что неон способен реагировать с некоторыми веществами в определенных условиях.
1. Какие соединения гелия, неона и аргона вы знаете (или предполагаете их существование)?
2. Как их можно получить? Напишите уравнения реакций.

4. Выдающийся датский физик Нильс Бор в 1943 г. был вынужден бежать в Англию из оккупированного немцами Копенгагена, чтобы избежать ареста. Его тайно вывезли на бомбардировщике, в бомбовом отсеке. Бору пришлось оставить все ценные вещи дома, однако он успел кое-что предпринять для их сохранности. Так, он растворил одну из своих научных наград - золотую медаль имени Макса Планка - в специальной жидкости и оставил раствор на полке. Вернувшись домой после войны, он выделил золото из этого раствора, и ему снова отчеканили медаль.
1. Назовите четыре реактива, которые можно использовать для растворения золота, и напишите уравнения соответствующих реакций. Какой из этих реактивов, по-вашему, использовал Бор?
2. Предложите способ регенерации золота из раствора, полученного Бором.

5. Один американский профессор решил проверить своих коллег на умение уравнивать окислительно-восстановительные реакции и предложил им "химического монстра": уравнение реакции окисления комплекса [Cr(CO(NH2)2)6]4[Cr(CN)6]3 сернокислым раствором перманганата калия. Через некоторое время американцу ответил израильский профессор, который сообщил, что ничего необычного в этом уравнении нет: он нашел коэффициенты во время занятий со студентами меньше чем за 20 минут (при этом успевая отвечать на вопросы студентов).
1. Определите степени окисления элементов в комплексе-восстановителе.
2. Определите продукты этой реакции, если известно, что все элементы-восстановители окисляются до высшей возможной степени окисления.
3. Найдите коэффициенты в уравнении реакции методами а) электронного, б) электронно-ионного баланса. (Подсказка: сумма коэффициентов в правой части уравнения больше 4000.) В обоих случаях засеките время и сообщите свой результат.

6. pH 0,163%-го водного раствора одноосновной кислоты равен 2,609. При разбавлении раствора в два раза pH увеличивается до 2,766.
1. Определите константу диссоциации кислоты.
2. Рассчитайте молярную концентрацию кислоты в исходном растворе.
3. Найдите молярную массу и формулу кислоты, если плотность исходного раствора равна 1,000 г/мл.
4. Насколько может увеличиться pH раствора любой одноосновной кислоты при разбавлении в n раз? Определите минимальное и максимальное значения DpH.
Диссоциацией воды при решении задачи можно пренебречь.

7. В начале 1960-х гг. проходили переговоры о запрещении ядерных испытаний в атмосфере. Во время переговоров один из экспертов заявил, что на полигоне в пустыне Невада (США) радиоактивные изотопы распадаются быстрее, чем на Новой Земле (СССР) из-за того, что в пустыне более высокая температура. Советский эксперт возразил, что периоды полураспада радиоактивных веществ не зависят от температуры. Кто из экспертов был прав? Зависят ли периоды полураспада от температуры? Кратко объясните вашу точку зрения.

8. При действии радиоактивного излучения на смесь паров четыреххлористого углерода с этиленом была получена жидкость Х, содержащая 37,6% хлора по массе. Обработка жидкости Х избытком раствора аммиака при нагревании приводит к образованию соединения Y, содержащего 4,91% азота по массе. Вещество Y может быть использовано для изготовления мыла и шампуней, "от которых дети не плачут", а длительное нагревание Y при 300-350 oС приводит к повышению содержания азота до 5,24% и образованию расплава вещества Z, который может быть использован для промышленного получения синтетического волокна.
1. Установите молекулярные формулы соединений X, Y и Z.
2. Предложите структурные формулы этих веществ и напишите уравнения проведенных реакций.
3. Объясните, почему соединение Y обладает моющим (детергентным) действием и почему от мыла, изготовленного на его основе, дети не плачут.
4. Предложите возможную схему механизма образования соединений Х и Y.

9. Вещество А после обработки хлористым тионилом реагирует с изомерным веществом Б, присутствующим в продуктах гидролиза большинства природных пептидов. Гидрогенолиз продукта этой реакции (т. е. разложение при действии водорода) приводит к веществу В, также входящему в состав пептидных гидролизатов. Полный гидролиз В дает продукты Г и Б, массовая доля азота в которых отличается в 2,20 раза.
1. Нарисуйте структурные формулы веществ А, Б, В и Г.
2. Напишите уравнения реакций, упомянутых в задаче.
3. Сколько нециклических соединений, относящихся к тому же классу, что и В, можно построить из одной молекулы Б и двух молекул Г, не затрагивая связи C-C и N-N?
4. Нарисуйте структурную формулу вещества, изомерного Б, которое при гидролизе образует соединение В. Имеет ли это вещество изоэлектрическую точку?

10. Молекула фуллерена C60 представляет собой геометрическую фигуру, называемую икосаэдром. В каждой вершине икосаэдра находится атом углерода, связанный с тремя другими атомами с помощью s-связей:

Для описания p-электронных состояний этой молекулы используют модель свободных электронов, движущихся по сфере радиуса r. В рамках этой модели уровни энергии описываются выражением:

EL=(h2/(2mr2))L(L+1)

где h=1,05*10-34 Дж*с - постоянная Планка; m=9,11*10-31 кг - масса электрона; L - орбитальное квантовое число (L = 0, 1, 2...). Для каждого L существуют (2L + 1) уровней с одинаковой энергией.
1. Сколько p-электронов имеет молекула C60 ?
2. Какое значение квантового числа L имеет высший заполненный уровень в основном состоянии C60?
3. Сколько неспаренных электронов должна иметь молекула C60 в соответствии с этой моделью?
4. Рассчитайте радиус молекулы C60, если известно, что разница в энергии между двумя высшими заполненными уровнями составляет 296 кДж/моль.
5. Известно, что в основном состоянии C60 не имеет неспаренных электронов. Для того чтобы объяснить этот факт, необходимо учесть, что форма молекулы не сфера, а икосаэдр. В икосаэдре уровни энергии с квантовым числом L > 2 расщепляются на группы, содержащие 1, 3, 4 или 5 уровней с одинаковой энергией. На какие группы расщепляется уровень с L = 5, если известно, что при этом не образуется одиночных уровней?
6. С учетом расщепления определите число неспаренных электронов в основном состоянии молекул K3C60 и K6C60.

Биология

Дорогие друзья!

Первый тур нашей олимпиады отличается от последующих тем, что он является заочным: время для подготовки и написания ответов не ограничивается несколькими часами, к тому же можно использовать любую литературу. В этом году вариант заочного тура состоит из двух частей: задачи 1-3 рассчитаны прежде всего на работу с литературой, а задачи 4-7 построены так же, как и задачи очных туров (их можно считать тренировочными).

Учащихся, приступающих к решению наших задач, хотелось бы предостеречь от одного типичного заблуждения. Возможность обращаться к литературе при подготовке ответов вовсе не означает, что олимпиадные работы должны напоминать рефераты, а состязание сведется к выяснению того, кто из школьников проявил больше усидчивости и работал в более богатой библиотеке.

Осмысление уже известных фактов - важная часть биологического исследования. Научные проблемы не возникают в готовом виде: "Исходя из перечисленных известных фактов, определить то-то и то-то". Для ученого крайне важно умение собирать необходимую информацию и анализировать ее, проверять разные версии, сопоставляя вытекающие из них выводы с уже установленными свойствами живых организмов. Вот почему на заочном туре вам предложены задачи, для решения которых понадобится согласовывать "полет фантазии" при создании собственных гипотез и анализ фактического материала, найденного в литературе (учебниках, справочниках, энциклопедиях, научно-популярных книгах и др.).

Задачи 1-3 в варианте каждого класса состоят из двух частей - пунктов а) и б). В пункте а) требуется ответить на конкретный вопрос о свойствах нескольких организмов, органов или других биологических объектов. После этого в пункте б) нужно сделать выводы: обобщить данные, выдвинуть новые версии и т. п. Мы старались, чтобы решение задач продвинуло вас в понимании ряда важных биологических понятий. Знакомство с ними ценно не только и не столько для успеха на олимпиаде (вовсе не обязательно в задачах второго тура встретятся те же самые понятия), но прежде всего - для расширения ваших знаний. В связи с этим не стоит переживать, если для некоторых объектов, упомянутых в пункте а), вам не удастся найти требуемые сведения. Обычно можно перейти к пункту б) и хорошо с ним справиться, даже не до конца разобрав пункт а).

Внимание! На вторую страницу работы выносятся ответы только на пункт а) и только для задач 1 - 3 ! При этом достаточно вместо названий организмов, органов или процессов написать их номера в перечне. В ряде случаев названия организмов, приведенные в условиях задач, объединяют несколько биологических видов. Если ответ на поставленный вопрос для разных видов неодинаков, вам следует это указать.

В решении задачи, прежде чем приступать к анализу пункта б, нужно повторить ответ на пункт а), т. е. текст, вынесенный на вторую страницу работы.

Стремитесь к лаконичности изложения! Переписывание в тетрадь сведений, которые как-то характеризуют рассматриваемый биологический объект, но не помогают получить ответ на конкретно поставленный вопрос, не принесет вам никаких дополнительных баллов.

Желаем успехов!

Биология. 9 класс.

1. Известный эколог Л. Г. Раменский разделил живые организмы на три группы по стратегиям выживания в природных сообществах (экосистемах): виоленты (образно названные им "львами"), патиенты ("верблюды") и эксплеренты ("шакалы"). "Львы" - сильные конкуренты, захватывающие весь широкий диапазон условий, в котором могут жить. "Верблюды" обитают лишь в условиях с бедными ресурсами и переносят тяготы жизни благодаря наличию специальных приспособлений. "Шакалы", как и "львы", предпочитают изобилие ресурсов, но, в отличие от них, являются слабыми конкурентами: всплески численности "шакалов" происходят в периоды временного отсутствия "львов".

а) К каким из описанных выше групп относятся следующие растения: 1) дуб, 2) ива, 3) ковыль, 4) копытень, 5) лиственница, 6) малина, 7) орляк, 8) пырей, 9) рис, 10) саксаул?

б) Объясните, почему разделение на "львов", "верблюдов" и "шакалов" является условным. В каких случаях живые организмы занимают промежуточное положение между этими группами или могут быть отнесены сразу к нескольким из них? Приведенные вами соображения подтвердите примерами.

2.

а) Какие из перечисленных ниже птиц выращиваются человеком с целью получения яиц: 1) гагара, 2) голубь, 3) гусь, 4) журавль, 5) индейка, 6) курица, 7) перепел, 8) страус, 9) утка, 10) цесарка?

б) Какими особенностями должна обладать птица, чтобы ее можно было использовать для выведения яйценосной породы? Для каждой из упомянутых вами особенностей приведите по 1-2 примера птиц (не упомянутых в пункте а), обладающих и не обладающих этой особенностью.

3. В трагедии В. Шекспира "Гамлет" Офелия, собрав букет цветов, раздает их придворным и членам королевской семьи как средства от разных болезней.

а) Сможет ли использовать в лечебных целях свой подарок придворный, получивший от Офелии: 1) алтей, 2) валериану, 3) крапиву, 4) лопух, 5) мать-и-мачеху, 6) мяту, 7) ноготки, 8) одуванчик, 9) полынь, 10) пырей, 11) шалфей, 12) щавель конский?

б) Обоснуйте ответы, данные вами в пункта а). Конечно, Офелию вряд ли можно считать идеальным фитотерапевтом. Чтобы лекарственные растения оказывали максимальный эффект, при их сборе следует учитывать много разных соображений. Какие советы вы могли бы дать сборщику лекарственных растений? Объясните, в чем состоит их целесообразность.

4. Весьма популярными мелиоративными мероприятиями являются осушение чрезмерно увлажненных почв и орошение тех участков, на которых наблюдается недостаток воды. Однако эти, казалось бы, полезные действия могут вызывать неблагоприятные последствия. Какие?

5. Многие болезни человека (как, впрочем, и болезни животных и растений) <тяготеют> к определенным сезонам: для одних пик заболеваемости приходится на лето, для других - на зиму и т. д. Перечислите причины, с которыми это может быть связано. Каждую из указанных вами причин проиллюстрируйте примерами.

6. Известно, что у некоторых видов термитов и муравьев существуют солдаты-"камикадзе". Эти особи, вступая в сражение с врагами, жертвуют собой: при сильном сокращении мускулатуры брюшко разрывается, и содержащаяся в нем ядовитая жидкость обрушивается на неприятеля. Это свойство, безусловно, полезно для термитника (муравейника) в целом, но лишь при ограниченном его использовании (не всеми солдатами и не при любой угрозе) - ведь иначе солдат вообще не останется. Как же в муравейнике (термитнике) может регулироваться интенсивность применения данного способа защиты и нападения? Предложите ваши гипотезы и опишите способы их проверки.

7. Из записных книжек Кифы Мокиевича: "Ученые патетически описывают, что разные водные организмы могут накапливать определенные ионы в крайне высоких концентрациях. Например, в теле асцидий содержание ванадия - редчайшего элемента - достигает 0,16%. А вспомним огромные залежи железа и марганца на дне Мирового океана, созданные микроорганизмами! Восхитительно? На самом деле надо не восторгаться, а спасать природу. Ценные соединения захватываются немногими счастливчиками и надолго выводятся из круговорота веществ. Снижение численности этих "Плюшкиных" до минимального уровня позволит повысить продуктивность экосистем!"
Что вы могли бы возразить Кифе Мокиевичу?

Биология. 10 класс.

1. Физиологи выделяют две группы желез внутренней секреции - зависимые и независимые от функций гипофиза.

а) К какой из этих групп следует отнести: 1) корковое вещество надпочечников, 2) мозговое вещество надпочечников, 3) поджелудочную железу, 4) половые жезезы, 5) околощитовидные железы, 6) щитовидную железу?

б) С помощью каких соединений гипофиз влияет на работу других желез внутренней секреции? В чем заключается это влияние? (В задаче рассматривается эндокринная система человека.)

2.

а) Свойственна ли перечисленным ниже животным: I) моногамия - образование при размножении пар между одним самцом и одной самкой, II) полиандрия - спаривание одной самки с несколькими самцами, III) полигиния - спаривание одного самца с несколькими самками: 1) антилопа, 2) горилла, 3) дрофа, 4) заяц, 5) курица, 6) лебедь, 7) лосось, 8) лось, 9) медоносная пчела, 10) морж, 11) слон, 12) удильщик, 13) тетерев, 14) шалашник, 15) якана?

б) Какие особенности образа жизни и строения животного позволяют с высокой вероятностью предположить, что данному виду свойственна моногамия; полиандрия; полигиния? Ответ аргументируйте, пояснив связи между этими особенностями и типом развития потомков.

3.

а) Какие из перечисленных ниже факторов вызывают уменьшение содержания белка в крови человека по сравнению с нормой: 1) воспаление желудочно-кишечного тракта, 2) гемофилия, 3) гепатит, 4) голодание, 5) задержка мочевыделения, 6) лактация, 7) повышение температуры тела, 8) сахарный диабет, 9) усиленное потоотделение, 10) цирроз печени?

б) Перечислите причины, которые могут приводить к изменению содержания в крови различных соединений. Какие вы можете предложить лечебные мероприятия, направленные на восстановление уровня этих соединений?

4. Можно выделить две основные стратегии хозяйственного использования человеком лесов. Первая стратегия состоит в последовательной сплошной вырубке отдельных участков леса, после чего на освободившихся пространствах растут новые деревья до тех пор, пока не приобретут "товарный вид". Вторая стратегия предполагает постоянную выборочную вырубку на всей территории леса. Оба варианта предусматривают использование и других лесных богатств - грибов, ягод и т. д. В чем вы видите преимущества и недостатки каждого из этих подходов?

5. При каких болезнях объявляют карантин, а при каких - нет? Чем это обусловлено? От чего зависит продолжительность карантина?
(В ответе постарайтесть не приводить длинные перечни болезней, а указать общие свойства, характерные для разных заболеваний.)

6. Халаддин, герой фантастического романа К. Ю. Еськова "Последний кольценосец", прославился тем, что доказал химическую природу межклеточных переносчиков нервного возбуждения, на несколько веков опередив современную ему науку. А как бы вы справились с этой задачей, а также с доказательством электрической передачи возбуждения по нервным клеткам: а) в наши дни; б) если бы дело происходило 100 лет назад? Опишите, какие эксперименты вы поставите, какие результаты предполагаете получить и как будете строить доказательство на основании этих результатов.

7. Д-ру Наплевайту поручили выяснить, существует ли у людей наследственная предрасположенность к некоторому заболеванию - синдрому наплевизма. Было установлено, что если родители страдают этой болезнью, то у их детей вероятность заболевания достоверно выше, чем в среднем в популяции. "Следовательно, - решил д-р Наплевайт, - предрасположенность к синдрому наплевизма передается по наследству". Однако д-ра Аккурата это доказательство не удовлетворило. По его мнению, существуют и другие причины, которые могут вызвать наблюдавшуюся д-ром Наплевайтом ситуацию.

Какие это могут быть причины? Для каких реальных болезней, по вашему мнению, эти причины могут проявиться так, как описано в задаче?

Опишите, как можно корректно доказать влияние наследственности на шанс заболеть той или иной болезнью. Для каких известных вам болезней существует наследственная предрасположенность, повышающая вероятность заболевания?

(Болезни, обязательно проявляющиеся у обладателей определенных наборов наследственных признаков, мы в этой задаче не рассматриваем.)

Биология. 11 класс.

1.

а) Какие из перечисленных ниже органов осуществляют функцию кроветворения (гемопоэза) в человеческом организме: 1) желтый костный мозг, 2) красный костный мозг, 3) лимфатические узлы, 4) миокард, 5) мозговой слой надпочечников, 6) печень, 7) подкожная клетчатка, 8) почки, 9) селезенка, 10) тимус?

б) Укажите какие именно форменные элементы крови образуются в различных органах кроветворения. Понятие "гемопоэз" не включает в себя образование различных химических соединений, входящих в состав крови. А если все-таки рассматривать процесс кроветворения в широком смысле, то какие органы войдут в ваш список? (При ответе на вопрос не ограничивайтесь перечнем из пункта а).) Объясните, какие именно вещества образуются в этих органах.

2. Часть белков в клетке синтезируется на рибосомах эндоплазматического ретикулума, а часть - на свободных рибосомах цитоплазмы. Как выяснилось, ретикулум - место сборки белков самого ретикулума, аппарата Гольджи, лизосом, а также секреторных белков и белков наружной мембраны. В цитоплазме же синтезируются белки цитоплазмы и ядра, а также митохондрий и хлоропластов, закодированные в ядерном геноме.

а) На каких рибосомах синтезируются: 1) актин, 2) антитела, 3) гистоны, 4) гликогенсинтетаза, 5) глобин, 6) гормон роста, 7) ДНК-полимераза, 8) казеин, 9) лактатдегидрогеназа, 10) пепсиноген, 11) рецептор инсулина, 12) фибриноген?

б) Обоснуйте ответы, данные вами в пункте а). Приведите еще по 3 примера белков, синтезируемых на ретикулуме и в цитоплазме.

3.

а) Для каких из перечисленных ниже комнатных растений родиной являются тропические леса: 1) алоэ, 2) венерин башмачок, 3) каланхое, 4) калла, 5) монстера, 6) опунция, 7) пассифлора, 8) традесканция, 9) филлодендрон, 10) <щучий хвост>?

б) Далеко не всякое тропическое и субтропическое растение можно сделать комнатным (т.е. добиться, чтобы оно успешно выращивалось в домашних условиях). Перечислите, с какими причинами может быть связана сложность или невозможность "приручения" таких растений.

4. В начале XVIII в. французский ученый Де Малье высказал мнение, что предками птиц были летучие рыбы. Какие факты, по вашему мнению, свидетельствуют против этой гипотезы? Ответ разделите на две части: I) сведения, известные современникам Де Малье, II) данные, которые были получены в более позднее время.

5. У различных видов животных органы чувств развиты по-разному: у одних видов - острое зрение, у других - острый слух и т.д. Как вы полагаете, какие особенности строения глаза, уха и т. д. характерны для организмов, наиболее чувствительных к соответствующим сигналам?

6. Различие четырех типов человеческого темперамента наглядно продемонстрировал датский карикатурист Х. Бидструп. На его рисунке изображено поведение в одной и той же ситуации холерика, флегматика, меланхолика и сангвиника (сверху вниз).

Можно ли рассматривать карикатуру Бидструпа как непосредственное руководство по определению темперамента людей? С какими причинами могут быть связаны ошибочные результаты подобного эксперимента?

Вам поручено выяснить, существуют ли эти четыре типа темперамента у морских свинок (или, если хотите, у каких-то других животных). Опишите, как вы будете решать эту задачу.

7. Д-р Паганель, прибыв на недавно открытый необитаемый остров, занимается описанием местной флоры и фауны и очень волнуется за судьбу тех видов живых организмов, которые нигде, кроме этого острова, не встречаются. "При последующем освоении острова, - рассуждает он, - жизнедеятельность человека может привести к истреблению этих видов. Поэтому надо начинать готовиться к их спасению: учиться выращивать в неволе, писать разъяснения для будущих жителей острова и пр. Но вот незадача - уникальных видов на острове слишком много. Как бы понять, для каких из них угроза истребления наиболее вероятна?" Что вы могли бы посоветовать д-ру Паганелю? Ваши умозаключения о том, какими свойствами обладают виды, для которых риск истребления наиболее велик, по возможности подтвердите примерами.