
1981 год.
1. Из утверждений
A делится на 2;
A делится на 2;
A делится на 12;
A делится на 24
три верных и одно неверное. Какое именно?
2. Написаны числа 0; 1; 0; 0. За один шаг разрешается прибавлять единицу к любым двум из них. Можно ли добиться, чтобы все числа стали равны?
3. Несколько ящиков вместе весят 10 тонн. Каждый не более одной тонны. Сколько трёхтонок заведомо достаточно, чтобы увезти этот груз?
1. Автомобилист проехал на 4-колёсной машине с одной запасной шиной 5000 км, меняя шины так, чтобы они изнашивались одинаково. Сколько километров прошла каждая шина?
2. Увадратная площадка 100 м * 100 м выложена квадратными плитами 1 м * 1 м четырёх цветов. Никакие две плиты одного цвета не имеют общей стороны или вершины. Сколько может быть плит одного из цветов?
3. Несколько ящиков вместе весят 10 тонн. Каждый не более одной тонны. Сколько трёхтонок заведомо достаточно, чтобы увезти этот груз?
1. Может ли быть трапецией 4-угольник со сторонами l=10, 11, 12, 13,
2. Дана периодическая дробь с периодом N.
Может ли этот период при умножении дроби на 2 или
при её делении на 2
а) увеличиться;
б) уменьшиться?
3. 50 человек за круглым столом. Им выдают 101 шар,
среди них 2k+1 чёрных. Первый получает 3 шара,
остальные по 2. Далее движение шаров по правилам: если человек имеет
после некоторого хода 3 шара одинакового цвета - игра прекращается,
если разного - оставляет себе 2 одинаковых, а один другого цвета отдаёт
соседу справа. Какое максимальное количество шагов может быть в игре, если
а) k=1;
б) 1<k<49?
1. Каждая изсторон a, b, c одного треугольника больше соответствующей ей стороны a1, b1, c1 другого треугольника. Верно ли, что площадь первого треугольника больше площади второго?
2. Имеется 10 пар чёрных и 10 пар коричневых перчаток. Берут наугад по одной перчатке. Сколько перчаток нужно взять, чтобы наверняка получить пару перчаток одного цвета?
3. Командир решил построить солдат в колонну по 4. При этом солдат Иванов остался лишним. Тогда командир приказал построиться по 5. И снова солдат Иванов остался лишним. Когда же в колонне по 6 Иванов остался лишним, командир посулил ему наряд вне очереди, после чего в колонне по 7 Иванов нашёл себе место и никого лишнего не осталось. Сколько солдат могло быть у командира?
4. На дороге, соединяющей два аула, нет ровных участков. Автобус едет в гору всегда со скоростью 15 км/час, а под гору 30 км/час. Найти расстояние между аулами, если путь туда и обратно без остановок занимает 4 часа.
1. Квадрат 10*10 на клетчатой бумаге. Двое по очереди режут прямыми по сетке. Один отрезает, одну из получившихся частей уничтожает, другую отдаёт другому. Тот делает тоже самое. Проигрывает тот, кому досталось 1*1. Кто выигрывает при правильной игре?
2. Есть 10 синих и 10 красных шариков. Каждым ходом можно забрать себе
несколько шариков одного цвета или несколько шариков одного цвета
(ранее забранных) положить обратно. Ходы делают двое по очереди.
Выигрывает тот, кто забрал все шарики? Кто выигрывает при правильной игре?
(Усложнение - больше цветов, 3 или 10).
3. 15-угольник. Каждым ходом разрезается по диагонали, получившаяся
часть с меньшим количеством сторон уничтожается, а другая - отдаётся сопернику.
Проигрывает тот, кому достался треугольник. Кто выигрывает - первый или второй?
(Вариант - 17-угольник).
4. Дано 15 орехов. Играют двое, ходят по очереди, ходящий забирает себе сколько-то орехов (>0), но менее половины. Проигрывает тот, кто не может сделать очередного хода (это бывает, если осталось два ореха). Кто выигрывает при правильной игре - начинающий или второй?
5. Часовая стрелка стоит на 12. Двое играющихпо очереди двигают её. Передвигать стрелку можно на 2 или на 3 часа вперёд. Выигрывает тот, кто поставил на 11. Кто выигрывает при правильной игре - первый или второй?
6. Написано число 1000000. Первый игрок пишет произведений двух
натральных чисел, больших 1, равное 1000000. Второй выбирает любой
сомножитель и под ним пишет равное ему произведение двух сомножителей.
И т. д. по очереди. Проигрывает тот, кто не смог сделать очередной ход.
Кто выигрывает при правильной игре - первый или второй?
(Вариант: выигрывает тот, кто не смог сделать очередной ход).
1. 25 спичек. Берут по очереди, каждый себе 1, 2 или 3 спички (облегчённый вариант: 1 или 2). Выигрывает тот, у кого в конце игры останется чётное число спичек. Кто выигрывает: начинающий или второй?
2. A - натуральное. Двое играющих по очереди разбивают все числа
имеющегося набора (при первом ходе весь набор - число A) на
натуральные слагаемые или на большие 1 натуральные сомножители.
За один ход разбивается одно число на 2 слагаемых или 2 сомножителя.
Проигрывает тот, кто не может сделать очередной ход.
Кто выигрывает при правильной игре?
а) A=10
б) A=11
1. Мальчик Лёва катался на лодке и с воды сфотографировал берег.
Когда он напечатал фотографии, то не смог понять, где изображение берега,
а где его отражение в воде. Укажите несколько возможных способов
это сделать.

2. Флатландия - это плоская страна. В ней существуют только два измерения. Как можно прикрепить колесо к автомобилю во Флатландии? (Сделать ось, как в трёхмерном мире, нельзя - ей некуда там торчать).
3. При проведении точных взвешиваний весы помещают под колпак, из-под которого откачан воздух. Зачем это нужно?
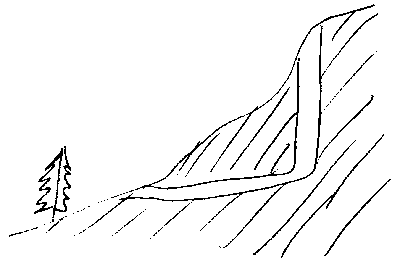
4. Михайло Ломоносов исседовал движение воздуха в шахтах сложного профиля.
В какую сторону будет сквозить зимой и летом в шахте, изображённой на рисунке?
1. Мальчик Серёжа смотрел телевизор и решил сфотографировать
заинтересовавшие его изображения. Когда он напечатал фотографии, то увидел
на них светлые и тёмные полосы. Почему? Что можно сказать об устройстве
затвора?
[Задача предполагалась, но была снята.]
2. Навстречу друг другу летят две одинаковые гантельки.
Они упруго сталкиваются.
Как будут разлетаться гантельки после того, как столкновение закончится?
Рассмотрите случаи v1=v2 и
v1=/=v2.

3. Груз падает на вертикальную пружинку. На какой высоте он будет иметь
максимальную скорость?
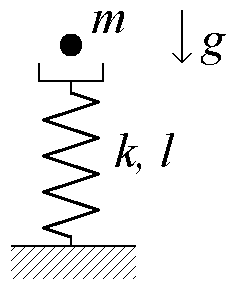
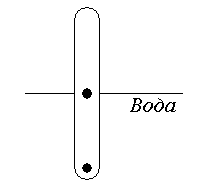
4. В пенопластовый поплавок спрятаны два кусочка свинца.
В каких слуаях поплавок будет:
1) тонуть:
2) торчать из воды;
3) опрокидываться на поверхность воды?
rпенопласта<<1
m1=m2.
1. Зажигаем спичку и держим её горизонтально. Сгорая, спичка изгибается вверх. Почему?
2. Нанизываем пуговицу на нитку, которую пропускаем туда-обратно. Затем устраиваем вертушку, разводя руки с надетыми на них петлями нитки. Оценить частоту вращения пуговицы.
3. Берём гибкую трубочку и опускаем один конец в сосуд с водой. Всасываем немного воды в трубку и опускаем другой конец ниже уровня воды в первом сосуде, но над другим сосудом. Из второго конца льётся вода, хотя трубка может подниматься своей средней частью достаточно высоко. Тогда поднимаем второй конец. Некоторое время вода ещё льётся, а потом прекращает. И если теперь вновь опустить второй конец, то она не польётся. Объяснить.
1. Измерение глубины труднодоступных рек долгое время было делом непростым. Однако теперь это умеют делать с помощью самолёта, верёвок, кирпича, двух поплавков и фотоаппарата. Как это?
2. Какие доводы можете вы привести скептику в доказательство того, что Земля - шар?
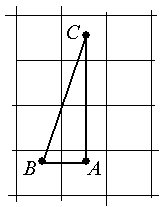
3. Туристы хотели побывать в трех пунктах (A, B, C).
Их маршрут на карте с нанесёнными меридианами и параллелями выглядит
треугольником. Кратчайший ли путь они выбрали?
1. Назовите ядовитые растения Подмосковья.
2. Назовите кустарники Подмосковья.
3. Назовите птиц, зимующих в Подмосковье.
4. Назовите птиц Подмосковья, гнездящихся в дуплах.
1. Какие существуют способы передвижения водных животных, непригодные для передвижения по суше?
2. Как выглядят плоды огородных растений: картофеля, капусты, моркови, гороха, петрушки, свёклы. Нарисуйте их.
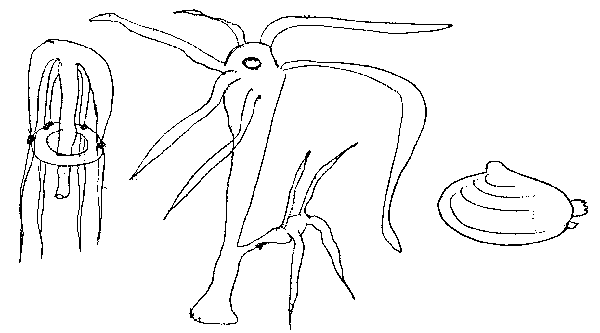
3. Какими способами, по вашему мнению, питаются водные животные,
изображенные на рисунке?
1. Чем удобна и чем неудобна для животных яркая окраска?
2. Какие преимущества получают растения, обладающие сочными плодами.
3. Почему вдоль дорог можно встретить растения, нехарактерные для данной местности?
4, 5 и 6 = 4, 5 и 6 для 8-9 кассов.
1. По каким причинам некоторые растения редки? Что нужно сделать для их охраны? Приведите примеры.
2. Почему в последние годы у нас остаются на зиму птицы, которые раньше улетали на юг? Назовите таких птиц.
3. Как питаются /способ и объект/ рыбы, изображённые
на рисунке?
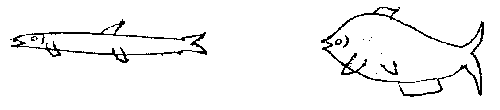
1. Какие преимущества даёт насекомым умение летать?
2. Известно, что, когда в средние впека в Европе появилась холера, смерть от неё наступала довольно быстро. В наше же время даже при отсутствии врачебного вмешательства смерть от холеры наступает гораздо позже. Чем можно объяснить такое изменение сроков протекания болезни?
3. Чем наружный скелет /например, раковина моллюска/ лучше и хуже внутреннего? Приведите примеры.
1. Почему большинство наших насекомоядных растений живёт на болотах?
2. Неким животным необходимо длительное время для переваривания пищи. Придумайте, какими способами это могло бы достигаться.
3. Известно, что у лягушек /например, травяной/ икра откладывается в течение недели, а превращение головастиков в лягушат длится всё лето. Чем это можно объяснить и какое биологическое значение может иметь это явление?
4. Какие проблемы возникают у животных в связи с выходом на сушу? Какие вы можете предложить способы их решения?
1. Какие животные создают запасы пищи и как они их используют?
2. Хорошо ли убирать из леса упавшие деревья и почему?
3. Где и почему больше видов птиц - в лесу или на опушке?
4. Как влияет снежный покров на жизнь растений и животных?
1. Какими способами растения могут воздействовать друг на друга?
2. Какими способами может достигаться плавучесть у водных животных?
3. Какими способами растения могут освобождаться от ненужных веществ?
1. Почему растения-сорняки мы обычно не находим в лесу, на лугу и на болоте?
2. Как количество водорослей изменяется с глубиной и почему?
3. Известно, что птицы, особенно тропические, попадая в зоопарки, теряют яркость окраски. Дайте объяснение этому факту.