Турнир им. Ломоносова 1995 года

На данной странице вы можете ознакомиться со следующей информацией:
(дата последнего обновления 12.12.1998)
Страница находится в стадии разработки.
Все ответы и решения будут размещены здесь через некоторое время.

Конкурс по математике

Задачи

  1. (7-11) На плоскости расположен квадрат, и невидимыми чернилами нанесена точка. Человек в специальных очках видит точку. Если провести прямую, то он говорит, лежит ли точка на прямой, а если не лежит, то говорит, по какую сторону от этой прямой лежит невидимая точка. Какое наименьшее число прямых необходимо провести, чтобы узнать, лежит ли невидимая точка внутри квадрата (не снаружи и не на границе)?
  2. (7-9) Существует ли 100 натуральных чисел таких, что их сумма равна их наименьшему общему кратному?
  3. (7-9) Прямоугольник ABCD (AB=a, BC=b) сложили так, что получился пятиугольник площади S (C легла в A). Докажите, что S< 3/4ab.
  4. (10-11) Ma, Mb, Mc - середины сторон, Ha, Hb, Hc - основания высот треугольника ABC площади S. Доказать, что из отрезков MaHb, MbHc, McHa можно составить треугольник, найти его площадь.
  5. (10-11) а) Существует ли четыре таких различных натуральных числа, что сумма любых трех из них есть простое число?
    б) Существуют ли пять таких чисел?

Решения задач конкурса по математике

  1. (7-11)Ответ: необходимое и достаточное число вопросов - три.

    Достаточность. Пусть наш квадрат - ABCD. На первом шагу проводим прямую AC. Человек в специальных очках (для краткости - "человек" ) указывает одну из полуплоскостей или саму прямую. Если это - полуплоскость, содержащая вершину B, то на втором и третьем шагу проводим прямые AB и CB. Те же прямые проводим и в том случае, если он указывает на саму прямую AC. Если на втором и третьем шагу человек указывает оба раза ту полуплоскость, в которой лежит треугольник ABC, то невидимая точка лежит строго внутри квадрата; если один раз он указывает на эту полуплоскость, а второй раз - на прямую, или оба раза - на прямую, то точка лежит на границе квадрата. Если хотя бы один раз он укажет на полуплоскость, в которой нет треугольника ABC, то точка лежит вне квадрата. Случай, когда человек укажет на полуплоскость, содержащую точку D, аналогичен.

    Необходимость. Если задано всего один или два вопроса, то проведено меньше трех прямых (две или одна). Каковы бы ни были ответы, мы можем узнать только, принадлежит ли точка тем частям, на которые плоскость разбита проведенными прямыми. Но эти части неограничены, и принадлежность им не может быть доказательством того, что точка принадлежит квадрату.

  2. (7-9)Такие числа существуют. Вот один из примеров:
    1, 1, ..., 2, 2, ..., 4, 5, 6 (89 единиц, 8 двоек). Сумма этих чисел ( S ) равна 120, и наименьшее общее кратное (НОК) - тоже 120.

    Задачу можно было понять и так, что все числа должны быть различны. Вот пример такого набора:
    1, 3, 4, 8, 16, ..., 3*298, 299 (последовательные степени двойки, но на втором месте стоит 3, а на 99-м - 3*298 ). Для этих чисел НОК = S = 3*299.

  3. (7-9) Нарисуем на прямоугольнике прямую l, по которой его сложили. Чтобы точка C совпала с точкой A, нужно, чтобы l проходила через середину диагонали AC и была ей перпендикулярна. Известно, что получился пятиугольник, следовательно, наш прямоугольник - не квадрат. Допустим для определенности, что AB< CD. Тогда l пересекает стороны BC (в точке M) и DA (в точке N). AMN=CMN, так как они совпали при наложении. Отсюда CM=MA, CN=NA, /MCA = /MAC, /NCA = /NAC. Но /DAC = /BCA, так как AD || BC. Следовательно, CMA и CNA - равные между собой равнобедренные треугольники. Отсюда, MA=ND, /CND = /AMB и, следовательно, CND=AMB.

    Разобьем наш четырехугольник на четыре треугольника: ABM, AMN, CMN и CND. Площади первого и четвертого из них равны, и площади первого и второго тоже равны, при этом SABM< SAMN (у них общая высота AB, при этом основание AN треугольника AMN больше основания BM треугольника ABM). Значит, площадь треугольника AMN составляет больше, чем четверть от площади четырехугольника.

    Пятиугольник, который получился после того, как четырехугольник сложили, состоит из треугольников ABM, CND и AMN (или CMN). Мы видим, что из четырехугольника выбросили кусок, который по площади больше четверти площади четырехугольника. Это значит, что осталось меньше, чем 3/4.

  4. (10-11) Треугольник BCHb - прямоугольный, точка Ma - середина его гипотенузы, которая, как известно, совпадает с центром описанной вокруг треугольника BCHb окружности. Поэтому |MaHb|=|MaB|=1/2BC.

    Аналогичные рассуждения относительно двух других указанных в условии отрезков показывают, что
    |MbHc|=1/2AC, |McHa|=1/2AB. Таким образом, из указанных отрезков можно составить треугольник, стороны которого вдвое меньше сторон исходного треугольника. Такой треугольник подобен исходному с коэффициентом подобия 1/2, и его площадь равна S/4.

  5. (10-11) а) Ответ - существуют. Вот пример такой четверки чисел: 1, 3, 7,9. Из этих чисел можно образовать четыре тройки; их суммы - 11, 13, 17 и 19 - числа простые.

    б) Ответ - не существуют. Целое число при делении на три может дать один из трех остатков: 0, 1, 2. Сумма трех целых чисел, дающих одинаковый остаток при делении на три, сама делится на три. Если имеются три целых числа такие, что их остатки при делении на три все различны, то сумма этих чисел также делится на три. Допустим теперь, что имеется набор из N различных натуральных чисел такой, что сумма любых трех из них - число простое. Во-первых, заметим, что эта сумма всегда не меньше 6, так как числа все положительны и различны, следовательно, чтобы эта сумма была простым числом, она не должны делиться на три. Из этого следует, что среди остатков при делении на три всех чисел набора не могут встретиться все три варианта (доказано выше), а каждый из двух оставшихся вариантов может быть представлен не более, чем двумя числами. Отсюда следует, что N < 4.

Конкурс по математическим играм

Условия игр

  1. Двое по очереди пишут цифры, начиная с ненулевой, со старшего разряда (по порядку вплоть до младшего). Всего - 6 цифр. Если число разделится нацело на 7, то выигрывает сделавший последний ход, иначе - начинающий. Кто выигрывает при правильной игре?
  2. Двое по очереди пишут цифры, начиная с ненулевой, со старшего разряда (по порядку вплоть до младшего). Всего - k цифр. Если число разделится нацело на 11, то выигрывает сделавший последний ход, иначе - начинающий. Кто выигрывает при правильной игре? Рассмотреть случаи:
    а) k - четно; б) k - нечетное, большее 1.
  3. Двое по очереди ставят коней на шахматную доску. Нельзя ставить коня под бой хотя бы одного из ранее поставленных. Кто не может поставить коня, проигрывает. Кто выигрывает при правильной игре?
  4. Каждым ходом из лежащих на столе конфет можно взять любое число, строго меньшее половины, или ровно одну конфету. Выигрывает тот, кто взял последнюю конфету. Кто выиграет при правильной игре, если на столе - 50 конфет.
    Замечание: лучше сначала разобраться с 2, 3, 4, ... конфетами.
  5. Есть несколько яблок и 2 человека. Они берут по яблоку и начинают есть одновременно. Каждый иожет взять следующее яблоко только после того, как съел предыдущее. Скорость поедания (в граммах в секунду) одинакова у обоих игроков. Какое яблоко стоит выбрать первому подошедшему к столу, чтобы съесть больше в следующих случаях:
    а) 3 яблока: 300 гр, 400 гр, 500 гр;
    б) 300, 500, 700, 900;
    в) 300, 600, 700, 800;
    г) 10, 20, 21, 30, 31;
    д) 100, 201, 202, 203;
    е) 201, 299, 400, 600, 900;
    ж) a, b, c, d, где a < b < c < d и d < a+b.
  6. В клетки прямоугольника а) k на k; б) 2 на k по очереди ставят прожектора, освещающие все клетки, расположенные не левее и не выше. При этом каждым ходом надо освещать хоть одну новую клетку. Кто поставит прожектор в самый левый верхний угол, проигрывает. Кто может обеспечить себе выигрыш, и как ему следует играть?
  7. Философы Тун и Бол начали спор, выдвинув по одному тезису каждый. Далее по очереди каждый может либо повторить, без пропуска, абсолютно все свои ранее произнесенные фразы или же повторить только что прослушанную речь другого, добавив к ней одну свою фразу. Проигрывает тот, кто впервые в очередном своем выступлении произнесет более 9 фраз подряд. Кто переспорит?

Выигрышные стратегии

  1. ПЕРВОЕ РЕШЕНИЕ: второй последним ходом всегда может сообразить, поделив в столбик, какую цифру надо написать, чтобы полученное число разделилось на 7 (если предпоследнее (пятизначное) число равно A и остаток от деления на 7 числа 10A есть r, то нужно дописать цифру 7-r).

    ВТОРОЕ РЕШЕНИЕ: второй может каждым ходом, пользуясь таблицей умножения на 7, автоматически дописывать после 1 - 4, после 2 - 1, после 3 - 5, и так далее. Получится число вида abcdef, где ab, cd и ef делятся на 7, откуда и само число тоже делится на 7.

  2. а) Второй копирует цифры первого. Получается число вида aabb...cc, которое делится на 11.

    б) Выигрывает опять второй. Надо добиться ситуации a(a-1)bbcc\ldots dd*. Какую бы цифру вместо звездочки ни поставит первый, делиться на 11 не будет.

  3. Выигрывает второй (симметричная стратегия (относительно диагонали, или относительно центра)).

  4. Замечание: предлагалось разобраться с 2, 3, 4, ... конфетами.

    Второй выигрывает при числе конфет 2, 4, 16, 32, 64, ..., поскольку из не степени двойки всегда можно получить степень двойки, а из степени двойки (кроме числа 2) можно получить только не степень двойки. Таким образом, при 50 конфетах выигрывает первый.

  5. Ответы:
    а) первый, брать 300
    б) первый, брать 300 или 500
    в) первый, 600
    г) первый, 10
    д) первый, 201
    е) первый, 400
    ж) ничья при a+d=b+c; иначе выигрывает первый:
    при a+d > b+c брать d, при a+d < b+c брать b.

  6. Ответы:

    а) Выигрывает первый. Первым ходом освещаем максимальный квадрат, не совпадающий с данным. Далее - симметричная стратегия.

    б) Выигрывает первый. Примените индукцию. Первый ход - в правую нижнюю угловую клетку. Далее первый может каждым ходом возвращать доску в состояние "прямоугольник без угловой клетки".

    Замечание: можно доказать, что для любого прямоугольника всегда выигрывает первый. Действительно, пусть второй имеет выигрышную стратегию. Заметим, что при любом начальном ходе правая нижняя клетка всегда освещается. Поэтому если первый первым ходом делает ход в правый нижний угол, то любой ход второго приведет к тому же результату, если бы первый до этого не ходил. Поэтому первый сможет теперь применить стратегию второго и выиграть. Полученное противоречие показывает, что выигрывает всегда первый (но явной стратегии из этого решения не извлечешь).

  7. Указание: искусственная переборная задача. Выигрывает первый, сказав первым ходом 2 фразы (дальнейшее решение - перебор вариантов). Можно разобрать случаи с другим количеством фраз.

Конкурс по физике

Задачи

(В скобках указаны классы, для которых рекомендована задача, но засчитывались все решенные задачи.)

  1. (7-9) Недавно в средствах массовой информации прошло сообщение о гигантском айсберге, оторвавшемся от ледяного панциря Антарктиды. Размеры айсберга примерно 100 км в длину, 10 км в ширину и 1 км в толщину. Экологи бьют тревогу. На сколько повысится уровень Мирового океана, когда айсберг растает?
  2. (7-9) Известный изобретатель вечных двигателей Презентов заканчивает сборку последней модели. Как известно, по капиллярам в деревьях сок может подниматься очень высоко. Берем бревно, опускаем в воду, вода поднимается вверх. Вверху вода по специальным срезам сбоку (вспомним сбор березового сока) поступает в желобки и оттуда льется на мельничные колеса, приводя их в движение. Почему же этот двигатель все же не работает?
  3. (7-11) Какое время суток изображено на картине Врубеля "Пан"? Определите с возможной точностью время.
  4. (10-11) Празднуя удачную посадку на Луну, члены экипажа лунохода,прямо в кабине, где они находились без скафандров, открыли бутылку "Боржоми". Чем отличалось поведение пузырьков в этой бутылке от пузырьков в такой же бутылке, но открытой на Земле?
  5. (10-11) Нобелевская премия по физике за 1993 год была вручена Дж.Тейлору и Р.Халсу за открытие в 1974 году первого двойного пульсара. Они обнаружили, что интервал между импульсами от пульсара (вращающейся вокруг оси нейтронной звезды, у которой есть излучающее "горячее пятно", несовпадающее с полюсом; как только луч от "горячего пятна" попадает на Землю, фиксируется импульс) периодически слабо меняется и объяснили это тем, что излучающая импульсы нейтронная звезда вращается вокруг другой нейтронной звезды. Объясните, как именно меняется интервал между импульсами по мере обращения звезд друг относительно друга и как можно оценить радиус орбиты этого вращения.
  6. Оцените, на сколько может повыситься температура в этой аудитории от Вашего пребывания в ней.

Решения задач конкурса по физике

В решениях, предложенных школьниками, Жюри ценило прежде всего умение увидеть главные особенности явления и пренебречь второстепенными. Что является главным и что второстепенным, это на первых порах определяется чисто интуитивно. Чтобы подтвердить или не подтвердить правильность интуитивных предположений, требуется более подробно рассмотреть явление. При более подробном рассмотрении часто требуются новые интуитивные предположения, и так, строго говоря, до бесконечности. Практически нужно остановиться в тот момент, когда интерес к поставленной задаче удовлетворен. Таким образом, требования к решению школьника не являются строго определенными, и немалую роль играет совпадение или несовпадение вкусов и традиций учащихся и членов жюри. Поэтому и оценки решений не бывают строго объективными. Однако не это главное. При подборе задач мы старались дать материал для размышлений, который помог бы лучше понимать и чувствовать окружающий нас реальный мир, а это было бы полезно учащимся независимо от того, какой род деятельности они выберут для себя в дальнейшем.
  1. Сообщения в средствах массовой информации, о которых говорится в задаче, действительно имели место. Мы не назвали газеты, в которых они были напечатаны, и не указали авторов (хотя могли бы, но зачем?). Замечу, что "экологи", которые упоминаются в задаче, это именно "экологи" в кавычках, то есть часто малограмотные в науках представители общественных и политических движений. Это я пишу в порядке извинения перед настоящими экологами (без кавычек) - специалистами в конкретной и очень интересной биологической дисциплине.

    В порядке извинения перед школьниками и учителями замечу, что предложенная задача стара, как мир. Во многих задачниках она предлагается в форме: "В стакане воды плавает кусочек льда ..." и т.д., продолжение очевидно. Формулировки, понятно, эквивалентны, но есть решение, которое более естественно выглядит для стакана.

    В этой задаче ответ - уровень не изменится. Это легко получить из закона Архимеда. Вес вытесненной воды равен весу льдины. В результате таяния льда его вес не изменится, и растаявшая вода займет тот же объем, который занимала подводная часть айсберга.

    Другое решение я формулирую для стакана. Предположим для простоты, что стакан - цилиндрический. Поставим стакан с водой и льдинкой на весы. Они покажут общий вес этих предметов. Понятно, что когда лед растает, вес не изменится. Вес воды с плавающими в ней предметами равен давлению воды на дно стакана, умноженному на площадь дна. Давление определяется высотой столба воды. Раз давление не изменилось, то и высота столба не изменилась.

    Это - решение в первом приближении. Уточним, что нужно предположить, чтобы это решение было верным. Мы предположили, что
    а) присутствие воздуха над водой пренебрежимо;
    б) температура воды и льда одинакова и равна 0 градусов;
    в) вода и лед чистые.

    Подробное рассмотрение задачи, когда эти условия не выполнены, приводит к очень незначительному уточнению ответа: оказывается, что при реальных значениях давления воздуха, температуры и солености воды уровень почти не меняется.

    Предлагаем учащимся оценить влияние указанных факторов. Можете ли вы назвать еще какие-нибудь факторы, способные изменить ответ?

  2. Если бы сок в деревьях поднимался только под влиянием капиллярных сил, то, во-первых, он поднимался бы очень невысоко, а во-вторых, он никогда не выливался бы из верхнего конца капилляра (вспомните, как возникает сила, поднимающая жидкость в капиллярном сосуде - для возникновения подъемной силы необходимо, чтобы над мениском продолжались стенки сосуда). В живом дереве сок поднимается под действием нескольких механизмов. Один из них - осмотическое давление, которое возникает вследствие высокой концентрации солей внутри дерева, в то время, как концентрация солей в почве значительно ниже. Этот механизм может привести к выливанию сока из сосуда, но он не дает возможности создать вечное движение, так как концентрацию солей нужно как-то поддерживать. В живом дереве ее поддерживают биохимические реакции. Другие механизмы подъема соков связаны с наличием специальных органов, расположенных на стволе дерева. Эти органы работают также только на живых деревьях.

    Впрочем, г. Презентов еще не закончил испытания своей машины, так что последнее слово еще не сказано.

  3. Время суток можно определить, зная положение и форму Луны на небе. Известно, что Луна вращается вокруг Земли, которая, в свою очередь, вращается вокруг Солнца, а также вокруг своей оси (рис. 1).


    Рисунок 1.

    Плоскости вращений Земли вокруг Солнца и Луны вокруг Земли практически совпадают. Плоскости вращения Земли вокруг Солнца и вокруг своей оси не совпадают (между ними угол 23o27'). Направления всех трех вращений совпадают. Солнце всегда освещает половину Луны, обращенную к нему (кроме случая лунного затмения).

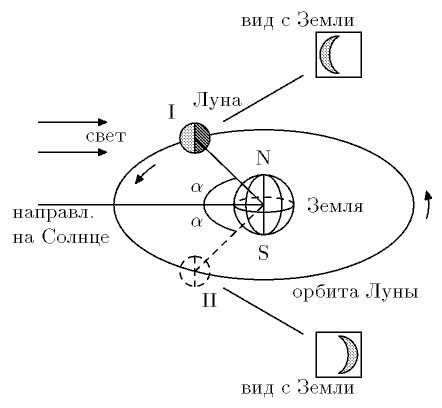
    Наблюдая Луну с Земли, мы видим только кусок освещенной части (серп). Толщина серпа зависит от взаимного расположения Луны, Земли и Солнца так:
    d=R(1 - cos a ) (см. рис. 2).


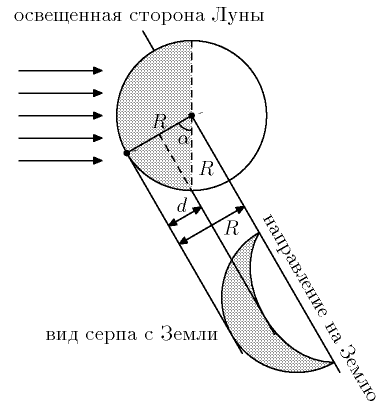
    Рисунок 2.

    У месяца на картине Врубеля d=R/2, откуда находим, что a=60o.

    Очевидно, что Врубель на своей картине изобразил пейзаж средних широт северного полушария.

    При известном угле a (то есть при известной форме Луны) возможны два положения Луны, обозначенные на рисунке 1 римскими цифрами I и II. Чтобы выяснить, какое из них имеет место, заметим, что (если смотреть из северного полушария) в положении I концы серпа обязательно направлены вправо (убывающая Луна), в положении II - влево (растущая Луна). Так как серп на картине обращен вправо, то Луна находится в положении I.

    На рисунке 3


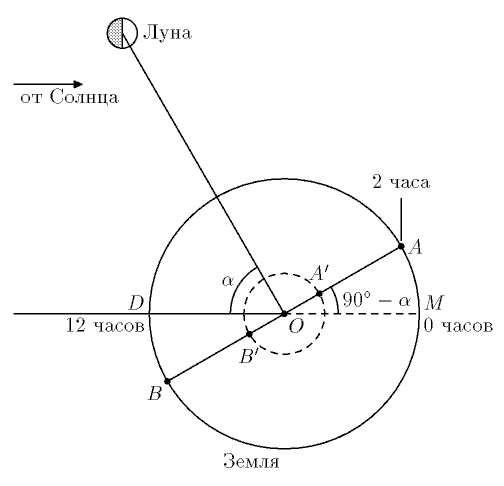
    Рисунок 3.

    плоскость бумаги совпадает с плоскостью, содержащей центры Солнца, Земли и Луны, но не совпадает с плоскостью экватора Земли. Внутри круга, изображающего проекцию Земли на плоскость чертежа, нарисована пунктирная окружность, на которой находится северный полюс Земли. В какой именно точке этой окружности он находится, зависит от времени года.

    Далее, Луна находится на линии горизонта, то есть направление на нее касается поверхности Земли в точке наблюдения. Значит, действие на картине происходит где-то на линии АВ чертежа вне пунктирной окружности и на северной стороне Земли либо со стороны точки А, либо со стороны точки В (отрезки AA' и BB' соответственно). Если действие картины происходит на отрезке BB', то ось серпа (прямая, соединяющая его концы) должна быть повернута по часовой стрелке на некоторый угол; если же на отрезке AA', то эта ось повернута против часовой стрелки (см. рис. 4).


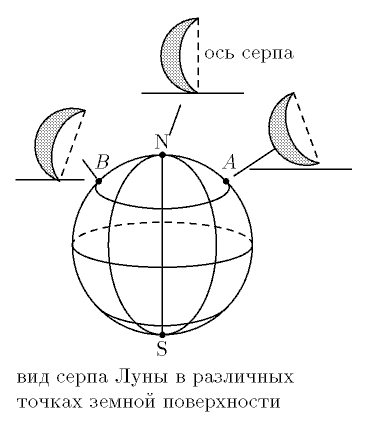
    Рисунок 4.

    На картине она повернута против часовой стрелки. Следовательно, картина изображает место, лежащее на отрезке AA' (отрезок BB' не годится также и потому, что там - день, и поэтому Луна не может быть видна достаточно четко).

    Легко рассчитать, какое было бы время, если бы северный полюс совпадал с точкой О (то есть экватор находился бы в плоскости рисунка 3). В точке D - 12 часов дня по местному времени, в точке M - 0 часов. Земля вращается против часовой стрелки. Угол AOM = 90o - a = 30o. Местное время зависит от угла линейно. Поэтому в А будет 12*30/180 = 2 часа.

    Несовпадение плоскостей вращения Земли вокруг Солнца и вокруг своей оси приводит к отклонению ответа от этого значения. Летом и весной это время уменьшается, зимой и осенью - увеличивается на час-полтора. Чем севернее местность, тем больше будет расхождение. Эти оценки можно сделать, рассматривая рисунок 3 и различные варианты расположения северного полюса на пунктирной окружности.

    Определить время с большей точностью не представляется возможным, исходя только из данных задачи.

  4. Давление в кабине было равно атмосферному, однако вес предметов был меньше, чем на Земле. Это значит, что на поверхности воды в открытой бутылке давление было атмосферное, а на дне бутылки - меньше того, какое было бы на Земле в этой же точке. Поэтому на Луне пузыри в толще воды будут выделяться более бурно. При этом они будут медленнее подниматься, так как архимедова сила будет меньше, чем на Земле. В итоге вода в бутылке вспенится сильнее, чем на Земле.

  5. Из двух нейтронных звезд нас интересует та, которая излучает. Она движется вокруг общего центра масс двух звезд по некоторой орбите; предположим для простоты, что орбита - круговая. Предположим также сначала, что наблюдатель расположен в плоскости этого вращения, и расстояние от центра вращения до точки наблюдения (до Земли) постоянно и равно D. Линейную скорость вращения звезды обозначим через V, время между соседними импульсами - через d.

    Обозначим через А точку орбиты, в которой звезда с максимальной скоростью движется на нас; это бывает, когда угловое расстояние звезды от центра вращения максимально (с точки зрения наблюдателя); скорость приближения звезды к наблюдателю в этой точке равна V. Рассмотрим импульс, который излучила звезда, находясь в точке А (момент его излучения примем за начало отсчета времени), и следующий импульс, излученный через время d. Время, в течение которого первый импульс дошел до наблюдателя, равно D/c (c - скорость света). Время, в течение которого следующий импульс дошел до наблюдателя, меньше, так как источник излучения находится ближе к наблюдателю на величину Vd. Это время равно (D-Vd)/c. Итак, импульсы фиксируются наблюдателем в моменты: D/c и d+(D-Vd)/c. Разность между этими моментами есть наблюдаемое время между импульсами d-. Оно равно d- = d + (D-Vd)/c - D/c = d(1-V/c).

    Рассмотрим точку В орбиты, в которой звезда с максимальной скоростью удаляется от наблюдателя. Аналогичный расчет дает, что наблюдаемое время между импульсами в этом положении звезды d+ = d(1+V/c).

    Среднее значение d+ и d- равно (d+ + d-)/2 = d. d+ и d- - наблюдаемые величины, тем самым величину d можно считать известной. d+ - d = V/c; тем самым и величину V можно вычислить. Период Т обращения звезды вокруг общего центра вращения двух звезд мы также знаем, так как это - наблюдаемая величина. Длина орбиты равна s = VT. В то же время s = 2pR. Отсюда находим R.

    Замечу, что рассмотренный эффект изменения частоты излучения при движении источника относительно наблюдателя есть хорошо изученный и разобранный в учебниках эффект Доплера.

    Итак, в некоторых добавочных предположениях задача решена. Этих предположений два: неподвижность звезды относительно точки наблюдения (точнее - постоянство расстояния до нее) и расположение наблюдателя в плоскости вращения звезды. Если отбросить эти предположения, то результаты расчета изменятся.

    Пусть звезда, например, приближается к нам со скоростью v. Тогда из тех же рассуждений мы получим, что наблюдаемый интервал между соседними импульсами в точках А и В равен соответственно d(1-(v+V)/c) и d(1-(v-V)/c), а среднее значение этих интервалов равно d(1-v/c). То же получится, если двойная звезда удаляется от нас (в этой формуле v будет отрицательное). Если скорость приближения или удаления двойной звезды от наблюдателя каким-то образом найдена, то можно найти величину d. Если же она неизвестна, то найти d невозможно.

    Отбросим теперь второе предположение. Пусть угол между отрезком, соединяющим точку наблюдения и общий центр двойной звезды, и осью вращения излучающей звезды относительно центра вращения отличен от прямого и равен a. Тогда в нашем расчете V заменится на
    V cos a. В остальном расчет сохранится. Но если a неизвестен, то довести расчет до численного результата невозможно. Заметим лишь, что cos a всегда не больше 1, поэтому мы получим для радиуса вращения ограничение снизу. Если, не зная угла a, мы примем его за p/2, то получим радиус вращения, который может оказаться больше истинного, но никак не меньше.

  6. Отбросим шуточные ответы вроде такого, который начинается словами: "Поскольку в Государственной Академии Нефти и Газа не топят, я совсем замерзла и не способна выделять тепло... ".

    В этой задаче главное - найти зацепку, позволяющую получить хотя бы неточный, но численный ответ. Многие учащиеся заметили, что основным механизмом выделения тепла является дыхание. Оценить теплоотдачу через дыхание сравнительно несложно. Примем, что человек делает в спокойном состоянии 20 вдохов и выдохов в минуту, каждый раз вдыхая 1 литр воздуха. Это значит, что за час он выдыхает 20*60*1 = 1200 литров воздуха. При этом температура выдыхаемого воздуха почти равна температуре тела, то есть 36o C. Считая для простоты, что температура воздуха в аудитории равна 16o, получаем, что 1200 литров воздуха нагреты на 20o. Если аудитория имеет объем 1000 кубометров (каждый учащийся может на глаз оценить размеры своей аудитории), то получим, что 1/800 часть воздуха нагрелась на 20o, следовательно, если весь воздух перемешать, то его температура повысится на 20/800 = 1/40 градуса.

    Обсудим теперь, насколько правомерно считать, что дыхание - основной механизм теплоотдачи. Скорее всего - такое предположение все же неверно. Если бы теплоотдачей с поверхности тела можно было пренебречь, то незачем было бы тепло одеваться. Но можно ли считать, что теплоотдача через поверхность тела - главный механизм теплоотдачи организма, а дыханием можно пренебречь? Вспомним, как ведут себя в жаркую погоду собаки. Даже те, у которых очень теплый мех, могут добиваться для себя нормальной температуры. Для этого они часто дышат, высунув язык. Из этого примера видно, что дыхание в некоторых случаях может быть главным и почти единственным способом охлаждения тела. Отсюда можно сделать вывод, что для человека оба механизма скорее всего дают одинаковый по порядку величины эффект.

    Итак, ответ задачи 1/20 градуса (для принятых размеров аудитории).

Конкурс по химии

Задачи

  1. Химический анализ соединения азота с водородом, имеющего относительную массу 32, показал, что массовая доля азота в соединении равна 66% . Докажите, что результаты анализа неверны.
  2. В замкнутый объем поместили два одинаковых стакана с температурой 25оС с дистиллированной водой и раствором серной кислоты (массовая доля 80%). Что можно сказать о температуре каждого из стаканов через некоторое время?
  3. При обработке ультрасветовым излучением смеси крахмала, водного раствора йодида калия и тетрахлорида углерода наблюдается появление синего окрашивания. Предложите объяснение этому явлению.
  4. Могут ли растворы двух солей, образованных одной и той же кислотой, изменять фиолетовую окраску лакмуса: одна в синий, другая - в красный цвет? Дайте мотивированный ответ и обсудите возможные варианты с конкретными примерами.
  5. Можно ли, имея тяжелую воду, получить LiAlD4 и (ND4)2SO4*FeSO4*6H2O? Приведите соответствующие реакции. Попробуйте получить продукты с максимальным выходом.
  6. Эквимолярную смесь азота и кислорода в замкнутом сосуде подвергали длительному воздействию электрического разряда, после чего продукты реакции привели к нормальным условиям и при интенсивном перемешивании добавили в избыток раствора карбоната натрия; причем в растворе после смешения (раствор А) нитрат-ионы обнаружены не были. Объем газов, оставшихся после этой операции, составлял 5/8 объема исходной смеси (измерения проводились в одинаковых условиях).
    1) В форме каких соединений находится азот в растворе А? Запишите необходимые уравнения реаRкций.
    2) Определите, если это возможно, какая часть азота прореагировала при воздействии разряда. Растворимостью газов в воде пренебречь.
  7. Необходимо обнаружить "химический след" находящейся на боевой позиции подводной лодки, неподвижно лежащей на глубине 60 м. Лодка выбрасывает за борт 2 кг/час отработанных смазочных материалов и 10 м3/час водорода, получающегося одновременно с используемым для дыхания экипажа кислородом. В результате коррозии лодка теряет 0.1 кг/час железа в виде Fe(II) и 0.5 кг/час используемого для защиты от коррозии цинка. Какие аналитические приборы и оборудование Вы считаете целесообразным установить на противолодочном корабле, в задачу которого входит обнаружение подводной лодки по ее "химическому следу" ?


Решения задач конкурса по химии

  1. Известно, что число атомов, вообще, и в молекуле, в частности, - целое число (слово "атом" в переводе с греческого означает "неделимый" ).

    По результатам анализа

    N(N) = 32*0,66*1/14 приблизительно равно 1,5

    Число атомов азота не может быть дробным, следовательно, анализ неверен.

  2. Стакан с водой будет иметь температуру, меньшую чем стакан с раствором серной кислоты. Стакан с H2SO4, которая является сильным гигроскопическим веществом, т.е. хорошо поглощает воду, будет нагреваться вследствие поглощения паров H2O (которые испаряются, а затем диффундируют из стакана с H2O).

    Стакан с H2O будет слегка охлаждаться за счет испарения воды.

  3. Напишем ряд химических уравнений, объясняющих данное явление:
    KJ ->hn K+ + I-
    2I- -> I2
    CCl4 + K+ -> KCl + CCl3* (свободный радикал)
    2CCl3* -> C2Cl6

    Окрашивание крахмала происходит под действием свободного J2

  4. Возможны варианты. Принципиально различаются 2 случая.

    1) KH2PO4 и K3PO4
    H2PO4- = H+ + HPO42-, -pH < 7
    PO43- + H2O = OH- + HPO42-, -pH > 7

    2) KCH3COO и Al(CH3COO)3
    KCH3COO : CH3COO- + H2O = OH- + CH3COOH, -pH > 7
    Al(CH3COO)3 : Al3+ + H2O = H+ + Al(OH)2+, pH < 7

  5. Получить LiAlD4 можно. Приведем соответствующие реакции:
    D2O -> D2 + 1/2O2 (электролиз)
    D2 + 2Li -> 2LiD
    4LiD + AlCl3 -> LiAlD4 + 3LiCl

    Получить (ND4)2SO4*FeSO4*6H2O не удается. Причина в том, что получить соль Мора можно совместной кристаллизацией сульфатов аммония и железа. Так как перед этим ион ND4+ будет находиться в растворе в присутствие H2O (которая, по предположению, перейдет в кристаллизационную, но воду), то будет происходить обмен
    ND4+ + H2O = ND3H+ + HDO .

  6. Возможны реакции
    N2 + O2 -> 2NO
    2NO + O2 -> 2NO2

    При поглощении раствором CO32-:
    1) H2O + NO+ NO2 + 2CO32- -> 2HCO3- + 2NO2-
    2) 4NO2 + O2 + 2H2O + 4CO32- -> 4HCO3- + 4NO3-

    Случай 2) невозможен. Значит, смесь газов до поглощения - NO, NO2 и, возможно, N2. После поглощения - N2 + NO.

    Пусть, в расчёте на 1 моль смесь (0,5 моль N2 и 0,5 моль O2) получилось x моль NO2.

    Имеем:

    Количество N: 2x + y + 2z = 1

    Количество O: 3x + y = 1

    Соотношение объемов y+z=5/8

    Отсюда y=11/20, x=3/20, z=3/40.

    Прореагировало 1/2-3/40=7/40 моль N2 из 0,5. Значит, прореагировало 70% N2.

  7. Подойдут любые разумные методы аналитического определения H2, Zn2+ и Fe2+. Для H2 - определение redox-потенциала воды, для Zn2+ сульфидный метод, для Fe2+ - [Fe(соль)]3-. Наиболее перспективен метод, основанный на обнаружении наличия смазочных веществ, например, с помощью адсорбентов или анализе поверхностного слоя воды на наличие органических примесей.

Конкурс по биологии

Вопросы

  1. Как общаются водные животные?
  2. Какие организмы умеют светиться? Зачем им это нужно?
  3. Чем объяснить разнообразие клювов у птиц?
  4. Что такое регенерация? У каких животных она развита лучше? Чем можно это объяснить?
  5. Какие функции выполняют млечники (смоляные ходы) у растений, и как человек использует млечный сок (смолу) разных растений?
  6. Предложите биологические методы изучения чистоты водоемов?
  7. В каких областях биологии и для каких целей применяется математика?
  8. Сколько рёбер у мужчин, а сколько у женщин?
  9. Какие организмы (возможно устойчивые симбиозы) могут являться одновременно:
    а) продуцентами и консументами
    б) продуцентами и редуцентами
    в) редуцентами и консументами
    г) теми, другими и третьими?

    Продуценты - организмы, создающие органические вещества из неорганических (зеленые растения, водоросли и некоторые микроорганизмы); консументы - организмы, питающиеся готовым органическим веществом; редуценты - разлагают органическое вещество до минеральных.

  10. Почему в клетке глюкоза хранится в виде полимеров (крахмал, гликоген, целлюлоза), а не в виде мономеров - простых сахаров?

Ответы на вопросы конкурса по биологии

  1. В основном водные животные общаются теми же способами, что и их сухопутные родичи. Для общения используются звуки, запахи, прикосновения, колебания среды, позы, жесты и другие зрительные стимулы, а также различные изменения в окружающей среде (например, содранная кора, следы и т.п.). Разница только в большей или меньшей степени развития всех этих способов. Так для водных животных часто большое значение имеют звуковые сигналы, так как звук хорошо распространяется в воде. Многие школьники писали об использовании некоторыми водными животными ультразвуков, и такой ответ (особенно если он был подкреплен примерами), засчитывался как верный. Хотя и этот способ вовсе не является уникальным для водной среды.

    А вот зрение водные обитатели используют значительно меньше, чем наземные. Это объясняется тем, что видимость в воде, как правило, гораздо хуже, чем на воздухе.

    Не следует путать общение животных с ориентацией в пространстве. Так многие водные животные используют эхолокацию для определения расстояния до каких-нибудь предметов, однако способом общения это, конечно, считать нельзя.

  2. Способность к свечению свойственна многим живым организмам. Перечислить их всех практически невозможно. При оценке ответа на этот вопрос учитывалось количество и правильность приведенных примеров.

    Наиболее известными светящимися существами являются светляки. Это насекомые, относящиеся к отряду жесткокрылых, т.е. жуков. У светляков способность к свечению помогает им в выборе и привлечении брачного партнера. У разных видов конкретный механизм и сигналы связи "самец-самка" различны. У наиболее обычного в наших краях Большого светляка самка светится гораздо сильнее самца. Она не имеет крыльев. Ее активный летающий партнер находит ее по яркому огоньку.

    Другой пример, часто встречающийся в работах школьников, это глубоководные рыбы вроде удильщика, которые используют светящиеся органы для приманивания добычи. Кстати говоря, этот прием используют не только рыбы, но и некоторые глубоководные моллюски (кальмары, каракатицы).

    Есть и совершенно другие моллюски, способные к свечению. Это так называемые точильщики, проделывающие ходы в мягком камне. Значение свечения для этих моллюсков остается пока неясным. Возможно, в данном случае свет является просто побочным продуктом какой-нибудь жизненно важной реакции.

    Также не ясна роль свечения у бактерий и грибов, среди которых известно довольно много светящихся видов. Именно за счет них светятся гниющие пни. Кстати, светящиеся органы многих глубоководных хищников (рыб и моллюсков) часто тоже работают за счет симбиотических бактерий. Многие бактерии светятся не постоянно, а только если их чем-то потревожить. Аналогичная реакция свойственна и некоторым простейшим, из которых широкой известностью пользуется Ночесветка, относящаяся к динофлагеллятам. Именно эти организмы способны вызывать свечение моря в теплых широтах. Возможно, яркая вспышка света в ответ на прикосновение может являться защитной реакцией, хотя и не совсем ясно, кого может отпугнуть своей вспышкой столь маленькое существо.

    Пожалуй, труднее всего найти примеры свечения у растений. Известен пещерный мох, который слабо светится во мраке, но он не обладает собственным механизмом генерации света, а лишь фокусирует и отражает слабый свет, поступающий снаружи. Некоторые светящиеся растения были созданы человеком в чисто научных целях. Для того, чтобы проверить, как работает система регуляции генов, ученые подсаживали в растение ген люциферазы - пигмента, обусловливающего свечение светляков. Тогда в эксперименте было легко наблюдать, работает ли данный ген. Но это, конечно, приносило пользу ученым, а не самому растению.

  3. Функции клюва весьма разнообразны, что отражается на разнообразии его форм. Клюв служит для схватывания добычи, ее расчленения, для осязания, нападения и защиты, передвижения, для долбления, рытья, зондирования грунта, а также сложных действий, связанных с уходом за оперением, постройкой гнезда и др. В наибольшей степени форма клюва обусловлена характером пищевой специализации птиц.

  4. Регенерация - восстановление организмом утраченных или поврежденных органов и тканей. У разных групп животных регенерация выражена в разной степени. Чем примитивнее животное, тем больше у него возможностей восстановить утраченное. Так у многих низших беспозвоночных (кишечнополостные) возможна регенерация целого организма из небольшого кусочка тела. У низших позвоночных (земноводные) могут восстанавливаться целые конечности, хвост, разные части глаза, внутренние органы и ткани, а у млекопитающих и человека возможна регенерация лишь отдельных тканей.

  5. Млечный сок и смола очень часто встречаются в растительном мире. Несмотря на это во многих случаях функция их в растении остается неясной. Поэтому при оценке ответа на данный вопрос любое разумное предположение оценивалось положительно.

    Чаще всего млечный сок и смола играют защитную роль. Наличие "невкусного" или ядовитого млечного сока может довольно эффективно защищать растение от поедания различными животными. С другой стороны, многие смола обладают бактерицидным действием и защищают растение от проникновения инфекции, особенно через раны. Некоторые смолы кроме того могут ускорять процесс заживления раны, стимулируя рост окружающих тканей.

    В ряде случаев, когда млечный сок или смола выводятся растением из организма, вместе с ними могут выводится и ненужные и даже вредные для растения вещества.

    Человек довольно широко использует смолы и млечный сок растений для разных целей. Вот некоторые примеры:

    В промышленности смолы используются для производства лаков, красок, мастик, смазочных масел, растворителей (скипидар) и т.п. Все эти продукты широко используются в быту.

    Из млечного сока растений получают каучук и гуттаперчу. Правда, в наше время аналогичные материалы в основном получают путем химического синтеза, однако для некоторых специальных целей использование натуральных продуктов предпочтительно.

    В медицине могут применятся продукты переработки смол, в частности, всем известная камфара.

    Кроме того, из смол получают канадский бальзам и иммерсионные масла, необходимые для микроскопии; канифоль, которая широко используется музыкантами, спортсменами и радиотехниками; сургуч; ароматические масла и смолы (в частности, ладан). Перечислить все области применения смол практически невозможно.

    Некоторые школьники упоминали в своих ответах янтарь, употребляемый для изготовления ювелирных изделий. Если при этом упоминалось, что янтарь является окаменевшей смолой ископаемых растений, такой ответ тоже засчитывался как правильный.

  6. Биологические методы изучения чистоты водоемов основаны на том, что водные организмы и бентосные - обитающие на дне, и планктонные - парящие в толще воды, и перифитонные - обрастатели чутко относятся к качеству воды, в которой они обитают. Одни организмы могут жить только в очень чистой воде, другие предпочитают некоторую степень загрязнения, третьи же отлично чувствуют себя в сильно загрязненных водах. Требования к чистоте воды известны для многих организмов, они могут служить индикаторами чистоты воды. Изучив видовое разнообразие, мы без труда определим чистоту водоема. Систематический анализ - соотношение таксонов, к которым относятся обитатели водоема также имеет индикаторную ценность.

    Сообщества каждой из групп не случайны. Организмы, обитающие в чистых водах, не бывают многочисленными. Немного, но разнообразно - девиз чистых водоемов; в загрязненных водоемах разнообразие сохраняется, но появляются доминирующие - массово представленные виды; Водоемы с грязной водой заселены небольшим числом видов, количество же и биомасса выдерживающих загрязнение видов могут быть поистине огромными. Изучение структуры сообщества, как мы видим, может многое сказать о чистоте водоема.

    И наконец о чистоте водоема свидетельствует и скорость заселения чистых субстратов. Новые поверхности в чистых водоемах заселяются медленно, в грязных - быстрее; следя за скоростью смены сообществ, мы можем определить качество воды.

  7. В работах школьников часто говорилось, что математика в биологии применяется для измерений различного рода, но ведь процесс измерения нельзя назвать математическим методом. Математическим методом является статистическая обработка любых количественных результатов, например тех же промеров. Статистическая обработка результатов используется абсолютно во всех отраслях биологии: в зоологии, ботанике, биохимии, физиологии, экологии и т.д. Особенно тесно оказалась связанной с математической статистикой генетика, закономерности которой выявляются только в больших выборках.

    Используется в биологии и математическое моделирование. На любой, даже самый простой биологический процесс, как правило, влияет такое большое количество факторов, что выявить закономерности почти невозможно, вот и приходится моделировать ситуации, в которых факторы действуют не все вместе. Этот метод широко применяется в экологии и эволюционном учении, для изучения популяций, эмбриологии и т.д.

  8. И у мужчин, и у женщин одинаковое количество ребер - двенадцать пар (24 ребра).

  9. Хотя в любом учебнике можно найти сходные определения для продуцентов, редуцентов и консументов, но на практике понять какой организм к какой группе должен быть отнесен не всегда легко. Ведь любой живой организм и растительный, и животный, и крошечная бактерия использует органические вещества для своего обмена, а в результате энергетического обмена (дыхания) выделяет минеральные вещества - углекислый газ и воду. Так что попробуй проведи четкую границу между консументами и редуцентами! В свою очередь, высшие растения, имеющие большое количество клеток, неспособных к фотосинтезу и питающихся как гетеротрофы, также могут вызвать сомнения. Поэтому при оценке работ учащихся отдельно учитывалась попытка определить границы групп. Если пользоваться определениями, данными в вопросе, и считать, что консументы - крупные организмы, редуценты же - микроконсументы - грибы и бактерии, то можно организмами, являющимися одновременно продуцентами и консументами считать насекомоядные растения; граница между редуцентами и консументами условна, поэтому одновременно редуцентом и консументом: редуцентом, консументом и продуцентом организм быть не может, а вот консументом и продуцентом можно считать миксотрофных простейших, например, эвглену зеленую, способную питаться и автотрофно, и сапротрофно. Если же рассматривать устойчивые симбиозы, то возможно найти примеры для каждой группы.

  10. Полимеры компактнее - занимают меньше места; полимеры химически инертны, хуже растворимы - это облегчает их хранение и предохраняет от единовременного использования всей глюкозы. Но самое главное, большое количество мелких, хорошо растворимых молекул влияет на физико-химическое состояние цитоплазмы, резко изменяет осмотическое состояние клетки. Вспомните плазмолиз - сжатие или набухание клетки в зависимости от соотношения количества соли вне и внутри клетки. Клетка с большим количеством растворенных в цитоплазме молекул будет активно вводить молекулы воды, до уравнивания концентраций молекул. Это может привести к тому, что клетка лопнет. Но даже если этого не произойдет, изменение физико-химического отрицательно скажется на нормальном протекании клеточных процессов. Как известно, осмотическая сила раствора определяется числом молекул растворенного вещества в определенном объёме раствора. Поэтому, если мелкие молекулы (например, глюкозы) объединить в одну крупную молекулу полимера, осмотическая сила раствора будет значительно меньше и клетка сможет хранить запасные вещества, не подвергаясь опасности насасывания лишней воды.

    Полимеры могут быть использованы для выполнения особых функций - целлюлоза образует клеточную стенку растительной клетки.

Конкурс по лингвистике

Задачи

  1. (автор И. Б. Иткин) Даны русские личные имена и образованные от них фамилии и женские отчества:

    Илья - Ильин - Ильинична
    Иона - Ионов - Ионовна
    Кирилл - Кириллов - Кирилловна
    Кузьма - Кузьмин - Кузьминична
    Леонид - Леонидов - Леонидовна
    Лука - Лукин - Лукинична
    Никита - Никитин - Никитична
    Роман - Романов - Романовна
    Савва - Саввин - Саввична
    Фёдор - Фёдоров - Фёдоровна
    Фока - Фокин - Фокична
    Фома - Фомин - Фоминична

    От одного из имен фамилия и отчество образованы неправильно, хотя и считаются нормативными.
    А. Найдите это имя.
    Б. Какие правила образования русских фамилий и женских отчеств Вы можете сформулировать на материале задачи?

  2. (автор М. С. Гельфанд) Даны числительные татского языка: 
                v  v
 26 - bisti saes        

 67 - sae bisti hae ft
      v             ..
 92 - carbistdae h dy
       ..                  ..
279 - dy sad sae bistdaeh nyh
                   v
314 - sae sad dae hcar

    Запишите по-татски: 16, 83, 327, 999. 

                     ..                   v  v
Примечание. ae , y - особые гласные, c, s -
особые согласные татского языка.

    Татский язык относится к иранской группе индоевропейской семьи языков. На нем говорит более 15 тысяч человек в Азербайджане, Дагестане, Ингушетии, Кабардино-Балкарии, Северной Осетии и Чечне.

    Замечание по оформлению. Т.к. стандартными средствами HTML невозможно отобразить некоторые использованные в задаче символы, они обозначены следующим образом: стоящие подряд две буквы ae обозначают один символ, получающийся совмещением вертикальной линии, расположенной с правой стороны a с вертикальной линией, расположенной с левой стороны e, знаки v и .. на одну строку выше основного текста означают соответствующие диакритические знаки над расположенными под ними буквами.

  3. (автор М. Е. Алексеев) Даны словосочетания на цезском языке и их переводы на русский язык в перепутанном порядке:

    ъIонес хаза, ужис хаза, ужис шуша, ъIонес махIи, бекъес махIи, ужис гьутI, шушарес гьутI

    бутылка мальчика, рот мальчика, пятка мальчика, обух топора, топорище, хвост овцы, горлышко бутылки

    Установите правильный перевод каждого цезского слова.

    Примечание. ъI, хI, тI, гь, къ - особые согласные звуки цезского языка.

    Цезский язык - один из бесписьменных дагестанских языков, на котором говорит около 7 тыс. человек.

Решения задач конкурса по лингвистике

  1. Как видно из условия, все представленные в задаче фамилии оканчиваются либо на -ов (Кириллов), либо на -ин (Кузьмин), а отчества - либо на -овна (Леонидовна), либо на -ична (Саввична), либо на -инична (Ильинична). При этом если фамилия оканчивается на -ов, то соответствующее ей отчество всегда оканчивается на -овна и наоборот, а если фамилия оканчивается на -ин, то отчество может оканчиваться как на -ична, так и на -инична.

    Таким образом, нам необходимо установить, какими факторами определяется выбор показателей -ов и -ин в фамилиях, а также -овна, -ична или -инична в женских отчествах. Чтобы сделать это, представим весь имеющийся в задаче материал в виде следующей таблицы:
    Фамилии на -ов на -ин
    Отчествана -овнана -ичнана -инична
    Имена Иона Никита Илья
    Кирилл Савва Кузьма
    Леонид Фока Лука
    Роман Фома
    Фёдор

    Сразу бросается в глаза, что фамилии на -ов (и, соответственно, отчества на -овна) образуются от имен II склонения (типа Роман, Фёдор), а фамилии на -ин и отчества на -ична и -инична - от имен I склонения (типа Никита, Кузьма). Единственное имя, нарушающее данную закономерность, - это имя Иона; очевидно, это и есть искомое исключение.

    Значительно сложнее установить, отчего зависит выбор показателей -ична и -инична; между именами, относящимися ко второму и третьему столбцам, нет никаких различий в склонении, не играет роли и характер конечной согласной корня (ср. Фока и Лука). Остается единственное предположение: все дело - в ударении. Действительно, у имен Ники'та, Са'вва, Фо'ка оно падает на корень, а у имен Илья', Кузьма', Лука', Фома' - на окончание, причем первые три имени образуют женские отчества с помощью суффикса -ична, а остальные четыре - с помощью суффикса -инична; следовательно, наше предположение полностью подтвердилось.

  2. Обратившись к первым трем числительным, можно предположить, что первое слово означает число десятков, а второе - число единиц.

    Рассмотрим два последних числительных. Они в татском языке имеют общую часть sad, что, видимо, означает 100. Тогда dy.. - 2, sae - 3. Это предположение согласуется с первым предположением: в третьем числительном dy.. - 2.

    Сравним первые два числительных. svaesv - 6, hae ft - 7. Bisti - 20, sae bisti - 60. Но из последнего примера мы знаем, что sae - это 3. Следовательно, 60 представляется как 3*20. Значит, в татском языке - двадцатиричная система счисления.

    В четвертом числительном видим, что 70 - это sae bistdae h. Сравнив это с записью для 60, понимаем, что 70 представляется как 3*20+10. Отсюда dae h - 10. Причем, если в числительном полное число двадцаток, есть окончание -i (bisti, sae bisti), если прибавляется еще 10, то для записи двадцати используется вариант bist (sae bistdae h).

    В третьем числительном cvarbistdae h переводится как 90 и представляется как 4*20+10, откуда cvar - 4.

    В пятом примере 14 "dae hcvar" представляется как 10 + 4. Еще одно неназванное слово из четвертого примера ny..h - 9.

    Теперь легко выполнить задание: 16 - dae hsvaesv; 83 - cvarbisti sae; 327 - sae sad bisti hae ft; 999 - ny..h sad cvarbistdae h ny..h.

    Примечание: сочетанием символов y.. обозначен символ у с двумя точками сверху (как у буквы ё), sv - символ s с галочкой сверху в центре, аналогично sv; подряд стоящие буквы ae также обозначают один симсвол (см. примечание в конце условия этой задачи).

  3. В цезских словосочетаниях только одно слово повторяется три раза: ужис. В русских переводах три раза повторяется слово мальчик, причем все три раза это слово выступает в роли определения и стоит после определяемого существительного в форме родительного падежа. В цезских словосочетаниях слово ужис стоит на первом месте. Очевидно, что ужис - это мальчик (в роли определения), а порядок слов в цезских словосочетаниях такой: определение + определяемое. Замечаем также, что определения в цезском оканчиваются на -с. В качестве определяемых в рассматриваемых трех цезских словосочетаниях употреблены слова хаза, шуша и гьутI, которым соответствуют (пока неизвестно, в каком порядке) бутылка, рот и пятка.

    Среди цезских словосочетаний находим такое, в котором представлены два слова, уже встреченные нами в роли определяемых со словом ужис ("мальчик"): шушарес гьутI. Из данных русских переводов для этого словосочетания годится только горлышко бутылки. Итак, шуша - бутылка, гьут - рот(мальчика)/горлышко (бутылки). Очевидно, что хаза (третье слово, сочетающееся со словом ужис) - это пятка.

    В трех еще не переведенных цезских словосочетаниях одно слово не повторяется - бекъес. Очевидно, это овца (в роли определения). Тогда махIи - хвост. Это же слово входит в словосочетание ъIонес махIи "хвост топора" - топорище. Оставшееся словосочетание ъIонес хаза переводится как обух ("пятка") топора.

Конкурс по истории

Задачи

  1. Когда жили и чем прославились следующие деятели русской истории?

    Александр Данилович
    Афанасий Лаврентьевич
    Варфоломей Кириллович
    Владимир Всеволодович
    Гавриил Алексеевич
    Григорий Лукьянович
    Мстислав Владимирович
    Павел Степанович
    Петр Аркадьевич
    Федор Васильевич

  2. Перечислите тех полководцев, которые сражались против Суворова. Где и когда, с каким результатом?
  3. Была ли связь между падением Константинополя в 1453 году и открытием Америки?
  4. Какой город Западной Европы более всего похож на Новгород по своей исторической роли? В чем проявилось сходство, каковы его причины?
  5. Перечислите 7 чудес Средневековья, построенных с 300 по 1500 год и сохранившихся до наших дней. (Не более 2 чудес из одной страны!)
  6. Известно, что годовой бюджет Венеции в 14 веке был больше, чем годовой бюджет Франции. Как это можно объяснить?
  7. Перечислите 10 храмов Москвы в порядке их постройки, с указанием их местонахождения и посвящения. (Не более 3 храмов из одного века!)
  8. Составьте распорядок дня одного из фараонов Египта (указав его имя и примерное время правления).
  9. Как вы думаете: была ли Неолитическая революция (или Индустриальная революция) неизбежной? Как вы можете обосновать свое мнение?
  10. Допустим, что в 13 веке монголы не дошли до Руси. Составьте вероятный сценарий дальнейшей русской истории на 200 лет или на больший срок.
  11. Перечислите европейских ученых - современников Мартина Лютера. Какие открытия они сделали?
  12. Придумайте возможную биографию английского рыцаря Питера, который погиб в 1242 году, сражаясь в рядах армии Батыя. С кем из своих знаменитых современников он мог встречаться, в каких событиях участвовать?
  13. Найдите в тексте исторические ошибки.

ТРИУМФ (текст с ошибками)

Первый день 800 года от Основания Города был праздничным. В этот день, по обычаю, приносили присягу на верность Республике новые консулы и трибуны, а сенат наказывал им: "Будьте бдительны, чтобы народ не понес никакого ущерба". Распорядитель праздника - император Марк Калигула, потеряв реальную власть в результате заговора сенаторов, сохранил лишь стойкие симпатии плебеев да почетный титул - Магистер Милитум - командующий конницей, которая со времен Цезаря стала ведущим родом войск в римской армии. В ней служили полноправные римские граждане, а пехоту вербовали из италиков и прочих варваров: готов, галлов, сарматов, даков и лангобардов.

В первый день Нового Года эта армия совершала триумфальный марш по улицам Вечного Города во главе с Диктатором - полководцем, наиболее отличившимся в истекшем году. На этот раз высшая почесть выпала Юлию Северу - недавнему покорителю Британии, только что подавившему мятеж Бар-Кохбы в Иудее. Хорошо, что эта операция прошла так быстро - прежде чем вмешались персы, извечные враги Рима!

Этих варваров пора, наконец, укротить - таково общенародное мнение. Иудея больше не восстанет - ведь Иерусалим разрушен, а на его месте строится новый римский город, Элия Капитолина. Заселят его, по обычаю, римские ветераны и местные христиане: эта новая секта оказала большие услуги римлянам в борьбе с Бар-Кохбой, так что сенат объявил христиан "Союзниками римского народа". Большая делегация христиан участвует в нынешнем триумфе; римляне с любопытством глядят на странных безбородых людей, одетых в длинные хитоны и повесивших себе на грудь большие деревянные кресты.

Впрочем, римлянам доводилось видеть в Городе и более странных союзников: чернокожих нумидийцев Югурты, татуированных бриттов Ариовиста, размалеванных и одетых в кожаные штаны даков Децебала. Интересно, как будут выглядеть пленные персы в следующей триумфальной процессии? Жаль, что их не успел покорить сто лет назад великий Цезарь, убитый презренными заговорщиками! Но теперь выросли его преемники - и римский народ не позволит вновь лишить себя своих лучших вождей! Вот они идут вслед за колесницей Юлия Севера: Луций Эмилий Павел, Марк Ульпий Траян, Публий Игнатий Галлиен. Кого из них Немезида выберет для завершения великих дел Суллы на Востоке? Это решит жребий: так повелось в Риме с той поры, когда Цезарь впервые узнал волю Судьбы, бросив жребий на берегу Рубикона с вопросом: помириться ли с Помпеем, или объявить ему войну?

Тогда Немезида решила судьбу Рима; теперь она решит судьбу Ирана и тех земель Востока, по которым со времен Александра Великого не ступала нога европейца. Многие народы этих земель готовы сбросить персидское иго, если Рим поможет им. Недавно в Городе побывало тайное посольство из Индии с просьбой об избавлении от ига огнепоклонников. Значит, час настал: скоро волчьи головы на хоругвях легионов перешагнут Евфрат и Яксарт, достигнут Инда и Ганга. Индийский океан наполнится римскими судами; эти воды тоже назовут "Нашим морем" , как давно называют Понт Евксинский, вырванный римлянами из рук этрусков и египтян.

А что ждет Вечный город дальше? Сенат и народ Рима не думают об этом. Только Верховный жрец Клавдий (брат юного императора) заинтересовался сообщениями послов неведомого варварского народа - гуннов, впервые прибывших в Рим. Эти жители степей к северу от Понта просят у римлян защиты от своих восточных врагов - скифов, которых поддерживает далекое восточное царство Сун, каждый год присылающее в Рим караваны с драгоценным шелком. Сколько золота уплыло уже на Восток в обмен на эти ткани! Казна Республики пустеет; этому пора положить конец! Вот новое дело для конных армий Юлия Севера: как только Иран и Индия подчинятся римскому оружию, станет возможно навести порядок в Степи и покорить страну Сун. Тогда потомки Ромула и Волчицы превзойдут славой великого Александра, а весь населенный мир будет жить по законам 12 таблиц - как завещал Цезарь сто лет назад ...

Такие мысли занимали умы просвещенных римлян в их последнем юбилейном году. Никто не подозревал, что через считанные годы чума опустошит Республику; ее законы рухнут, сменившись произволом Гражданской войны, из которой вырастет новая Империя - с христианством в роли государственной религии.

Решения задач конкурса по истории



  1. Когда жили и чем прославились следующие деятели русской истории? (список имён и отчеств)
    Александр Данилович Меншиков (соратник Петра 1);
    Афанасий Лаврентьевич Ордин-Нащокин (дипломат, первый министр Алексея Михайловича);
    Варфоломей (Сергий) Кириллович Радонежский;
    Владимир Всеволодович Мономах;
    Гаврила Олексич (дружинник и боярин Александра Невского, герой Ледового побоища);
    Гавриил Алексеевич Малюта Скуратов-Бельский (сподвижник Ивана Грозного);
    Мстислав Владимирович Великий (сын и преемник Владимира Мономаха), либо
    Мстислав Владимирович Тмутороканский (брат и соперник Ярослава Мудрого, "иже зареза Редедю пред полки касожскими");
    Павел Степанович Нахимов - адмирал;
    Петр Аркадьевич Столыпин - министр (автор земельной реформы 1900-х годов);
    Федор Васильевич Курицын - дьяк (министр иностранных дел при Иване 3).

  2. Перечислите тех полководцев, которые сражались против Суворова. Где и когда, с каким результатом?
    Турецкие полководцы:
    Осман-паша (при Фокшанах),
    Юсуф-паша(при Рымнике),
    Айдзоли Мехмет-паша (комендант Измаила);
    польский лидер
    Тадеуш Костюшко;
    русский мятежник
    Емельян Пугачев (взят в плен Суворовым);
    Генералы Французской республики:
    Жубер (погиб при Нови),
    Макдональд (разбит при Требии),
    Моро и
    Массена (единственный победитель Суворова: он отразил его наступление на Цюрих, окружил корпус Римского-Корсакова и вынудил Суворова отступать через Альпы).

  3. Была ли связь между падением Константинополя в 1453 году и открытием Америки?
    Взятие турками Константинополя положило конец самовластью венецианских и генуэзских купцов в Причерноморье - в западном конце Шелкового пути. Высокие таможенные пошлины для христиан, установленные Османами, вынудили западных европейцев настойчиво искать иные пути в Индию - вокруг турецких владений. При этом Колумб открыл Америку.

  4. Какой город Западной Европы более всего похож на Новгород по своей исторической роли? В чем проявилось сходство, каковы его причины?
    Ближе всего к Новгороду города-республики Северной Италии - Флоренция, Венеция и Генуя - и сходные с ними города Ганзейского союза в Германии и Нидерландах (Любек, Бремен, Брюгге, Антверпен).

  5. Перечислите 10 храмов Москвы в порядке их постройки, с указанием их местонахождения и посвящения. (Не более 3 храмов из одного века!)
    Собор Святой Софии в Константинополе (6 век),
    храм Кааба в Мекке (7 век),
    буддийский холм-храм Боробудур на Яве (8 век),
    майянский город Ушмаль в Мексике (9 век),
    Вестминстерское аббатство в Англии (11 век),
    храм Покрова на Нерли (12 век),
    Амьенский собор во Франции (13 век),
    статуи острова Пасхи и
    мавзолей Гур-Эмир в Самарканде (14век),
    Московский Кремль и
    дворец Гугун в Пекине (15 век).

  6. Известно, что годовой бюджет Венеции в 14 веке был больше, чем годовой бюджет Франции. Как это можно объяснить?
    Экономика Венеции в 14 веке имела уже денежную основу: главной частью государственных доходов были пошлины с заморской торговли. Во Франции преобладала натуральная экономика: феодалы-землевладельцы не платили денежных налогов, а несли бесплатную службу в войсках и в администрации. Денежные доходы короля Франции поступали из его личных поместий и из немногочисленных "вольных" городов - но те и другие были разорены Столетней войной. Венеция в 14 веке почти не воевала, и потому была (в денежном выражении) богаче Франции.

  7. Перечислите 10 храмов Москвы в порядке их постройки, с указанием их местонахождения и посвящения. (Не более 3 храмов из одного века!)
    Спасский собор Андроникова монастыря (начало 15 века),
    Успенский собор в Кремле (конец 15 века),
    Архангельский собор в Кремле и
    храм Вознесения в Коломенском (начало 16 века),
    Покровский собор на Красной площади (середина 16 века),
    храмы Покрова в Филях и
    Троицы в Никитниках (17 век),
    "Меншикова башня" на Антиохийском подворье (18 век),
    храм Большого Вознесения у Никитских ворот (начало 19 века),
    храм Христа Спасителя у Москвы-реки (конец 19 века).

  8. Составьте распорядок дня одного из фараонов Египта (указав его имя и примерное время правления).
    Ответ на этот вопрос мы не приводим, т.к. ответ на этот вопрос потребовал бы написание историко-литературного эссе.

  9. Как вы думаете: была ли Неолитическая революция (или Индустриальная революция) неизбежной? Как вы можете обосновать свое мнение?
    Обе эти революции можно считать неизбежными - как и все крупные изменения в стихийной эволюции человечества (возникновение рабства и феодализма, изобретение мореплавания, книгопечатания и т.п.). Доказательством этой гипотезы может служить тот факт, что многие народы в разных концах Земли проходили эти фазы независимо - а начавшись в одной точке, они быстро охватывали большинство человечества.

  10. Допустим, что в 13 веке монголы не дошли до Руси. Составьте вероятный сценарий дальнейшей русской истории на 200 лет или на больший срок.
    Ответ на этот вопрос мы не приводим по тем же причинам, что и на задачу 8.

  11. Перечислите европейских ученых - современников Мартина Лютера. Какие открытия они сделали? Гуманисты - Томас Мор в Англии и Эразм Роттердамский в Голландии; историк Никколо Макиавелли во Флоренции; врачи Андрей Везалий в Голландии (автор анатомического атласа) и испанец Мигель Сервет (открыватель малого круга кровообращения); астроном Николай Коперник в Италии и Польше; универсальный естествоиспытатель Леонардо да Винчи (автор первых проектов вертолета, телевизора и водолазного колокола).

  12. Придумайте возможную биографию английского рыцаря Питера, который погиб в 1242 году, сражаясь в рядах армии Батыя. С кем из своих знаменитых современников он мог встречаться, в каких событиях участвовать?
    Питер мог быть рыцарем-тамплиером, который, пытаясь проникнуть из Палестины в Среднюю Азию, встретил наступающую армию монголов и подружился с ними (поскольку они были врагами мусульман, а к христианам относились терпимо). В войске Батыя Питер, видимо, командовал разведкой. Он попал в плен к католикам после поражения монголов при Оломоуце в Чехии и, видимо, был казнен как "изменник". Сообщение о Питере сохранилось в архиве Ватикана - в донесении папского легата.

Комментарии к ошибкам в тексте "Триумф"

  1. 800 год от основания Рима - это 47 год н.э. В это время Римская держава фактически превратилась в Империю, хотя официально она еще именовалась Республикой. Поэтому сенат регулярно заседал и ежегодно избирал консулов. Но кандидатов в консулы предлагал император; он контролировал все решения сената и обычно присваивал себе также права народного трибуна (включая личную неприкосновенность).
  2. В 47 году императором был Клавдий. Его племянник (предыдущий император) Гай Калигула погиб в 41 году в результате заговора офицеров гвардии, к которому сенаторы не имели отношения.
  3. Калигула был очень популярен в юности - но став императором (в 37 году), он сделался таким тираном, что заслужил общую ненависть римлян.
  4. В формулировке присяги консулов и иных магистратов "народ" не упоминался - они присягали Республике.
  5. Сам император никогда не бывал распорядителем триумфа; обычно эту работу исполнял один из консулов.
  6. В имперскую эпоху право на триумф принадлежало только императорам. Они также присвоили себе титул главнокомандующего всей армией - Магистер Милитум.
  7. Во времена Республики право на триумф сенат даровал полководцам, одержавшим самые громкие победы в истекшем году. Такие полководцы получали почетный титул "император" ; во время триумфа им воздавали божеские почести.
  8. Конница считалась в римской армии (до 4 века н.э.) вторым по значению родом войск. Ее командир - Магистер Эквитум - был заместителем главнокомандующего.
  9. Римская пехота набиралась из граждан, а в коннице обычно служили союзники ("федераты" ) - в том числе "варвары" (германцы, мавры).
  10. Со времен объединения Италии в 3 веке до н.э. римляне не называли италиков варварами. Галлы в середине 1 века (через 100 лет после их покорения Цезарем) уже не считались варварами; многие из них служили в легионах.
  11. Готы появились возле римских границ только в конце 2 века.
  12. Лангобарды стали известны римлянам только в 5 веке - во время Переселения народов.
  13. Титул "Диктатор" получал от сената на короткий срок (не более полугода) единовластный правитель Римской республики, заменявший обоих консулов и командовавший всей армией. После Цезаря никто из римских императоров не принимал этот титул.
  14. Полководец Юлий Север был наместником Британии при императоре Адриане в 120-х годах. Он продвинул границу римских владений на север - до Шотландии. После этого Адриан поручил Юлию Северу подавить восстание Симона Бар-Кохбы в Иудее (133-135 годы). Юлий Север не связан родством с императорской династией Северов, которую основал в 190-е годы Септимий Север.
  15. В первые века н.э. главными врагами Рима на востоке и владыками Ирана были не персы, а родственный им народ - парфяне. Они создали свое царство в 250 году до н.э., разбили войско Красса в 53 году до н.э., были побеждены Траяном в 117 году и готовились помочь Бар-Кохбе в 133 году. В 226 году восставшие персы уничтожили Парфию и возобновили войну с Римской империей.
  16. После первого восстания в Иудее (66-70 годы) римляне разрушили храм в Иерусалиме и стены этого города - но сам город уцелел. После второго восстания Бар-Кохбы Иерусалим был полностью разрушен; иудеям было запрещено селиться на этом месте, и римляне построили там свой город, названный Элия Капитолина (в честь императора - Элия Адриана).
  17. В 40-е годы маленькая секта христиан существовала только в Иудее. Римляне узнали о ней только в 60-е годы, когда первые христианские проповедники (в их числе - Петр и Павел) проникли в Рим.
  18. В 1 веке н.э. христиане подвергались гонениям как со стороны римских властей, так и со стороны правоверных иудеев. Поэтому они не участвовали в иудейских восстаниях, но и не помогали римлянам их подавлять. Христиан (как и иудеев) никогда не награждали титулом "союзники римского народа" , и в римских триумфах они не участвовали (разве что в качестве пленников).
  19. Внешне христиане ничем не отличались от прочих подданных римской державы; небольшие кресты они носили под одеждой.
  20. Хитон - греческая (а не иудейская) одежда. Бритое лицо в 1 веке н.э. характерно для коренного римлянина - иудеи и христиане обычно носили бороды.
  21. Царь Югурта был врагом римлян во 2 веке до н.э.; он был побежден Марием и казнен после его триумфа. Позднее другие нумидийские цари были вассалами Римской державы - но в Рим их войска не входили.
  22. Ариовист был вождем германцев (а не бриттов) и противником Цезаря в середине 1 века до н.э. Он был побежден и погиб - но в плен не попал и в триумфах Цезаря не участвовал.
  23. Децебал был вождем даков в начале 2 века и возглавил их войну против Рима. Побежденный Траяном, Децебал покончил с собой.
  24. В 1 веке кожаные штаны были обычной одеждой любых конников - в том числе римских солдат.
  25. Цезарь в последние месяцы своей жизни готовился к походу на Парфию, но не успел его начать.
  26. Луций Эмилий Павел - имя нескольких римских полководцев 3-2 веков до н.э.: один из них погиб при Каннах, другой разгромил македонцев при Пидне.
  27. Марк Ульпий Траян (император в 98-118 годах) в 47 году еще не родился.
  28. Публий Лициний Игнатий Галлиен был императором в конце 3 века.
  29. Немезида - греческая богиня, и не судьбы, а возмездия.
  30. Завоевания Суллы на Востоке завершил его помощник Гней Помпей в 60-е годы до н.э. Войска Помпея дошли тогда до Каспийского моря, побывали в Иерусалиме и Египте.
  31. На берегу Рубикона Цезарь не бросал жребий, а лишь произнес слова "Жребий брошен!" Война против сената и Помпея была тогда необходима Цезарю, чтобы сохранить свою власть и жизнь.
  32. Ближний и Средний Восток в 47 году не находился под чьим-либо игом: было равновесие сил двух великих держав - Парфии и Рима.
  33. Индия никогда не была подвластна ни персам, ни парфянам.
  34. Парфяне (в отличие от персов) не поклонялись священному огню. У них были свои боги (дэвы), они также почитали многих греческих богов и Будду.
  35. Хоругви - это христианские знамена, они появились только в 4 веке.
  36. На знаменах легионов были изображены орлиные, а не волчьи головы.
  37. Яксарт - это Сыр-Дарья, она не преграждает римлянам путь в Индию. Им надо пересечь Евфрат и Тигр.
  38. "Нашим морем" римляне называли только Средиземное море - но не Черное море (Понт Евксинский).
  39. Ни этруски, ни египтяне в Черное море не плавали.
  40. Египетское господство над восточной частью Средиземного моря закончилось с приходом персов в 6 веке до н.э. - задолго до выхода римлян на мировую арену.
  41. Этрусское могущество на морях вокруг Италии сокрушили не римляне, а греки (сицилийцы) и финикийцы (карфагеняне) в 5 веке до н.э.
  42. Гунны стали известны римлянам только в середине 4 века, когда они вторглись в Закавказье.
  43. Скифы исчезли как народ в 3 веке до н.э., побежденные сарматами. Таким образом, скифы и гунны никогда не встречались между собой.
  44. В 1 веке жители Средиземноморья называли Китай не "Сун" , а "Син" или "Сер" . Династия Сун появилась только в 10 веке.
  45. Римские войска никогда не вторгались в евразийскую Степь, и тем более не помышляли о подчинении Китая. Даже Иран им не удалось подчинить, хотя Траян однажды захватил парфянскую столицу на Тигре.
  46. Согласно преданию, волчица вскормила Рема и Ромула. Римляне называли себя "потомками Ромула" - но не "потомками волчицы" .
  47. Законы 12 таблиц - это первые римские законы, составленные в 5 веке до н.э. и устаревшие задолго до Цезаря.
  48. Последним юбилейным годом Рима был не 800, а 1200 год - то есть, 447 год н.э. Вскоре после этого Рим был разорен вандаламии и утратил роль столицы.
  49. В первые века н.э. гражданские войны в Риме стали обычным делом. Через 20 лет после 47 года вспыхнула очередная война, связанная со свержением Нерона. Христианство сделалось государственной религией Рима только в 381 году - после новой серии гражданских войн, из которых победителем вышел Феодосий 1.