1. (А. Шаповалов) Тришка отрезал от кафтана квадратный кусок, разрезал его на девять треугольных заплат и сложил их в три кучки по три заплаты. Могло ли оказаться так, что любые две заплаты из одной кучки равны друг другу, а из разных кучек - не равны?
2. (А. Шаповалов) Все целые числа от 1 до 2000 записали в следующем порядке: сперва записали в порядке возрастания все числа, сумма цифр которых равна 1. Затем - все числа с суммой цифр 2 (также в порядке возрастания), потом - все числа с суммой цифр 3 (также в порядке возрастания) и т.д. На каком месте оказалось число 1997?
3. (А. Шаповалов) Сложим все числа, которые получаются из некоторого натурального числа вычеркиванием какой-либо его цифры (слагаемых будет столько, сколько цифр в этом числе). Может ли полученная сумма оказаться равной 1997?
4. (А. Шаповалов) Прямоугольный параллелепипед 1*1*2 перекатывают (через ребра) по клетчатой доске 19*97. Можно ли прокатить его так, чтобы каждую клетку доски параллелепипед покрыл ровно один раз?
5. (Р. Садыков, А. Шаповалов) На доске 4*4 расставляются шестнадцать шахматных коней четырех мастей - четыре вороных, четыре соловых, четыре гнедых и четыре каурых. Существует ли такая расстановка коней, в которой вороные не бьют соловых, соловые - гнедых, гнедые - каурых, а каурые - вороных?
6. (А. Шаповалов) Найдутся ли три таких различных положительных числа a, b и c, что уравнения ax+b=c и x/a+1/b=1/c имеют общий корень?
7. (Р. Женодаров) В выпуклом пятиугольнике ABCDE сторона AB равна стороне AE, а сторона BC равна стороне DE, точка F - середина отрезка CD. Докажите, что если AF | CD, то точка пересечения прямых BD и CE лежит на прямой AF.
8. (А. Шаповалов) Каждая из 55 участниц женского собрания написала, у скольких из присутствующих возраст (число полных лет) не совпадает с ее возрастом. К их ужасу оказалось, что каждая написала именно свой возраст в годах! Каково наибольшее количество различных чисел могло быть среди написанных возрастов?
9. (А. Шаповалов) Можно ли разрезать квадрат на конечное число равнобедренных треугольников с углами 75o при основаниях?
10. (Р. Женодаров) Существует ли такое натуральное число n, что для любой пары нечетных цифр a и b число вида a00...0b (между a и b - ровно n нулей) делится нацело на 10a + b?
11. (С. Волченков) Дана окружность K1 с центром O и диаметром AB. На отрезке OA, как на диаметре, построена окружность K2. Из точки O под углом 45o к OA проведен луч, пересекающий K2 в точке C (C не равно O), а K1 - в точке D. Докажите, что фигура ACD, ограниченная отрезками AC и CD и меньшей из двух дуг AD, делится окружностью K2 на две части равной площади.
12. (А. Шаповалов) Жесткий квадратный проволочный контур со
стороной 1 см разрезали на части, после чего некоторые части переложили и
спаяли новый плоский замкнутый несамопересекающийся контур.
а) Были сделаны разрезы ровно в трех точках контура. Какую наибольшую
площадь может охватывать новый контур?
б) Были сделаны разрезы ровно в четырех точках контура. Могла ли площадь,
охватываемая контуром, увеличиться?
13. (А. Шаповалов) Найдите наибольшее натуральное число, у которого сумма и произведение цифр такие же, как и у числа 1997.
14. (А. Шаповалов) Пьяный шахматный король стоит в центре доски 5*5. Может ли он побывать на каждом поле, кроме исходного, ровно по одному разу и последним ходом вернуться на исходное поле, если делать два хода подряд в одном и том же направлении он не в состоянии?
15. (Р. Женодаров) На плоскости проведено семь прямых, из которых любые две пересекаются и никакие три не проходят через одну точку. Когда плоскость разрезали по этим прямым, среди полученных частей оказалось ровно семь углов (угол - это часть плоскости, ограниченная двумя лучами с общей вершиной). Найдите сумму величин этих углов.
16. (Р. Садыков) На доске 1*17 слева выставлены восемь белых фишек, справа - восемь черных, среднее поле свободно. Два игрока ходят по очереди, каждый - фишками своего цвета (начинают игру, естественно, белые). За ход игрок переставляет любую свою фишку на свободное поле: белую - вправо, а черную - влево. Выигрывает тот игрок, кто первым переставит все свои фишки на сторону противника или лишит противника возможности сделать очередной ход. Кто из игроков может выиграть, независимо от игры соперника?
17. (Максим Шаповалов) Красящий хамелеон - сказочная шахматная
фигура, которая с любого поля ходит на соседнее по вертикали или горизонтали
поле. При этом, попадая на некоторое поле, хамелеон либо красит это поле в свой
цвет, либо перекрашивает себя в цвет этого поля. На черно-белой шахматной доске
перекрасили все черные поля в белый цвет, а затем поставили туда черного
хамелеона.
а) Докажите, что он не сможет добиться полного восстановления
первоначальных (до перекрашивания) цветов полей.
б) Всякую ли раскраску доски в белый и черный
цвета можно получить с его помощью?
в) Через несколько ходов хамелеона оказалось, что ровно N полей
покрашены в свой первоначальный (до перекрашивания) цвет. Найдите наибольшее
возможное значение N.
18. (А. Шаповалов) На доске выписали девять чисел - длины биссектрис, высот и медиан некоторого треугольника. Оказалось, что среди этих чисел не более трех различных. Докажите, что рассматриваемый треугольник - равносторонний.
19. (Р. Женодаров, О. Крижановский) Назовем натуральное число n хорошим, если набор чисел 1, 2, 3, ..., 2n можно разбить на пары, сумма чисел в каждой из которых есть степень двойки. Найдите все хорошие числа.
20. (А. Штерн)
а) На контурную карту нанесены десять городов (без названий) и железные
дороги между некоторыми из них. Васе задали нанести на карту названия городов.
Он расположения городов не помнил, но смог раздобыть список пар городов,
напрямую соединенных железной дорогой. По его словам, этого хватило, чтобы
однозначно установить название каждого города. Могут ли слова Васи быть правдой?
б) На контурную карту нанесены несколько городов (без названий) и железные
дороги между некоторыми из них. Васе задали нанести на карту названия городов.
Он расположения городов не помнил, но смог раздобыть список пар городов,
напрямую соединенных железной дорогой. Этого Васе вполне хватило, чтобы
однозначно установить название каждого города. Найдите наименьшее возможное
количество городов, нанесенных на контурную карту.
21. (А. Шаповалов) Назовем два натуральных числа двойниками, если суммы их цифр равны друг другу и произведения их цифр также равны друг другу (например, 124 и 2212 - двойники). Найдите все числа, у которых нет двойников.
22. (Р. Женодаров)
а) Пусть x и y - натуральные числа, такие, что
x + y - простое число и
x2 + y2 делится на x + y.
Найдите все такие числа x и y.
б) Пусть x и y - натуральные числа, такие, что
x + y - простое число и
x4 + y4 делится на x + y.
Найдите все такие числа x и y.
23. (А. Шаповалов) Двое играющих по очереди проводят на
плоскости несовпадающие красные или синие прямые (цвет каждый выбирает
независимо от предыдущих ходов), никакие три из которых не должны проходить
через одну точку. После того, как они проведут по 10 прямых, первый игрок
подсчитывает количество точек, в которых пересекаются прямые разных цветов, а
второй - количество точек, в которых пересекаются прямые одного цвета.
Выигрывает тот, у кого окажется больше точек.
а) Докажите, что второй игрок может выиграть независимо от игры первого.
б) Может ли один из игроков выиграть независимо от игры другого, если
каждый из игроков провел не по 10, а по 20 прямых?
24. (О. Крижановский) От картонного треугольника прямолинейным разрезом отделили меньший треугольник, а оставшийся четырехугольник разрезали по диагоналям. Пусть N - наибольшее количество треугольников (из пяти получившихся), имеющих одинаковые наборы углов. Найдите наибольшее возможное значение N.
25. (А. Шаповалов) Разрежьте квадрат со стороной 8 см на восемь многоугольников, для каждого из которых отношение его площади к периметру равно 0,5 см.
26. (А. Шаповалов) На доске выписаны все целые числа от 1 до двузначного числа n. Петя посчитал количество выписанных цифр, и оказалось, что оно записывается теми же цифрами, что и n, но в обратном порядке. Найдите все возможные значения n.
27. (Р. Женодаров) На клетчатой доске 100*100 закрасили n прямоугольников, составленных из двух клеток каждый. Оказалось, что в каждой строке и в каждом столбце есть хотя бы одна закрашенная клетка. При каком наименьшем n это возможно?
28. (И. Рубанов) Петя перегнул квадратный лист бумаги по
прямой линии, получившуюся фигуру снова перегнул по прямой линии, и так
k раз подряд. Затем он в трех местах проткнул согнутый лист шилом,
причем ни один из проколов не пришелся ни на одну из линий сгиба или на край.
Развернув после этого лист, Петя насчитал в нем ровно
а) 27 дырок;
б) 31 дырку.
При каком наименьшем k могло такое случиться?
29. (Р. Женодаров) Все натуральные делители натурального числа d занумеровали в порядке возрастания: d1 < d2 < d3 < ... . Оказалось, что d4 + d6 + d7 = d. Найдите число d (перечислите все возможности).
30. (О. Крижановский) Имеется двадцать одинаковых на вид монет, из которых семнадцать весят по 10 г, одна - 9,9 г и две - по 9,8 г. Можно ли за два взвешивания на чашечных весах без гирь выявить хотя бы одну десятиграммовую монету?
31. (А. Шаповалов)
а) На каждой из шести карточек написано по числу. Для каждого из 63
непустых наборов этих карточек нашли сумму всех чисел, написанных на карточках
этого набора. Известно, что не все эти суммы оказались целыми. Докажите, что
целых сумм не более 31.
б) На каждой из десяти карточек написано по числу. Для каждого из 1023
непустых наборов этих карточек нашли сумму всех чисел, написанных на карточках
этого набора. Известно, что не все эти суммы оказались целыми. Сколько среди
них, самое большее, могли оказаться целыми?
32. (И. Рубанов)
а) На луче, исходящем из центра окружности K, вне окружности лежат
точки A и B, причем точка A - дальше от ее центра, чем
точка B. Без использования тригонометрии докажите, что угол между
касательными, проведенными к окружности K из точки A, меньше угла
между касательными, проведенными к окружности K из точки B.
б) То же, но без условия что точки A и B лежат на одном луче
с центром.
33. (А. Шаповалов)
а) Три соседних озерка время от времени меняют свой уровень. Каждые два из
них связаны ручьями. Могло ли случиться так, что в 1997 году вода текла из
первого озера во второе более 2/3 времени, из второго в третье - тоже более 2/3
времени и из третьего в первое - тоже более 2/3 времени?
б) Еженощно в 12 часов в гостиницах "Интурист", "КАМАЗ" и "Татарстан"
производят подсчет постояльцев. Может ли случиться так, что в течение 1997 года
по крайней мере 2/3 ночей в "Интуристе" будет больше постояльцев, чем в
"КАМАЗе", по крайней мере 2/3 ночей в "КАМАЗе" будет больше постояльцев, чем в
"Татарстане", и по крайней мере 2/3 ночей в "Татарстане" будет больше
постояльцев, чем в "Интуристе"?
34. (А. Шаповалов) Двое ходят по очереди на доске 7*8, каждый своей ладьей. Вначале ладьи стоят в противоположных углах, а все остальные поля заполнены пешками. Каждым ходом ладья должна что-нибудь съесть - пешку или ладью противника (ладьи ходят по вертикали или горизонтали на любое расстояние, но через занятые поля не перепрыгивают). Проигрывает тот, кто не может сделать очередной ход. Кто из игроков может выиграть независимо от игры другого?
35. (О. Крижановский)
а) Окружность длины 30 м разбита на 30 одинаковых частей, а точки деления
пронумерованы по ходу часовой стрелки от 1 до 30. В 12 часов большой кузнечик
находится в точке N1, а маленький - в точке N2. Большой кузнечик прыгает по
дуге на 14 м по ходу часовой стрелки каждую нечетную секунду, а маленький - на
10 м каждую четную секунду. Сколько раз до 13 часов кузнечики обгонят один
другого?
б) Окружность длины 110 м разбита на 110 одинаковых частей, а точки деления
пронумерованы по ходу часовой стрелки от 1 до 110. В 12 часов большой кузнечик
находится в точке N1, а маленький - в точке N2. Большой кузнечик прыгает по
дуге на 38 м по ходу часовой стрелки каждую нечетную секунду, а маленький - на
32 м в том же направлении каждую четную секунду. Сколько раз до 13 часов
кузнечики обгонят один другого?
36. (А. Шаповалов)
а) Придумайте какой-нибудь способ разрезать квадрат на равные треугольники
и сложить из всех них два неравных квадрата.
б) Можно ли разрезать квадрат на равные треугольники и сложить из всех них
два неравных квадрата?
37. (И. Рубанов) На складе лежат в большом количестве ширлы, мырлы и дырлы. Ширла состоит из пяти шашек, мырла - из семи машек, дырла - из девяти дашек. Все шашки одинаковы, машки - тоже, одинаковы и все дашки. У Васи есть чашечные весы без гирь, и он хочет за одно взвешивание узнать, что тяжелее: две шашки или машка с дашкой. К сожалению, все изделия, имеющиеся на складе - неразборные. Помогите Васе!
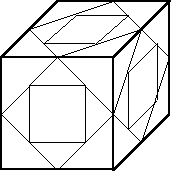
38. (А. Шаповалов) В каждый из шести квадратов, составляющих
грани куба, вписали меньший квадрат так, что его вершины попали в середины
ребер. Точно так же вписали по меньшему квадрату в каждый из новых квадратов.
Может ли муравей, двигаясь только по сторонам квадратов, обойти все вершины
всех квадратов ровно по одному разу?

39. (Р. Женодаров) Каково наибольшее возможное количество последовательных натуральных чисел, у каждого из которых ровно четыре натуральных делителя (включая единицу и само число)?
40. (А. Шаповалов, Р. Женодаров) На доске 50*50 на каждой клетке одной из диагоналей стоит по шашке. Два игрока, делая ходы по очереди, играют в следующую игру. За один ход игрок сдвигает одну из шашек на одну клетку в фиксированном направлении (вниз). Если при этом шашка сходит с доски, игрок забирает ее себе в карман. Какое наибольшее количество шашек может забрать себе в карман первый игрок независимо от игры второго?
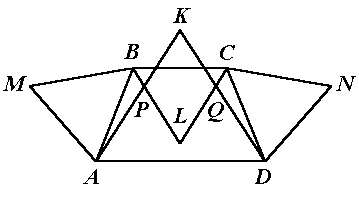
41. (С. Волченков) На боковых сторонах равнобедренной
трапеции ABCD с основаниями BC и AD построены внешним
образом равносторонние треугольники AMB и CND. На основаниях той
же трапеции внутренним образом построены еще два равносторонних треугольника
AKD и BCL. Точки P и Q - точки пересечения их
сторон, не параллельных основаниям трапеции (см. рис.). Докажите, что точки
M, P, Q и N лежат на одной прямой.
42. (А. Шаповалов)
а) На складе лежат 27 деталей, промаркированных первым или вторым сортом.
Детали одинакового сорта весят одинаково, и каждая деталь второго сорта немного
легче детали первого сорта. Известно, что ровно одна из деталей промаркирована
неправильно. Покажите, что ее можно наверняка выявить за три взвешивания на
чашечных весах без гирь.
б) То же, но из 81 детали за четыре взвешивания.
43. (А. Шаповалов) На острове Гдетотам расстояние между любыми двумя городами больше 100 км (хотя бы один город на острове есть). Местность, от которой до ближайшего гдетотамского города больше 40 км, считается провинцией. Раньше более 90% территории Гдетотама было провинцией, пока на этом острове не был построен еще один город. Может ли теперь провинция составлять менее 10% территории Гдетотама?
44. (А. Шаповалов) По итогам математической карусели восьми командам раздали 97 лотерейных билетов. За более высокое место давали больше билетов. Известно, что все команды получили разное число билетов, причем первая команда получила меньше, чем две последние вместе. Сколько билетов получила каждая из восьми команд?
45. (Илья Богданов) По кругу расставлены десять чисел. Известно, что квадрат любого из них равен произведению этого числа на сумму двух соседних. Докажите, что какие-то два соседних числа равны нулю.
46. (А. Шаповалов) Докажите (не используя длинного перебора), что нельзя отметить ровно по одной букве в каждом из слов данной задачи так, чтобы среди отмеченных букв не было бы повторяющихся.
47. (Р. Женодаров) Есть два бумажных прямоугольных треугольника: красный с углами 30o и 60o и зеленый - с углами по 45o. Эти треугольники разрезали на n меньших треугольников каждый и разложили парами: красный с зеленым. При каком наименьшем n может случиться так, что в каждой паре набор углов красного треугольника совпадает с набором углов зеленого треугольника?
48. (А. Шаповалов) Киса Воробьянинов попросил Остапа Бендера поменять в банке некоторое количество долларов на рубли по курсу 5900 рублей за доллар. Остап нашел банк, в котором, начиная с 1000 долларов, курс покупки выше. Взяв у Корейко в долг доллары, недостающие до 1000, он поменял 1000 долларов по курсу 6000 рублей за доллар и купил по курсу 6100 рублей за доллар столько же долларов, сколько занимал. Когда Остап вернул долг Корейко и отдал Воробьянинову причитающееся количество рублей, прибыль от этой операции составила 50000 рублей. Сколько долларов Киса дал Остапу для обмена
49. (А. Шаповалов) Клетчатый квадрат 1997*1997 разрезали на несколько прямоугольников (по границам клеток). Докажите, что среди них найдется прямоугольник, периметр которого кратен четырем.
50. (К. Кноп) На столе лежали шесть монет. Известно, что три из них - настоящие (весящие одинаково), а три других - фальшивые (также весящие одинаково), более легкие, чем настоящие. Вася принес с собой еще одну монету (одного из двух описанных типов). За какое наименьшее число взвешиваний на чашечных весах без гирь он сможет наверняка выяснить, настоящая это монета или фальшивая?
51. (А. Шаповалов) Шахматная доска покрыта 32 домино (каждое домино покрывает ровно два поля). Докажите, что эти домино можно так повернуть на 90o или на 180o (каждое - вокруг центра одной из закрываемых им клеток), чтобы по-прежнему вся доска была покрыта.
52. (А. Шаповалов) Все натуральные числа от 1 до 6000 записали в новом порядке: сначала выписали все четные по возрастанию (то есть 2, 4, 6, ...), затем - все оставшиеся, кратные трем, также по возрастанию, затем - все оставшиеся, кратные пяти (по возрастанию), и т.д. Какое число оказалось на 4004-м месте?
53. (А. Шаповалов) Из шахматной доски вырезан прямоугольник со сторонами, параллельными ее краям (стороны не обязательно идут по границам клеток). Докажите, что разность площадей белой и черной его частей не превосходит площади одной клетки.
54. (Р. Женодаров) В треугольнике ABC угол A равен 60o, а угол B равен 45o. На продолжении CA за точку A взята точка K такая, что AK=AС/2. Найдите величину угла ABK.
55. (Р. Женодаров и др.) На стороне AB треугольника ABC взята точка D, равноудаленная от вершин B и C. На продолжении CA за точку A взята точка K такая, что AK = AD. Известно, что угол ACD равен 36o, а угол CAD равен 72o. Найдите величину угла ABK.
56. (К. Кноп)
а) Десять команд сыграли однокруговой футбольный турнир, причем некоторые
игры завершились вничью. Оказалось, что ни для какой тройки команд количество
ничьих среди трех сыгранных ими между собой матчей не равно одному. Какое
наименьшее число матчей в этом турнире могло закончиться вничью?
б) Десять команд сыграли однокруговой футбольный турнир, причем не все игры
завершились вничью. Оказалось, что ни для какой тройки команд количество ничьих
среди трех сыгранных ими между собой матчей не равно двум. Какое наибольшее
число матчей в этом турнире могло закончиться вничью?
57. (А. Шаповалов) Может ли сумма восьми натуральных чисел (не обязательно различных) быть на восемь больше их произведения?
58. (А. Шаповалов)
а) Имеется кучка из 97 орехов. За одну
операцию разрешается любую из имеющихся кучек разделить на две. При этом, если
образовались две неравные кучки, то взимается штраф один рубль. Какова
наименьшая возможная сумма штрафа, которую приходится заплатить, чтобы получить
97 кучек, по одному ореху в каждой?
б) То же, но всюду 1997 вместо 97?
59. (А. Шаповалов) Имеется кучка из 97 орехов. Два игрока, делая ходы по очереди, играют в следующую игру. За один ход игрок делит любую из имеющихся кучек на две. При этом, если образовались две неравные кучки, то он проигрывает сопернику один рубль. Игра заканчивается, когда в каждой кучке окажется по одному ореху. Может ли кто-нибудь из игроков обеспечить себе выигрыш независимо от игры соперника?
60. (А. Шаповалов) Можно ли разрезать единичный квадрат на пять прямоугольников периметра 2 (не обязательно одинаковых)?
61. (А. Шаповалов) Представьте число 1997 в виде суммы наибольшего возможного количества натуральных слагаемых, все цифры которых различны (в совокупности).
62. (Р. Садыков, О. Крижановский, К. Кноп) Остап Бендер организовал раздачу слонов населению. Явилось двадцать человек. Остап построил их по кругу, дал одному первого слона, его соседу слева - второго, затем одного человека пропустил, следующему дал слона, пропустил двоих, следующему дал слона и т.д., пока не раздал всех 1997 имеющихся у него слонов. Скольким желающим не досталось ни одного слона?
63. (Р. Женодаров, А. Шаповалов) Можно ли разрезать квадрат на двадцать шесть прямоугольников так, чтобы каждый из них граничил по отрезку ровно с четырьмя другими?
64. (А. Шаповалов) Гата и Толя сыграли партию в шахматы. Белые пожертвовали ферзя и в итоге поставили мат одинокому черному королю. Докажите, что в партии был момент, когда число съеденных черных фигур и пешек равнялось числу белых фигур и пешек на доске.