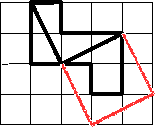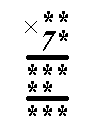
Правила "Математической карусели" приведены здесь.
Скачать zip-архив этой страницы с рисунками (mkarus13.zip)
Скачать zip-архив файла в формате WinWord kar13.doc (kar13.zip) с этой же информацией.
1. Из А в В вышел путник. Одновременно с ним из В в А вышел второй путник. Оба они шли равномерно, но с разными скоростями. В момент встречи первому оставалось идти еще 36 минут, а второму - 25 минут. Через сколько минут после выхода они встретились ?
2. Найдите все пары натуральных чисел х, у такие, что 2х+1 делится на у, а 2у+1 делится на х.
3. Из двух одинаковых железных проволок кузнец сковал по одной цепи. Первая содержит 80 одинаковых звеньев, а вторая - 100. Каждое звено первой цепи на 5 грамм тяжелее каждого звена второй цепи. Какова была масса каждой проволоки?
4. Найдите три простых числа, если одно из них равно разности кубов двух других.
5. Вчера число учеников, присутствующих в классе, было в 8 раз больше числа отсутствующих. Сегодня не пришли еще два ученика, и оказалось, что отсутствуют 20% от числа учеников, присутствующих в классе. Сколько учеников в классе?
6. Найдите наименьшее натуральное число n такое, что в любом множестве из n натуральных чисел найдутся два числа, сумма или разность которых делится на 7.
7. 10 игроков играли в теннис. Проигравший игру обижался и уходил. Какое наибольшее число теннисистов могло выиграть по две партии?.
8. Расшифруйте пример на умножение (звездочками обозначены цифры):
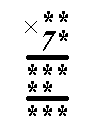
9. Урожай фруктов в этом году был отличный. Мы наварили несколько банок варенья. Я расставил их на трех полках в погребе так, чтобы на каждой полке стояло одинаковое количество литров варенья. На первую полку я поставил одну большую и четыре средних банки, на вторую - две большие и шесть литровых банок, а на третью одну большую, три средних и три литровых банки. Сколько литров варенья мы сварили?
10. Расставьте числа a=245, b=336, c=427, d=518 в порядке убывания.
11. Расставьте в записи 4*12+18:6+3 скобки так, чтобы получился наименьший возможный результат.
12. К числу 1999 припишите по цифре слева и справа так, чтобы полученное шестизначное число делилось на 33.
13. Первая цифра трехзначного числа равна 4. Если ее перенести в конец, получится число, составляющее 3/4 от исходного. Найдите исходное число.
14. Обезьяны несли Маугли орехи. По дороге они поссорились, и каждая обезьяна бросила в каждую по ореху. В результате Маугли досталось только 103 ореха. Известно, что каждая обезьяна несла одинаковое количество орехов. Сколько?
15. Найдите наибольший общий делитель чисел А=22001-1 и В=21998-1.
1. Найдите значение выражения 19992-19982+19972-...-22+12.
2. Когда Коля был молод, как Оля, много лет было тетушке Поле - годом меньше, чем Коле теперь вместе с Олей. Сколько лет было Коле, когда тетушка Поля была в возрасте Коли?
3. Найдите значение выражения x2+y2+z2, если x+y+z=1, а (1/x)+(1/y)+(1/z)=0 .
4. У меня дома есть три ведра, каждое из которых вмещает целое число литров. Если вылить полное первое ведро во второе, то вода займет там ровно 2/3 его объема, а если вылить полное первое ведро в третье, то вода займет 3/4 его объема. Однажды я наполнял водой тридцатилитровую бочку, сначала вылив первое ведро, потом второе, затем третье ведро, но бочка еще не наполнилась. Сколько литров воды можно было еще в нее влить?
5. Найдите все решения ребуса (ПАР)2=АХАХА
6. На шахматной доске стоят 10 шахматных фигур (слоны и ладьи), не бьющих друг друга. Какое наименьшее количество слонов может быть среди них?
7. Номера каких годов XX века могут быть представлены в виде 2n-2k, где n и k - натуральные числа?
8. В треугольнике АВС средняя по величине сторона отличается от каждой из остальных сторон на 1см. Найдите эти стороны, если известно, что биссектриса угла С пересекается с медианой угла В под прямым углом.
9. Число БАОБАБ делится на 101. Какое это число?
10. Найдите наименьшее натуральное число, сумма цифр которого делится на 17, и сумма цифр следующего за ним числа тоже делится на 17.
11. В треугольнике АВС стороны АВ и ВС равны 2, а высота, опущенная из вершины А, равна 1. Какими могут быть углы треугольника?
12. Положительное число А больше числа В в n раз, а сумма чисел А и В больше их разности в m раз. Чему может быть равна сумма m+n, если числа m и n - натуральные?
13. Число 6116 обладает таким свойством: как бы ни разбить его цифры на две пары, сумма цифр из первой пары оканчивается на ту же цифру, что и сумма цифр из второй пары. А сколько всего четырехзначных чисел с таким свойством?
14. На столе лежали три карточки с различными цифрами. Сначала из них сложили наибольшее возможное трехзначное число, а потом - следующее по величине. Их сумма оказалась равной 1233. Какие цифры могли быть на карточках?
15. Найдите минимальное натуральное число, которое можно двумя различными способами представить в виде 13a+31b, где a и a - натуральные числа.
16. Из горячего крана ванна заполняется за 23 минуты, из холодного - за 17 минут. Маша открыла сначала горячий кран. Через сколько минут она должна открыть холодный, чтобы к моменту наполнения ванны горячей воды налилось в 1,5 раза больше, чем холодной?
17. На какое минимальное число квадратов (не обязательно равных) можно разрезать прямоугольник размером 5*6?
18. Найдите все такие двузначные числа А, для каждого из
которых верны ровно два из следующих четырех условий:
1) А делится на 5;
2) А делится на 23;
3) А+7 - квадрат целого числа;
4) А-10 - квадрат целого числа.
19. Найдите все пары натуральных чисел, сумма квадратов которых равна 5997.
20. Все стенки и дно картонной коробки (без крышки) представляют собой квадраты площадью 1. Разрежьте коробку на три куска так, чтобы из них можно было сложить квадрат площадью 5.